苏教版(2019)高中数学必修第二册 10.1.3_两角和与差的正切公式_课件(共23张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 10.1.3_两角和与差的正切公式_课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1002.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 21:51:57 | ||
图片预览








文档简介
(共23张PPT)
10.1.3 两角和与差的正切公式
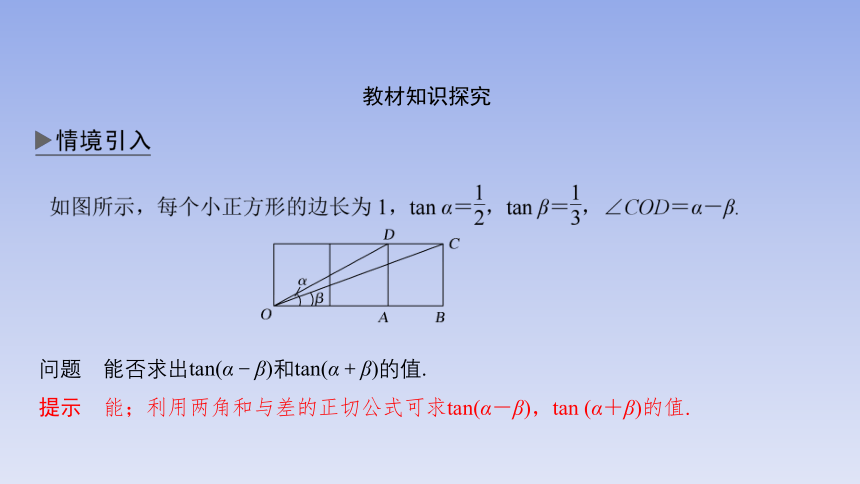
教材知识探究
问题 能否求出tan(α-β)和tan(α+β)的值.
提示 能;利用两角和与差的正切公式可求tan(α-β),tan (α+β)的值.
两角和与差的
正切公式
注意公式中的符号
[微思考]
你能借助两角和与差的正、余弦公式推导tan(α+β)与tan(α-β)吗?
=( )
答案 A
tan β
答案 -1
tan α+tan β=tan(α+β)(1-tan αtan β)得:
tan 10°+tan 35°=tan 45°(1-tan 10°tan 35°)
=1-tan 10°tan 35,
所以tan 10°+tan 35°+tan 10°tan 35°=1.
(3)(1+tan 18°)(1+tan 27°)=1+tan 18°+tan 27°+tan 18°tan 27°=1+tan 45°(1-tan 18°tan 27°)+tan 18°·tan 27°=2.
题型二 条件求值问题
【例2】 (1)设tan α,tan β是方程x2-3x+2=0的根,则tan(α+β)的值为( )
A.-3 B.-1
C.1 D.3
答案 A
答案 C
规律方法 给值求值问题的两种变换
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系以实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角与待求角间的关系,如用α=β-(β-α),2α=(α+β)+(α-β)等关系,把待求的三角函数与已知三角函数巧妙地建立等量关系,从而求值.
题型三 给值求角问题
【例3】 (1)
在△ABC中,
(2)若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.
解 ∵(1-tan α)(1-tan β)=2,
∴1-(tan α+tan β)+tan αtan β=2,
∴tan α+tan β=tan αtan β-1,
规律方法 探究利用公式T(α±β)求角的步骤
(1)求值:根据题设条件求角的某一三角函数值.
(2)确定所求角的范围(范围讨论的过大或过小,会使求出的角不合题意或漏解),根据范围找出角.
答案 C
解析 ①②③恒成立.
答案 B
答案 C
10.1.3 两角和与差的正切公式
教材知识探究
问题 能否求出tan(α-β)和tan(α+β)的值.
提示 能;利用两角和与差的正切公式可求tan(α-β),tan (α+β)的值.
两角和与差的
正切公式
注意公式中的符号
[微思考]
你能借助两角和与差的正、余弦公式推导tan(α+β)与tan(α-β)吗?
=( )
答案 A
tan β
答案 -1
tan α+tan β=tan(α+β)(1-tan αtan β)得:
tan 10°+tan 35°=tan 45°(1-tan 10°tan 35°)
=1-tan 10°tan 35,
所以tan 10°+tan 35°+tan 10°tan 35°=1.
(3)(1+tan 18°)(1+tan 27°)=1+tan 18°+tan 27°+tan 18°tan 27°=1+tan 45°(1-tan 18°tan 27°)+tan 18°·tan 27°=2.
题型二 条件求值问题
【例2】 (1)设tan α,tan β是方程x2-3x+2=0的根,则tan(α+β)的值为( )
A.-3 B.-1
C.1 D.3
答案 A
答案 C
规律方法 给值求值问题的两种变换
(1)式子的变换:分析已知式子的结构特点,结合两角和与差的三角函数公式,通过变形,建立与待求式间的联系以实现求值.
(2)角的变换:首先从已知角间的关系入手,分析已知角与待求角间的关系,如用α=β-(β-α),2α=(α+β)+(α-β)等关系,把待求的三角函数与已知三角函数巧妙地建立等量关系,从而求值.
题型三 给值求角问题
【例3】 (1)
在△ABC中,
(2)若α,β均为钝角,且(1-tan α)(1-tan β)=2,求α+β.
解 ∵(1-tan α)(1-tan β)=2,
∴1-(tan α+tan β)+tan αtan β=2,
∴tan α+tan β=tan αtan β-1,
规律方法 探究利用公式T(α±β)求角的步骤
(1)求值:根据题设条件求角的某一三角函数值.
(2)确定所求角的范围(范围讨论的过大或过小,会使求出的角不合题意或漏解),根据范围找出角.
答案 C
解析 ①②③恒成立.
答案 B
答案 C
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
