苏教版(2019)高中数学必修第二册 第10章_10.1.2_两角和与差的正弦_课件(共69张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 第10章_10.1.2_两角和与差的正弦_课件(共69张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 00:00:00 | ||
图片预览





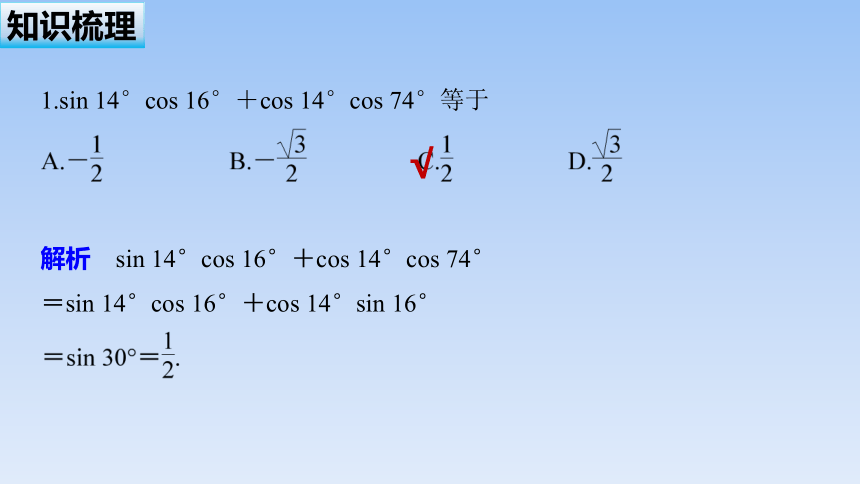


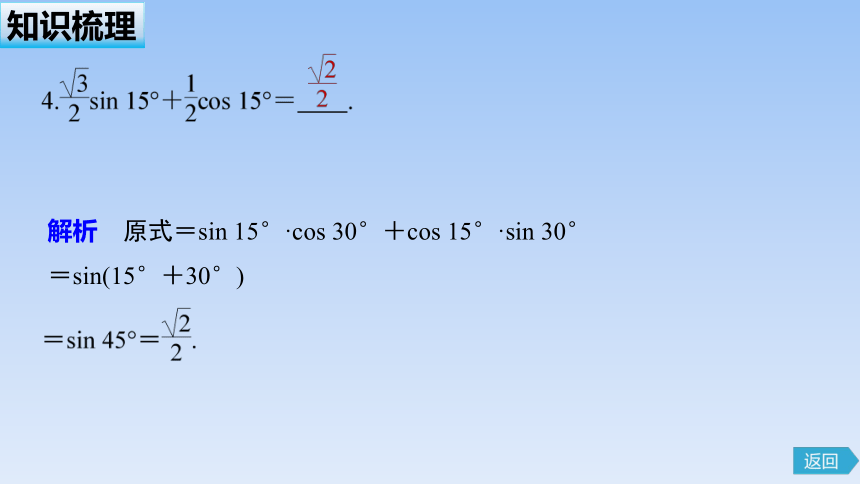


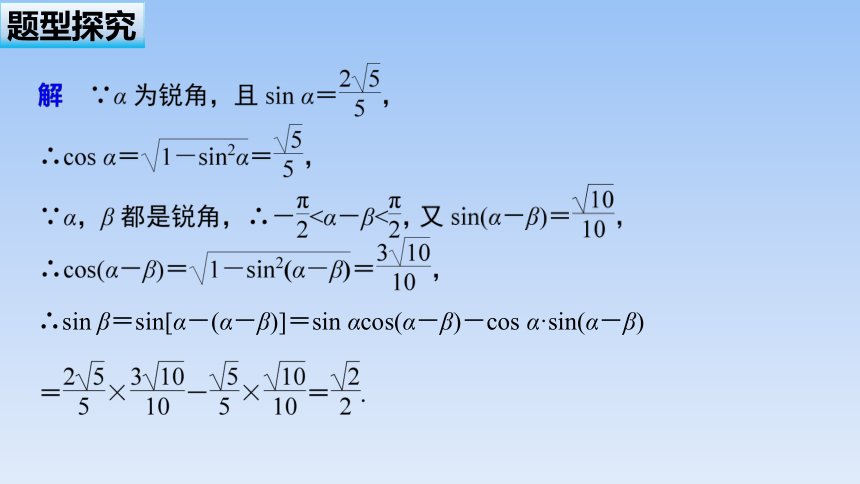
文档简介
(共69张PPT)
10.1.2 两角和与差的正弦
第十章 10.1 两角和与差的三角函数
1.了解两角和与差的正弦和两角和与差的余弦间的关系.
2.会推导两角和与差的正弦公式,掌握公式的特征.
3.能运用公式进行三角函数的有关化简求值.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点 两角和与差的正弦
名称 简记符号 公式 使用条件
两角和的正弦 S(α+β) sin(α+β)=___________ __________ α,β∈R
两角差的正弦 S(α-β) sin(α-β)=sin αcos β-cos αsin β α,β∈R
sin αcos β+
cos αsin β
记忆口诀:“正余余正,符号相同”.
知识梳理
1.sin 14°cos 16°+cos 14°cos 74°等于
解析 sin 14°cos 16°+cos 14°cos 74°
=sin 14°cos 16°+cos 14°sin 16°
√
知识梳理
知识梳理
知识梳理
解析 原式=sin 15°·cos 30°+cos 15°·sin 30°
=sin(15°+30°)
知识梳理
2
题型探究
PART TWO
一、给值(式)求值
题型探究
∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos α·sin(α-β)
题型探究
题型探究
∴sin 2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
题型探究
题型探究
给值(式)求值的策略
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式.
(2)当“已知角”有一个时,此时应着眼于“所求角”或特殊角与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.
反思感悟
√
题型探究
题型探究
题型探究
二、给值求角
题型探究
所以sin β=sin[(α+β)-α]
=sin(α+β)cos α-cos(α+β)sin α
题型探究
解决给值求角问题的方法
解决此类题目的关键是求出所求角的某一三角函数值,而三角函数的选取一般要根据所求角的范围来确定,当所求角的范围
反思感悟
题型探究
解 因为α,β均为锐角,
所以sin(α-β)=sin αcos β-cos αsin β
题型探究
三、两角和与差的正弦、余弦公式的应用
例3 (1)(多选)f(x)=sin 2x-cos 2x,则f(x)在下列区间上是增函数的是
√
√
题型探究
解析 f(x)=sin 2x-cos 2x
经检验B,C正确.
题型探究
[-1,3]
∴-2≤m-1≤2,即-1≤m≤3.
题型探究
(1)对形如sin α±cos α, sin α±cos α的三角函数式均可利用特殊角的关系,运用和、差角正弦、余弦公式化简为含一个三角函数式的形式,即y=Asin(α+φ)的形式.
反思感悟
(2)辅助角公式
反思感悟
√
题型探究
题型探究
两角和与差的正弦的证明问题
证明 对任意α,β∈R,sin(α+β)=sin αcos β+cos αsin β,
sin(α-β)=sin αcos β-cos αsin β,
两式相加,得sin(α+β)+sin(α-β)=2sin αcos β,
题型探究
=sin(α+β)cos α-cos(α+β)sin α=sin(α+β-α)
=sin β=右边.
∴原等式成立.
题型探究
(1)证明三角恒等式的方法
①从较复杂的一边证向较简单的一边;
②从两边着手,证明等式的左、右两边等于同一个数或式子;
(2)通过两角和与差的正弦公式的变形应用,培养逻辑推理的核心素养.
反思感悟
3
随堂演练
PART THREE
1.sin 7°cos 37°-sin 83°sin 37°的值为
1
2
3
4
5
√
解析 原式=sin 7°cos 37°-cos 7°sin 37°=sin(-30°)
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
随堂演练
1.知识清单:
(1)公式的推导.
(2)给式求值、给值求值、给值求角.
(3)公式的正用、逆用、变形用.
2.方法归纳:构造法.
3.常见误区:求值或求角时忽略角的范围.
课堂小结
4
课时对点练
PART FOUR
1.sin 40°cos 10°-sin 130°sin 10°等于
√
解析 sin 40°cos 10°-sin 130°sin 10°
=sin 40°cos 10°-cos 40°sin 10°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)为奇函数.
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以cos(α+β)=cos αcos β-sin αsin β
sin(α+β)=sin αcos β+cos αsin β
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-1
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=2sin(15°-45°)
=2sin(-30°)
=-1.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)= .
解析 ∵sin α+cos β=1,cos α+sin β=0,
∴sin2α+cos2β+2sin αcos β=1, ①
cos2α+sin2β+2cos αsin β=0, ②
①②两式相加可得sin2α+cos2α+sin2β+cos2β+2(sin αcos β+cos αsin β)=1,
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
11.在△ABC中,如果sin A=2sin Ccos B,那么这个三角形是
A.锐角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵A+B+C=π,∴A=π-(B+C),
由已知可得sin(B+C)=2sin Ccos B
sin Bcos C+cos Bsin C=2sin Ccos B
sin Bcos C-cos Bsin C=0 sin(B-C)=0.
∵0∴-π∴B=C.故△ABC为等腰三角形.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴sin αcos β=cos α+cos αsin β,
综合运用
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,在边长为1的正方形ABCD中,P,Q分别为边BC,CD上的点,且△PCQ的周长为2,则线段PQ长度的最小值是 .
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则CP=PQcos θ,CQ=PQsin θ,又△PCQ的周长为2,
综合运用
15.在△ABC中,3sin A+4cos B=6,3cos A+4sin B=1,则C的大小为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
拓广探究
①
②
①2+②2得9+16+24sin(A+B)=37.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求函数f(x)的最小正周期;
拓广探究
(2)求函数f(x)的对称轴和对称中心.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
10.1.2 两角和与差的正弦
第十章 10.1 两角和与差的三角函数
1.了解两角和与差的正弦和两角和与差的余弦间的关系.
2.会推导两角和与差的正弦公式,掌握公式的特征.
3.能运用公式进行三角函数的有关化简求值.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点 两角和与差的正弦
名称 简记符号 公式 使用条件
两角和的正弦 S(α+β) sin(α+β)=___________ __________ α,β∈R
两角差的正弦 S(α-β) sin(α-β)=sin αcos β-cos αsin β α,β∈R
sin αcos β+
cos αsin β
记忆口诀:“正余余正,符号相同”.
知识梳理
1.sin 14°cos 16°+cos 14°cos 74°等于
解析 sin 14°cos 16°+cos 14°cos 74°
=sin 14°cos 16°+cos 14°sin 16°
√
知识梳理
知识梳理
知识梳理
解析 原式=sin 15°·cos 30°+cos 15°·sin 30°
=sin(15°+30°)
知识梳理
2
题型探究
PART TWO
一、给值(式)求值
题型探究
∴sin β=sin[α-(α-β)]=sin αcos(α-β)-cos α·sin(α-β)
题型探究
题型探究
∴sin 2α=sin[(α-β)+(α+β)]
=sin(α-β)cos(α+β)+cos(α-β)sin(α+β)
题型探究
题型探究
给值(式)求值的策略
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式.
(2)当“已知角”有一个时,此时应着眼于“所求角”或特殊角与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.
反思感悟
√
题型探究
题型探究
题型探究
二、给值求角
题型探究
所以sin β=sin[(α+β)-α]
=sin(α+β)cos α-cos(α+β)sin α
题型探究
解决给值求角问题的方法
解决此类题目的关键是求出所求角的某一三角函数值,而三角函数的选取一般要根据所求角的范围来确定,当所求角的范围
反思感悟
题型探究
解 因为α,β均为锐角,
所以sin(α-β)=sin αcos β-cos αsin β
题型探究
三、两角和与差的正弦、余弦公式的应用
例3 (1)(多选)f(x)=sin 2x-cos 2x,则f(x)在下列区间上是增函数的是
√
√
题型探究
解析 f(x)=sin 2x-cos 2x
经检验B,C正确.
题型探究
[-1,3]
∴-2≤m-1≤2,即-1≤m≤3.
题型探究
(1)对形如sin α±cos α, sin α±cos α的三角函数式均可利用特殊角的关系,运用和、差角正弦、余弦公式化简为含一个三角函数式的形式,即y=Asin(α+φ)的形式.
反思感悟
(2)辅助角公式
反思感悟
√
题型探究
题型探究
两角和与差的正弦的证明问题
证明 对任意α,β∈R,sin(α+β)=sin αcos β+cos αsin β,
sin(α-β)=sin αcos β-cos αsin β,
两式相加,得sin(α+β)+sin(α-β)=2sin αcos β,
题型探究
=sin(α+β)cos α-cos(α+β)sin α=sin(α+β-α)
=sin β=右边.
∴原等式成立.
题型探究
(1)证明三角恒等式的方法
①从较复杂的一边证向较简单的一边;
②从两边着手,证明等式的左、右两边等于同一个数或式子;
(2)通过两角和与差的正弦公式的变形应用,培养逻辑推理的核心素养.
反思感悟
3
随堂演练
PART THREE
1.sin 7°cos 37°-sin 83°sin 37°的值为
1
2
3
4
5
√
解析 原式=sin 7°cos 37°-cos 7°sin 37°=sin(-30°)
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
随堂演练
1
2
3
4
5
随堂演练
1.知识清单:
(1)公式的推导.
(2)给式求值、给值求值、给值求角.
(3)公式的正用、逆用、变形用.
2.方法归纳:构造法.
3.常见误区:求值或求角时忽略角的范围.
课堂小结
4
课时对点练
PART FOUR
1.sin 40°cos 10°-sin 130°sin 10°等于
√
解析 sin 40°cos 10°-sin 130°sin 10°
=sin 40°cos 10°-cos 40°sin 10°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
A.奇函数 B.偶函数
C.既是奇函数又是偶函数 D.非奇非偶函数
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴f(x)为奇函数.
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以cos(α+β)=cos αcos β-sin αsin β
sin(α+β)=sin αcos β+cos αsin β
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
-1
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
=2sin(15°-45°)
=2sin(-30°)
=-1.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8.已知sin α+cos β=1,cos α+sin β=0,则sin(α+β)= .
解析 ∵sin α+cos β=1,cos α+sin β=0,
∴sin2α+cos2β+2sin αcos β=1, ①
cos2α+sin2β+2cos αsin β=0, ②
①②两式相加可得sin2α+cos2α+sin2β+cos2β+2(sin αcos β+cos αsin β)=1,
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
11.在△ABC中,如果sin A=2sin Ccos B,那么这个三角形是
A.锐角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 ∵A+B+C=π,∴A=π-(B+C),
由已知可得sin(B+C)=2sin Ccos B
sin Bcos C+cos Bsin C=2sin Ccos B
sin Bcos C-cos Bsin C=0 sin(B-C)=0.
∵0
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴sin αcos β=cos α+cos αsin β,
综合运用
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14.如图,在边长为1的正方形ABCD中,P,Q分别为边BC,CD上的点,且△PCQ的周长为2,则线段PQ长度的最小值是 .
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
则CP=PQcos θ,CQ=PQsin θ,又△PCQ的周长为2,
综合运用
15.在△ABC中,3sin A+4cos B=6,3cos A+4sin B=1,则C的大小为
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
拓广探究
①
②
①2+②2得9+16+24sin(A+B)=37.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)求函数f(x)的最小正周期;
拓广探究
(2)求函数f(x)的对称轴和对称中心.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
