苏教版(2019)高中数学必修第二册 10.1.2_两角和与差的正弦、余弦公式_学案
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 10.1.2_两角和与差的正弦、余弦公式_学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 111.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:04:47 | ||
图片预览

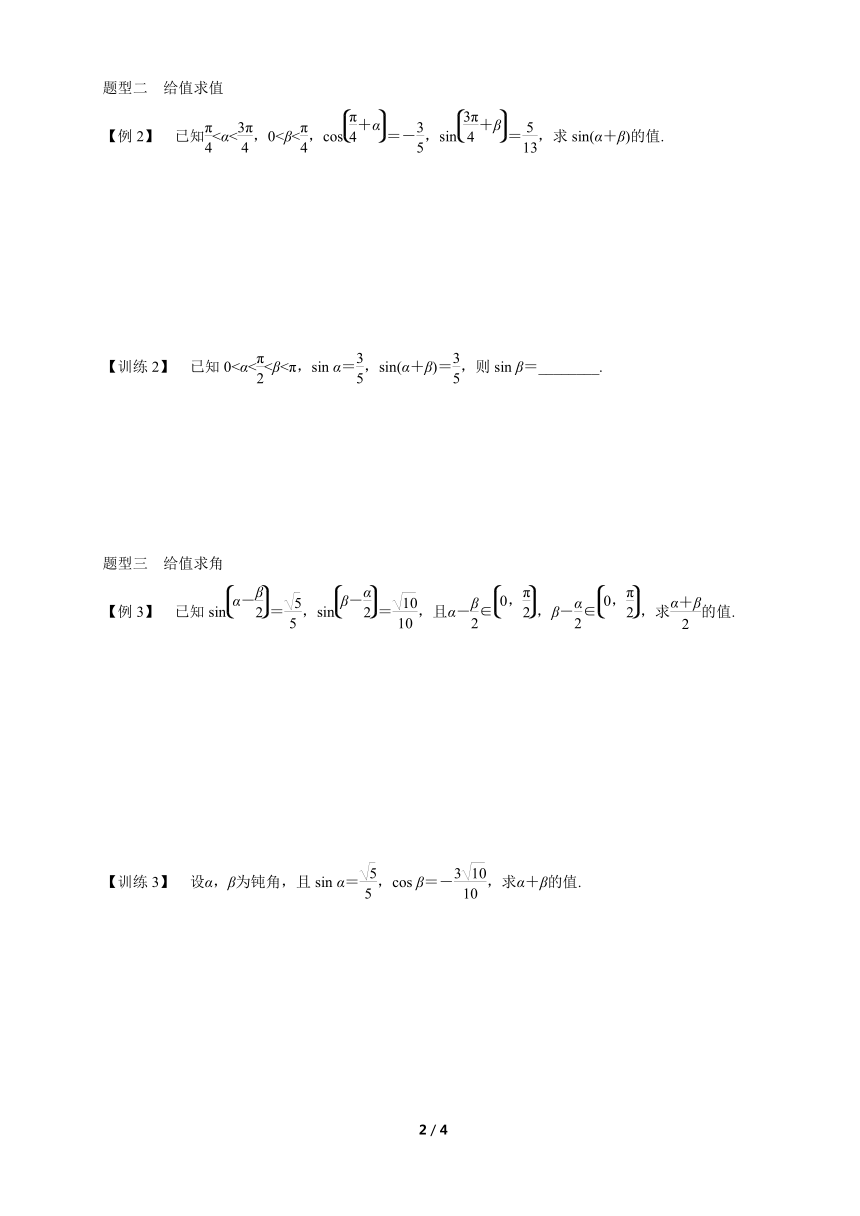
文档简介
第十章 三角恒等变换
10.1.2 两角和与差的正弦、余弦公式
1.掌握由两角差的余弦公式推导出两角和的余弦公式及两角差(和)的正弦公式.
2.会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简.
1.教学重点:会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简.
2.教学难点:掌握由两角差的余弦公式推导出两角和的余弦公式及两角差(和)的正弦公式.
题型一 公式的正用和逆用
【例1】 求值:
(1)sin 20°cos 40°+cos 20°sin 40°=________;
(2)sin 15°+sin 75°=________;
(3)已知α,β为锐角,且sin α=,sin β=,则sin(α+β)的值为________sin(α-β)的值为________.
【训练1】 (1)化简:sin 14°cos 16°+sin 76°cos 74°=________;
(2)求值:=________.
题型二 给值求值
【例2】 已知<α<,0<β<,cos=-,sin=,求sin(α+β)的值.
【训练2】 已知0<α<<β<π,sin α=,sin(α+β)=,则sin β=________.
题型三 给值求角
【例3】 已知sin=,sin=,且α-∈,β-∈,求的值.
【训练3】 设α,β为钝角,且sin α=,cos β=-,求α+β的值.
1.sin 7°cos 37°-sin 83°sin 37°的值为( )
A.- B.- C. D.
2.已知cos(α+β)=,cos(α-β)=-,则cos αcos β的值为( )
A.0 B.
C.0或 D.0或±
3.求值:cos+sin=________.
4.函数f(x)=sin x-cos x(x∈R)的值域是________.
5.化简:sincos-cos·sin.
参考答案
1. 解析 原式=sin 7°cos 37°-cos 7°sin 37°=sin(-30°)=-sin 30°=-.
答案 B
2. 解析 cos(α+β)=cos αcos β-sin αsin β=,
cos(α-β)=cos αcos β+sin αsin β=-,
两式相加可得2cos αcos β=0,即cos αcos β=0.
答案 A
3. 解析 原式=sincos+cossin=sin=sin=.
答案
4. 解析 ∵f(x)=2=2sin.
∴f(x)∈[-2,2].
答案 [-2,2]
5. 解析 原式=sin 30°sin 60°+cos 30°cos 60°
=cos(60°-30°)=cos 30°=.
答案
解 原式=sincos-sin·cos=sin
=sin=sin cos -cos sin =×-×=.
4 / 4
10.1.2 两角和与差的正弦、余弦公式
1.掌握由两角差的余弦公式推导出两角和的余弦公式及两角差(和)的正弦公式.
2.会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简.
1.教学重点:会用两角和与差的正弦、余弦公式进行简单的三角函数的求值、化简.
2.教学难点:掌握由两角差的余弦公式推导出两角和的余弦公式及两角差(和)的正弦公式.
题型一 公式的正用和逆用
【例1】 求值:
(1)sin 20°cos 40°+cos 20°sin 40°=________;
(2)sin 15°+sin 75°=________;
(3)已知α,β为锐角,且sin α=,sin β=,则sin(α+β)的值为________sin(α-β)的值为________.
【训练1】 (1)化简:sin 14°cos 16°+sin 76°cos 74°=________;
(2)求值:=________.
题型二 给值求值
【例2】 已知<α<,0<β<,cos=-,sin=,求sin(α+β)的值.
【训练2】 已知0<α<<β<π,sin α=,sin(α+β)=,则sin β=________.
题型三 给值求角
【例3】 已知sin=,sin=,且α-∈,β-∈,求的值.
【训练3】 设α,β为钝角,且sin α=,cos β=-,求α+β的值.
1.sin 7°cos 37°-sin 83°sin 37°的值为( )
A.- B.- C. D.
2.已知cos(α+β)=,cos(α-β)=-,则cos αcos β的值为( )
A.0 B.
C.0或 D.0或±
3.求值:cos+sin=________.
4.函数f(x)=sin x-cos x(x∈R)的值域是________.
5.化简:sincos-cos·sin.
参考答案
1. 解析 原式=sin 7°cos 37°-cos 7°sin 37°=sin(-30°)=-sin 30°=-.
答案 B
2. 解析 cos(α+β)=cos αcos β-sin αsin β=,
cos(α-β)=cos αcos β+sin αsin β=-,
两式相加可得2cos αcos β=0,即cos αcos β=0.
答案 A
3. 解析 原式=sincos+cossin=sin=sin=.
答案
4. 解析 ∵f(x)=2=2sin.
∴f(x)∈[-2,2].
答案 [-2,2]
5. 解析 原式=sin 30°sin 60°+cos 30°cos 60°
=cos(60°-30°)=cos 30°=.
答案
解 原式=sincos-sin·cos=sin
=sin=sin cos -cos sin =×-×=.
4 / 4
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
