苏教版(2019)高中数学必修第二册 第10章_10.2_二倍角的三角函数_课件(共59张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 第10章_10.2_二倍角的三角函数_课件(共59张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:10:58 | ||
图片预览











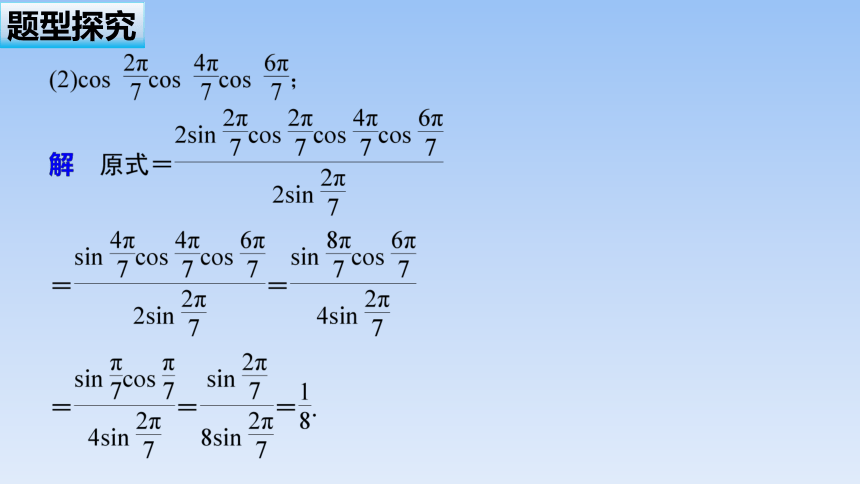
文档简介
(共59张PPT)
10.2 二倍角的三角函数
第十章 三角恒等变换
1.会用两角和(差)的正弦、余弦、正切公式推导出二倍角的正弦、
余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的三角恒等变换并能灵活地将
公式变形运用.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点 二倍角公式
1.倍角公式
(1)sin 2α= .(S2α)
(2)cos 2α= = = .(C2α)
(3)tan 2α= .(T2α)
2.二倍角公式的重要变形——升幂公式
cos 2α= -1,cos 2α=1- ,
cos α= -1,cos α=1- .
2sin αcos α
cos2α-sin2α
1-2sin2α
2cos2α-1
2cos2α
2sin2α
知识梳理
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
√
×
√
知识梳理
2
题型探究
PART TWO
一、给角求值
例1 求下列各式的值:
(1)cos 72°cos 36°;
题型探究
题型探究
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
反思感悟
跟踪训练1 求下列各式的值:
题型探究
题型探究
题型探究
二、给值求值
√
题型探究
解析 (sin α-cos α)2=sin2α+cos2α-2sin αcos α
题型探究
题型探究
(1)条件求值问题常有两种解题途径
①对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;
②对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
(2)一个重要结论:(sin θ±cos θ)2=1±sin 2θ.
反思感悟
√
题型探究
题型探究
三、利用倍角公式化简及证明
题型探究
题型探究
题型探究
三角函数式化简、证明的常用技巧
(1)特殊角的三角函数与特殊值的互化.
(2)对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分.
(3)对于二次根式,注意二倍角公式的逆用.
(4)利用角与角之间的隐含关系,如互余、互补等.
(5)利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
反思感悟
sin α-cos α
题型探究
(1)如何选择关于点O对称的点A,D的位置,可以
使矩形ABCD的面积最大,最大值是多少?
三角函数的实际应用
典例 如图,有一块以点O为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD开辟为绿地,使其一边AD落在半圆的直径上,另两点B,C落在半圆的圆周上.已知半圆的半径长为20 m.
题型探究
解 连接OB,如图所示,设∠AOB=θ,
因为A,D关于原点对称,所以AD=2OA=40cos θ.
设矩形ABCD的面积为S,则
S=AD·AB=40cos θ·20sin θ=400sin 2θ.
题型探究
(2)沿着AB,BC,CD修一条步行小路从A到D,如何选择A,D位置,使步行小路的距离最远?
题型探究
解 由(1)知AB=20sin θ,AD=40cos θ,
题型探究
三角函数与平面几何有着密切联系,几何中的角度、长度、面积等问题,常借助三角变换来解决;实际问题的意义常反映在三角形的边、角关系上,故常用建立三角函数模型解决实际的优化问题.
反思感悟
3
随堂演练
PART THREE
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
4.cos275°+cos215°+cos 75°cos 15°等于
√
解析 原式=sin215°+cos215°+sin 15°cos 15°
随堂演练
1
2
3
4
5
随堂演练
1.知识清单:
(1)二倍角公式的推导.
(2)二倍角公式的正用、逆用,利用二倍角公式进行化简和证明.
2.方法归纳:转化法.
3.常见误区:化简求值时开根号忽略角的范围导致出错.
课堂小结
4
课时对点练
PART FOUR
1.(多选)下列各式中,一定成立的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 cos4α-sin4α=(cos2α+sin2α)(cos2α-sin2α)
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.sin 6°sin 42°sin 66°sin 78°= .
解析 原式=sin 6°cos 48°cos 24°cos 12°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.求证:cos2(A+B)-sin2(A-B)=cos 2Acos 2B.
=cos 2Acos 2B=右边,所以等式成立.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
11.已知α为锐角,且满足cos 2α=sin α,则α等于
A.30°或60° B.45° C.60° D.30°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为cos 2α=1-2sin2α,
故由题意,知2sin2α+sin α-1=0,
即(sin α+1)(2sin α-1)=0.
所以α=30°.故选D.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
∵α为第二象限角,
∴cos α<0,sin α>0,cos α-sin α<0.
又∵sin α+cos α>0,
∴|cos α|<|sin α|,
∴cos 2α=cos2α-sin2α<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
A.1 B.2 C.-2 D.-4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
拓广探究
=-cos 2x-3cos x
=-2cos2x-3cos x+1,
令t=cos x,则t∈[-1,1],
∴g(t)=-2t2-3t+1,t∈[-1,1],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴当t=1时,g(t)有最小值-4.
综上,f(x)的最小值为-4.
拓广探究
(1)求sin α+cos α的值;
解 因为m与n为共线向量,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
10.2 二倍角的三角函数
第十章 三角恒等变换
1.会用两角和(差)的正弦、余弦、正切公式推导出二倍角的正弦、
余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的三角恒等变换并能灵活地将
公式变形运用.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点 二倍角公式
1.倍角公式
(1)sin 2α= .(S2α)
(2)cos 2α= = = .(C2α)
(3)tan 2α= .(T2α)
2.二倍角公式的重要变形——升幂公式
cos 2α= -1,cos 2α=1- ,
cos α= -1,cos α=1- .
2sin αcos α
cos2α-sin2α
1-2sin2α
2cos2α-1
2cos2α
2sin2α
知识梳理
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
√
×
√
知识梳理
2
题型探究
PART TWO
一、给角求值
例1 求下列各式的值:
(1)cos 72°cos 36°;
题型探究
题型探究
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
反思感悟
跟踪训练1 求下列各式的值:
题型探究
题型探究
题型探究
二、给值求值
√
题型探究
解析 (sin α-cos α)2=sin2α+cos2α-2sin αcos α
题型探究
题型探究
(1)条件求值问题常有两种解题途径
①对题设条件变形,把条件中的角、函数名向结论中的角、函数名靠拢;
②对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.
(2)一个重要结论:(sin θ±cos θ)2=1±sin 2θ.
反思感悟
√
题型探究
题型探究
三、利用倍角公式化简及证明
题型探究
题型探究
题型探究
三角函数式化简、证明的常用技巧
(1)特殊角的三角函数与特殊值的互化.
(2)对于分式形式,应分别对分子、分母进行变形处理,有公因式的提取公因式后进行约分.
(3)对于二次根式,注意二倍角公式的逆用.
(4)利用角与角之间的隐含关系,如互余、互补等.
(5)利用“1”的恒等变形,如tan 45°=1,sin2α+cos2α=1等.
反思感悟
sin α-cos α
题型探究
(1)如何选择关于点O对称的点A,D的位置,可以
使矩形ABCD的面积最大,最大值是多少?
三角函数的实际应用
典例 如图,有一块以点O为圆心的半圆形空地,要在这块空地上划出一个内接矩形ABCD开辟为绿地,使其一边AD落在半圆的直径上,另两点B,C落在半圆的圆周上.已知半圆的半径长为20 m.
题型探究
解 连接OB,如图所示,设∠AOB=θ,
因为A,D关于原点对称,所以AD=2OA=40cos θ.
设矩形ABCD的面积为S,则
S=AD·AB=40cos θ·20sin θ=400sin 2θ.
题型探究
(2)沿着AB,BC,CD修一条步行小路从A到D,如何选择A,D位置,使步行小路的距离最远?
题型探究
解 由(1)知AB=20sin θ,AD=40cos θ,
题型探究
三角函数与平面几何有着密切联系,几何中的角度、长度、面积等问题,常借助三角变换来解决;实际问题的意义常反映在三角形的边、角关系上,故常用建立三角函数模型解决实际的优化问题.
反思感悟
3
随堂演练
PART THREE
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
4.cos275°+cos215°+cos 75°cos 15°等于
√
解析 原式=sin215°+cos215°+sin 15°cos 15°
随堂演练
1
2
3
4
5
随堂演练
1.知识清单:
(1)二倍角公式的推导.
(2)二倍角公式的正用、逆用,利用二倍角公式进行化简和证明.
2.方法归纳:转化法.
3.常见误区:化简求值时开根号忽略角的范围导致出错.
课堂小结
4
课时对点练
PART FOUR
1.(多选)下列各式中,一定成立的是
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 cos4α-sin4α=(cos2α+sin2α)(cos2α-sin2α)
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7.sin 6°sin 42°sin 66°sin 78°= .
解析 原式=sin 6°cos 48°cos 24°cos 12°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9.求证:cos2(A+B)-sin2(A-B)=cos 2Acos 2B.
=cos 2Acos 2B=右边,所以等式成立.
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
11.已知α为锐角,且满足cos 2α=sin α,则α等于
A.30°或60° B.45° C.60° D.30°
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 因为cos 2α=1-2sin2α,
故由题意,知2sin2α+sin α-1=0,
即(sin α+1)(2sin α-1)=0.
所以α=30°.故选D.
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
∵α为第二象限角,
∴cos α<0,sin α>0,cos α-sin α<0.
又∵sin α+cos α>0,
∴|cos α|<|sin α|,
∴cos 2α=cos2α-sin2α<0,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
A.1 B.2 C.-2 D.-4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
拓广探究
=-cos 2x-3cos x
=-2cos2x-3cos x+1,
令t=cos x,则t∈[-1,1],
∴g(t)=-2t2-3t+1,t∈[-1,1],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
∴当t=1时,g(t)有最小值-4.
综上,f(x)的最小值为-4.
拓广探究
(1)求sin α+cos α的值;
解 因为m与n为共线向量,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
拓广探究
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
