苏教版(2019)高中数学必修第二册 第10章_10.3_几个三角恒等式_课件(共66张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 第10章_10.3_几个三角恒等式_课件(共66张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:23:26 | ||
图片预览





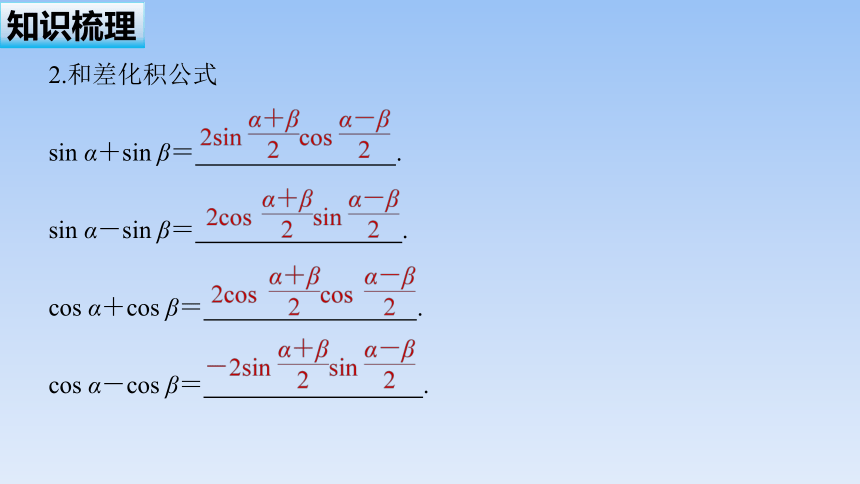





文档简介
(共66张PPT)
10.3 几个三角恒等式
第十章 三角恒等变换
1.理解积化和差、和差化积、半角公式的推导过程.
2.掌握积化和差、和差化积、半角公式的结构特征.
3.能利用所学三角公式进行三角恒等变换.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 积化和差与和差化积公式
1.积化和差公式
sin αcos β= .
cos αsin β= .
cos αcos β= .
sin αsin β= .
知识梳理
2.和差化积公式
sin α+sin β= .
sin α-sin β= .
cos α+cos β= .
cos α-cos β= .
知识梳理
知识点二 半角公式
知识梳理
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
×
知识梳理
2
题型探究
PART TWO
一、积化和差与和差化积公式的应用
例1 (1)求值:sin 20°cos 70°+sin 10°sin 50°.
解 sin 20°cos 70°+sin 10°sin 50°
题型探究
题型探究
题型探究
题型探究
(1)在运用积化和差公式时,如果形式为异名函数积时,化得的结果应为sin(α+β)与sin(α-β)的和或差;如果形式为同名函数积时,化得的结果应为cos(α+β)与cos(α-β)的和或差.
(2)和差化积公式应用时要注意只有系数的绝对值相同的各函数的和与差才能直接运用推论化成积的形式.
反思感悟
跟踪训练1 (1)化简:4sin(60°-θ)·sin θ·sin(60°+θ).
解 原式=-2sin θ·[cos 120°-cos(-2θ)]
=sin θ+2sin θcos 2θ=sin θ+sin 3θ-sin θ
=sin 3θ.
题型探究
(2)求cos 20°+cos 100°+cos 140°的值.
解 cos 20°+cos 100°+cos 140°
=2cos 60°cos 40°+cos(180°-40°)
=cos 40°-cos 40°=0.
题型探究
二、应用半角公式求值
题型探究
利用半角公式求值的思路
(1)看角:若已知三角函数式中的角是待求三角函数式中角的两倍,则求解时常常借助半角公式求解.
(2)明范围:由于半角公式求值常涉及符号问题,因此求解时务必依据角的范围,求出相应半角的范围.
反思感悟
反思感悟
题型探究
题型探究
因为α为第四象限角,所以sin α<0.
因为α为第四象限角,所以sin α<0.
题型探究
题型探究
三、三角函数式的化简
题型探究
题型探究
三角函数式化简的要求、思路和方法
(1)化简的要求:①能求出值的应求出值.②尽量使三角函数种数最少.③尽量使项数最少.④尽量使分母不含三角函数.⑤尽量使被开方数不含三角函数.
(2)化简的思路:对于和式,基本思路是降次、消项和逆用公式;对于三角分式,基本思路是分子与分母约分或逆用公式;对于二次根式,注意二倍角公式的逆用.另外,还可以用切化弦、变量代换、角度归一等方法.
反思感悟
题型探究
证明 由题意得,tan α+tan β=-3,tan α·tan β=-4,
题型探究
四、恒等式的证明
题型探究
所以原等式成立.
题型探究
三角恒等式证明的常用方法
(1)执因索果法:证明的形式一般是化繁为简.
(2)左右归一法:证明左右两边都等于同一个式子.
(3)拼凑法:针对题设和结论之间的差异,有针对性地变形,以消除它们之间的差异,简言之,即化异求同.
反思感悟
(5)分析法:从被证明的等式出发,逐步地探求使等式成立的条件,直到获得已知条件或明显的事实为止,就可以断定原等式成立.
反思感悟
题型探究
解 ∵A+B+C=180°,
题型探究
3
随堂演练
PART THREE
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
2
1
2
3
4
5
随堂演练
1
2
3
4
5
5.把下列各式化为积的形式:
(1)sin 122°+sin 36°=________________.
2sin 79°cos 43°
解析 sin 122°+sin 36°
随堂演练
1
2
3
4
5
(2)cos 75°-cos 23°=________________.
-2sin 49°sin 26°
解析 cos 75°-cos 23°
随堂演练
1.知识清单:
(1)积化和差公式.
(2)和差化积公式.
(3)半角公式.
2.方法归纳:转化与化归.
3.常见误区:半角公式符号的判断.
课堂小结
4
课时对点练
PART FOUR
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
=-2sin 54°·sin 18°=-2cos 36°cos 72°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 sin 20°+sin 40°+sin 60°-sin 80°
=2sin 30°cos 10°+sin 60°-sin 80°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
7.cos 20°sin 50°-cos 70°sin 40°=___;cos 20°+cos 100°+
cos 140°=____.
解析 cos 20°sin 50°-cos 70°sin 40°
0
cos 20°+cos 100°+cos 140°
=2cos 60°cos 40°+cos(180°-40°)
=cos 40°-cos 40°=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
8.设直角三角形中两锐角为A和B,则cos Acos B的取值范围是________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.求下列各式的值:
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)sin 138°-cos 12°+sin 54°.
解 sin 138°-cos 12°+sin 54°=sin 42°-cos 12°+sin 54°
=sin 42°-sin 78°+sin 54°=-2cos 60°sin 18°+sin 54°
=sin 54°-sin 18°=2cos 36°sin 18°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
15.已知函数f(x)=2sin(ωx+φ)(ω>0),若存在x0∈R,使得f(x0+2)-f(x0)
=4,则ω的最小值为____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
解析 4=f(x0+2)-f(x0)=2sin[ω(x0+2)+φ]
-2sin(ωx0+φ)=4sin ωcos[ω(x0+1)+φ],
所以sin ωcos[ω(x0+1)+φ]=1,
而|sin ω||cos[ω(x0+1)+φ]|≤1,
故等号成立,当且仅当|sin ω|=1,|cos[ω(x0+1)+φ]|=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
16.求函数f(x)=cos2(x+θ)-2cos θcos xcos(x+θ)+cos2θ的最小正周期、值域、单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
=1+cos(x+2θ)cos x-cos(x+2θ)cos x-cos2x
所以f(x)的最小正周期T=π,值域为[0,1],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
10.3 几个三角恒等式
第十章 三角恒等变换
1.理解积化和差、和差化积、半角公式的推导过程.
2.掌握积化和差、和差化积、半角公式的结构特征.
3.能利用所学三角公式进行三角恒等变换.
学习目标
内
容
索
引
知识梳理
题型探究
随堂演练
课时对点练
1
知识梳理
PART ONE
知识点一 积化和差与和差化积公式
1.积化和差公式
sin αcos β= .
cos αsin β= .
cos αcos β= .
sin αsin β= .
知识梳理
2.和差化积公式
sin α+sin β= .
sin α-sin β= .
cos α+cos β= .
cos α-cos β= .
知识梳理
知识点二 半角公式
知识梳理
思考辨析 判断正误
SI KAO BIAN XI PAN DUAN ZHENG WU
√
×
×
知识梳理
2
题型探究
PART TWO
一、积化和差与和差化积公式的应用
例1 (1)求值:sin 20°cos 70°+sin 10°sin 50°.
解 sin 20°cos 70°+sin 10°sin 50°
题型探究
题型探究
题型探究
题型探究
(1)在运用积化和差公式时,如果形式为异名函数积时,化得的结果应为sin(α+β)与sin(α-β)的和或差;如果形式为同名函数积时,化得的结果应为cos(α+β)与cos(α-β)的和或差.
(2)和差化积公式应用时要注意只有系数的绝对值相同的各函数的和与差才能直接运用推论化成积的形式.
反思感悟
跟踪训练1 (1)化简:4sin(60°-θ)·sin θ·sin(60°+θ).
解 原式=-2sin θ·[cos 120°-cos(-2θ)]
=sin θ+2sin θcos 2θ=sin θ+sin 3θ-sin θ
=sin 3θ.
题型探究
(2)求cos 20°+cos 100°+cos 140°的值.
解 cos 20°+cos 100°+cos 140°
=2cos 60°cos 40°+cos(180°-40°)
=cos 40°-cos 40°=0.
题型探究
二、应用半角公式求值
题型探究
利用半角公式求值的思路
(1)看角:若已知三角函数式中的角是待求三角函数式中角的两倍,则求解时常常借助半角公式求解.
(2)明范围:由于半角公式求值常涉及符号问题,因此求解时务必依据角的范围,求出相应半角的范围.
反思感悟
反思感悟
题型探究
题型探究
因为α为第四象限角,所以sin α<0.
因为α为第四象限角,所以sin α<0.
题型探究
题型探究
三、三角函数式的化简
题型探究
题型探究
三角函数式化简的要求、思路和方法
(1)化简的要求:①能求出值的应求出值.②尽量使三角函数种数最少.③尽量使项数最少.④尽量使分母不含三角函数.⑤尽量使被开方数不含三角函数.
(2)化简的思路:对于和式,基本思路是降次、消项和逆用公式;对于三角分式,基本思路是分子与分母约分或逆用公式;对于二次根式,注意二倍角公式的逆用.另外,还可以用切化弦、变量代换、角度归一等方法.
反思感悟
题型探究
证明 由题意得,tan α+tan β=-3,tan α·tan β=-4,
题型探究
四、恒等式的证明
题型探究
所以原等式成立.
题型探究
三角恒等式证明的常用方法
(1)执因索果法:证明的形式一般是化繁为简.
(2)左右归一法:证明左右两边都等于同一个式子.
(3)拼凑法:针对题设和结论之间的差异,有针对性地变形,以消除它们之间的差异,简言之,即化异求同.
反思感悟
(5)分析法:从被证明的等式出发,逐步地探求使等式成立的条件,直到获得已知条件或明显的事实为止,就可以断定原等式成立.
反思感悟
题型探究
解 ∵A+B+C=180°,
题型探究
3
随堂演练
PART THREE
1
2
3
4
5
√
随堂演练
1
2
3
4
5
√
随堂演练
1
2
3
4
5
随堂演练
2
1
2
3
4
5
随堂演练
1
2
3
4
5
5.把下列各式化为积的形式:
(1)sin 122°+sin 36°=________________.
2sin 79°cos 43°
解析 sin 122°+sin 36°
随堂演练
1
2
3
4
5
(2)cos 75°-cos 23°=________________.
-2sin 49°sin 26°
解析 cos 75°-cos 23°
随堂演练
1.知识清单:
(1)积化和差公式.
(2)和差化积公式.
(3)半角公式.
2.方法归纳:转化与化归.
3.常见误区:半角公式符号的判断.
课堂小结
4
课时对点练
PART FOUR
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
=-2sin 54°·sin 18°=-2cos 36°cos 72°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
√
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
解析 sin 20°+sin 40°+sin 60°-sin 80°
=2sin 30°cos 10°+sin 60°-sin 80°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
7.cos 20°sin 50°-cos 70°sin 40°=___;cos 20°+cos 100°+
cos 140°=____.
解析 cos 20°sin 50°-cos 70°sin 40°
0
cos 20°+cos 100°+cos 140°
=2cos 60°cos 40°+cos(180°-40°)
=cos 40°-cos 40°=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
8.设直角三角形中两锐角为A和B,则cos Acos B的取值范围是________.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10.求下列各式的值:
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)sin 138°-cos 12°+sin 54°.
解 sin 138°-cos 12°+sin 54°=sin 42°-cos 12°+sin 54°
=sin 42°-sin 78°+sin 54°=-2cos 60°sin 18°+sin 54°
=sin 54°-sin 18°=2cos 36°sin 18°
基础巩固
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
√
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
15.已知函数f(x)=2sin(ωx+φ)(ω>0),若存在x0∈R,使得f(x0+2)-f(x0)
=4,则ω的最小值为____.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
解析 4=f(x0+2)-f(x0)=2sin[ω(x0+2)+φ]
-2sin(ωx0+φ)=4sin ωcos[ω(x0+1)+φ],
所以sin ωcos[ω(x0+1)+φ]=1,
而|sin ω||cos[ω(x0+1)+φ]|≤1,
故等号成立,当且仅当|sin ω|=1,|cos[ω(x0+1)+φ]|=1,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
16.求函数f(x)=cos2(x+θ)-2cos θcos xcos(x+θ)+cos2θ的最小正周期、值域、单调区间.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
=1+cos(x+2θ)cos x-cos(x+2θ)cos x-cos2x
所以f(x)的最小正周期T=π,值域为[0,1],
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
综合运用
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
