苏教版(2019)高中数学必修第二册 第10章_章末复习课_课件(共38张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 第10章_章末复习课_课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:27:28 | ||
图片预览







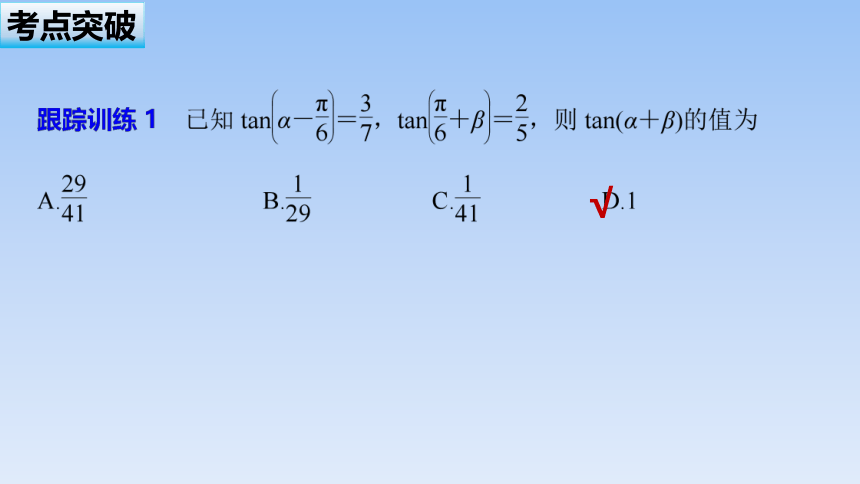

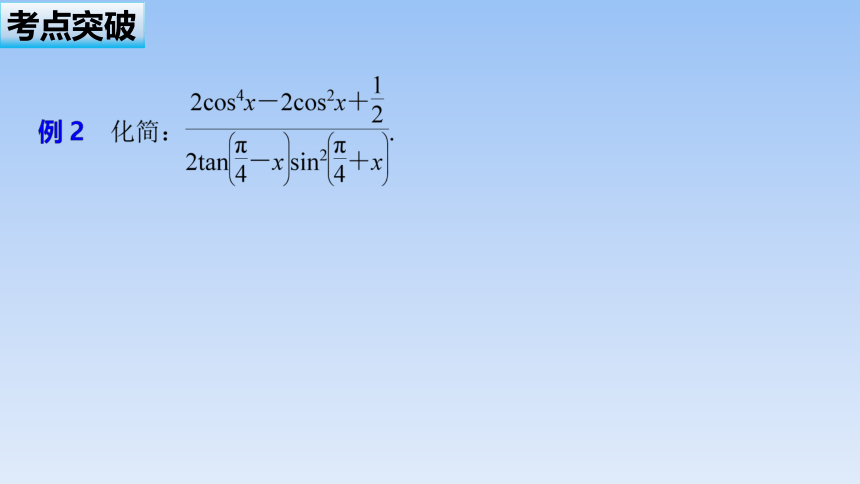
文档简介
(共38张PPT)
章末复习课
第十章 三角恒等变换
内
容
索
引
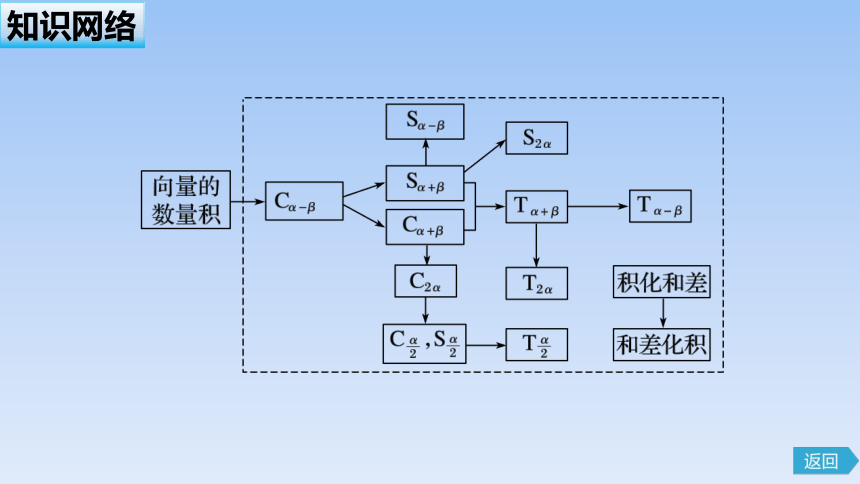
知识网络
考点突破
真题体验
1
知识网络
PART ONE
知识网络
2
考点突破
PART TWO
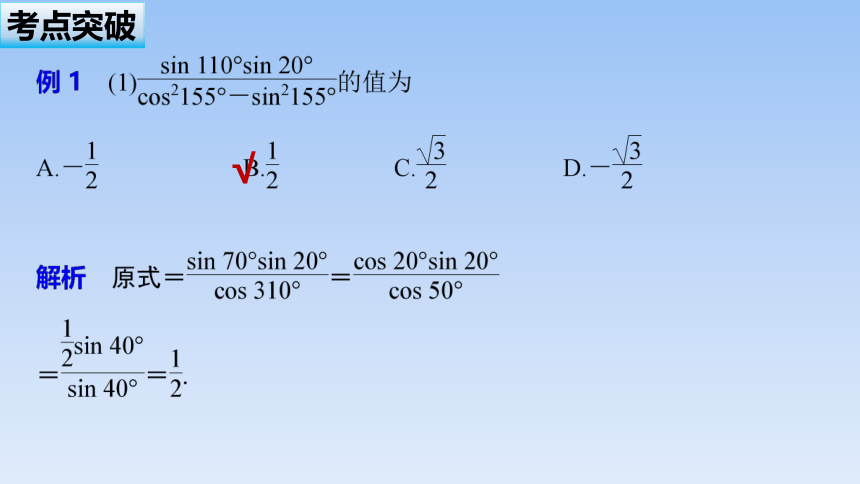
一、三角函数求值
1.掌握两角和与差的正弦、余弦、正切公式、二倍角公式、和差化积与积化和差公式的正用、逆用以及推论的应用.
2.掌握三角函数中公式的正用、逆用及变形用,重点提升逻辑推理和数学运算素养.
考点突破
√
考点突破
(2)设α为钝角,且3sin 2α=cos α,则sin α=___.
解析 因为α为钝角,所以sin α>0,cos α<0,
由3sin 2α=cos α,可得6sin αcos α=cos α,
考点突破
三角函数的求值问题通常包括三种类型,即给角求值,给值求值,给值求角.给角求值的关键是将要求角转化为特殊角的三角函数值;给值求值关键是找准要求角与已知角之间的联系,合理进行拆角、凑角;给值求角实质是给值求值,先求角的某一三角函数值,再确定角的范围,从而求出角.
反思感悟
√
考点突破
二、三角函数式的化简与证明
1.掌握两角和与差公式的正用、逆用以及倍角、半角公式的应用.
2.通过三角函数式的化简与证明,培养逻辑推理和数学运算素养.
考点突破
考点突破
考点突破
三角函数的化简常用的策略有:切化弦、异名化同名、降幂公式、1的代换等,化简的结果应做到项数尽可能少,次数尽可能低,函数名尽量统一.
三角函数的证明常用的方法有:从左向右(或从右向左),一般由繁向简;从两边向中间,左右归一法;作差证明,证明“左边-右边=0”;左右分子、分母交叉相乘,证明差值为0等.
反思感悟
考点突破
所以原等式成立.
考点突破
三、三角恒等变换与三角函数、向量的综合运用
1.三角函数与三角恒等变换综合问题,通常是通过三角恒等变换,如降幂公式,辅助角公式对三角函数式进行化简,最终化为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k的形式,再研究三角函数的性质.当问题以向量为载体时,一般是通过向量运算,将问题转化为三角函数形式,再运用三角恒等变换进行求解.
2.通过三角恒等变换与三角函数、向量的综合运用培养逻辑推理和数学运算素养.
考点突破
(1)求cos(α-β)的值;
解 因为向量a=(cos α,sin α),b=(cos β,sin β),
考点突破
所以sin α=sin[(α-β)+β]=sin(α-β)cos β+cos(α-β)sin β
考点突破
解决三角恒等变换与三角函数综合问题的关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等思想(切化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化、角的代换)的运用,还要注意一般的数学思想方法(如换元法等)的运用.
反思感悟
(1)化简f(x);
考点突破
考点突破
四、三角恒等变换的实际应用
1.建立关于三角函数的数学模型、利用三角恒等变换化简,运用三角函数的性质进行求解.
2.通过三角恒等变换实际应用,培养学生数学建模和数学运算的能力.
考点突破
例4 如图,将一块圆心角为120°,半径为20 cm的扇形铁片裁成一块矩形,有两种裁法,让矩形一边在扇形的半径OA上(如图①)或让矩形一边与弦AB平行(如图②),请问哪种裁法得到的矩形的面积最大?请求出这个最大值.
考点突破
解 对于题干图①,MN=20sin θ,ON=20cos θ,
所以S1=ON·MN=400sin θcos θ=200sin 2θ.
所以当sin 2θ=1,即θ=45°时,(S1)max=200 cm2.
对于题干图②,MQ=40sin(60°-α),
因为0°<α<60°,所以-60°<2α-60°<60°.
所以当cos(2α-60°)=1,即2α-60°=0°,
考点突破
所以用题干图②这种裁法得到的矩形的面积最大,
考点突破
建立关于三角函数的解析式,通过降幂公式、辅助角公式转化为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k的形式,利用三角函数的性质求值.
反思感悟
跟踪训练4 如图,ABCD是一块边长为100 m的正方形地皮,其中AST是半径为90 m的扇形小山,其余部分都是平地.一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在ST上,相邻两边CQ,CR正好落在正方形的边BC,CD上,求矩形停车场PQCR面积的最大值和最小值.
考点突破
则AM=90cos θ,MP=90sin θ.
所以PQ=MB=100-90cos θ,
PR=MR-MP=100-90sin θ.
所以S矩形PQCR=PQ·PR
=(100-90cos θ)(100-90sin θ)
=10 000-9 000(sin θ+cos θ)
+8 100sin θcos θ.
考点突破
考点突破
3
真题体验
PART THREE
解析 由3cos 2α-8cos α=5,
得3(2cos2α-1)-8cos α=5,即3cos2α-4cos α-4=0,
1.(2020·全国Ⅰ)已知α∈(0,π),且3cos 2α-8cos α=5,则sin α等于
√
1
2
3
4
5
又因为α∈(0,π),所以sin α>0,
真题体验
A.-2 B.-1 C.1 D.2
√
1
2
3
4
5
解得tan θ=2.
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
章末复习课
第十章 三角恒等变换
内
容
索
引
知识网络
考点突破
真题体验
1
知识网络
PART ONE
知识网络
2
考点突破
PART TWO
一、三角函数求值
1.掌握两角和与差的正弦、余弦、正切公式、二倍角公式、和差化积与积化和差公式的正用、逆用以及推论的应用.
2.掌握三角函数中公式的正用、逆用及变形用,重点提升逻辑推理和数学运算素养.
考点突破
√
考点突破
(2)设α为钝角,且3sin 2α=cos α,则sin α=___.
解析 因为α为钝角,所以sin α>0,cos α<0,
由3sin 2α=cos α,可得6sin αcos α=cos α,
考点突破
三角函数的求值问题通常包括三种类型,即给角求值,给值求值,给值求角.给角求值的关键是将要求角转化为特殊角的三角函数值;给值求值关键是找准要求角与已知角之间的联系,合理进行拆角、凑角;给值求角实质是给值求值,先求角的某一三角函数值,再确定角的范围,从而求出角.
反思感悟
√
考点突破
二、三角函数式的化简与证明
1.掌握两角和与差公式的正用、逆用以及倍角、半角公式的应用.
2.通过三角函数式的化简与证明,培养逻辑推理和数学运算素养.
考点突破
考点突破
考点突破
三角函数的化简常用的策略有:切化弦、异名化同名、降幂公式、1的代换等,化简的结果应做到项数尽可能少,次数尽可能低,函数名尽量统一.
三角函数的证明常用的方法有:从左向右(或从右向左),一般由繁向简;从两边向中间,左右归一法;作差证明,证明“左边-右边=0”;左右分子、分母交叉相乘,证明差值为0等.
反思感悟
考点突破
所以原等式成立.
考点突破
三、三角恒等变换与三角函数、向量的综合运用
1.三角函数与三角恒等变换综合问题,通常是通过三角恒等变换,如降幂公式,辅助角公式对三角函数式进行化简,最终化为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k的形式,再研究三角函数的性质.当问题以向量为载体时,一般是通过向量运算,将问题转化为三角函数形式,再运用三角恒等变换进行求解.
2.通过三角恒等变换与三角函数、向量的综合运用培养逻辑推理和数学运算素养.
考点突破
(1)求cos(α-β)的值;
解 因为向量a=(cos α,sin α),b=(cos β,sin β),
考点突破
所以sin α=sin[(α-β)+β]=sin(α-β)cos β+cos(α-β)sin β
考点突破
解决三角恒等变换与三角函数综合问题的关键在于熟练地运用基本的三角恒等变换思想方法,对其解析式变形、化简,尽量使其化为只有一个角为自变量的三角函数.解决与图象和性质有关的问题,在进行恒等变换时,既要注意三角恒等思想(切化弦、常值代换、降幂与升幂、收缩代换、和差与积的互化、角的代换)的运用,还要注意一般的数学思想方法(如换元法等)的运用.
反思感悟
(1)化简f(x);
考点突破
考点突破
四、三角恒等变换的实际应用
1.建立关于三角函数的数学模型、利用三角恒等变换化简,运用三角函数的性质进行求解.
2.通过三角恒等变换实际应用,培养学生数学建模和数学运算的能力.
考点突破
例4 如图,将一块圆心角为120°,半径为20 cm的扇形铁片裁成一块矩形,有两种裁法,让矩形一边在扇形的半径OA上(如图①)或让矩形一边与弦AB平行(如图②),请问哪种裁法得到的矩形的面积最大?请求出这个最大值.
考点突破
解 对于题干图①,MN=20sin θ,ON=20cos θ,
所以S1=ON·MN=400sin θcos θ=200sin 2θ.
所以当sin 2θ=1,即θ=45°时,(S1)max=200 cm2.
对于题干图②,MQ=40sin(60°-α),
因为0°<α<60°,所以-60°<2α-60°<60°.
所以当cos(2α-60°)=1,即2α-60°=0°,
考点突破
所以用题干图②这种裁法得到的矩形的面积最大,
考点突破
建立关于三角函数的解析式,通过降幂公式、辅助角公式转化为y=Asin(ωx+φ)+k或y=Acos(ωx+φ)+k的形式,利用三角函数的性质求值.
反思感悟
跟踪训练4 如图,ABCD是一块边长为100 m的正方形地皮,其中AST是半径为90 m的扇形小山,其余部分都是平地.一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在ST上,相邻两边CQ,CR正好落在正方形的边BC,CD上,求矩形停车场PQCR面积的最大值和最小值.
考点突破
则AM=90cos θ,MP=90sin θ.
所以PQ=MB=100-90cos θ,
PR=MR-MP=100-90sin θ.
所以S矩形PQCR=PQ·PR
=(100-90cos θ)(100-90sin θ)
=10 000-9 000(sin θ+cos θ)
+8 100sin θcos θ.
考点突破
考点突破
3
真题体验
PART THREE
解析 由3cos 2α-8cos α=5,
得3(2cos2α-1)-8cos α=5,即3cos2α-4cos α-4=0,
1.(2020·全国Ⅰ)已知α∈(0,π),且3cos 2α-8cos α=5,则sin α等于
√
1
2
3
4
5
又因为α∈(0,π),所以sin α>0,
真题体验
A.-2 B.-1 C.1 D.2
√
1
2
3
4
5
解得tan θ=2.
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
1
2
3
4
5
真题体验
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
