苏教版(2019)高中数学必修第一册《函数的表示方法》精品课件(共15张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册《函数的表示方法》精品课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 10:12:14 | ||
图片预览





文档简介
(共15张PPT)
苏教版同步教材精品课件
5.2函数的表示方法
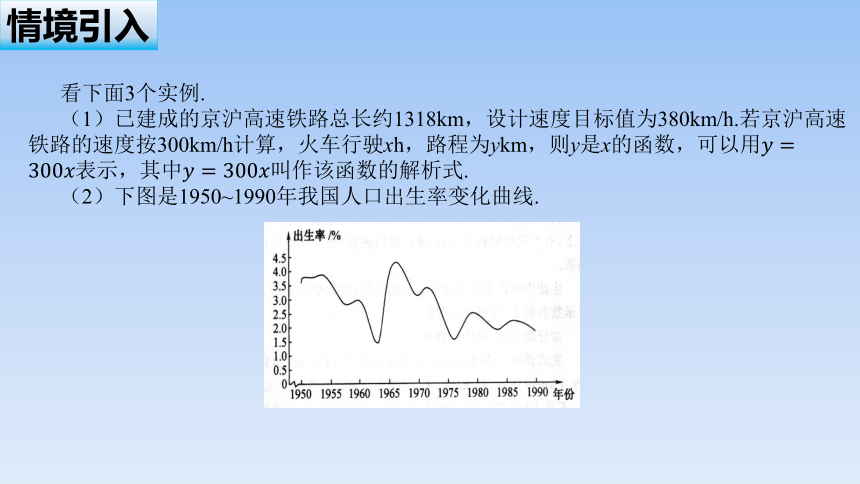
情境引入
看下面3个实例.
(1)已建成的京沪高速铁路总长约1318km,设计速度目标值为380km/h.若京沪高速铁路的速度按300km/h计算,火车行驶xh,路程为ykm,则y是x的函数,可以用表示,其中叫作该函数的解析式.
(2)下图是1950~1990年我国人口出生率变化曲线.
情境引入
(3)下表是大气中氰化物浓度与污染源距离的关系表.
问题:根据初中所学知识,请判断实例(1)(2)(3)分别是用什么方法表示函数的?
提示:解析法、图象法、列表法.
设计意图:通过具体例子,让学生体会用三种不同的方法表示函数,进一步理解函数的概念.
函数的表示方法:
(1)解析法:用等式来表示两个变量之间函数关系的方法如实例(1)(路程与速度).
(2)图象法:用图象表示两个变量之间函数关系的方法如实例(2)(人口出生率). (3)列表法:用列表来表示两个变量之间函数关系的方法.如实例(3)(氰化物浓度与污染源距离).
设计意图:通过总结函数的三种表示方法,提高学生的归纳概括能力.
探究新知
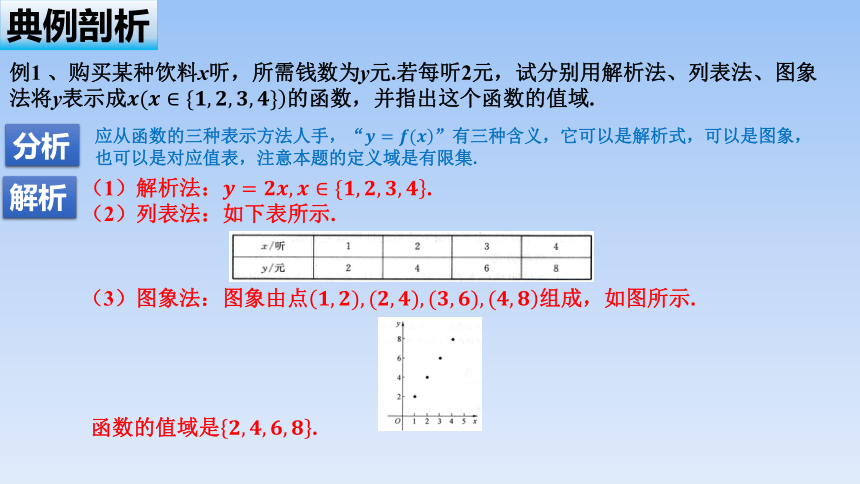
典例剖析
例1 、购买某种饮料x听,所需钱数为y元.若每听2元,试分别用解析法、列表法、图象法将y表示成的函数,并指出这个函数的值域.
解析
(1)解析法:.
(2)列表法:如下表所示.
分析
应从函数的三种表示方法人手,“”有三种含义,它可以是解析式,可以是图象,也可以是对应值表,注意本题的定义域是有限集.
(3)图象法:图象由点组成,如图所示.
函数的值域是.
思考
(1)这个函数的图象有什么特点?
这个函数的图象由一些离散的点组成,与以前学习过的一次函数、二次函数的图象是连续的曲线不同.通过本例,进一步让学生感受到,函数概念中的对应关系、定义域、值域是一个整体.函数不同于函数,前者的图象是一条(连续的)直线,后者的图象是4个离散的点.
(2)比较函数的三种表示方法,各自有哪些优点?
解析法有以下优点:一是简明、精确地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值;三是便于用解析式研究函数的性质中学阶段所研究的主要是能够用解析式表示的函数.
图象法的优点:直观形象地表示出函数的变化情况,有利于我们通过图象来研究函数的某些性质图象法在生产和生活中有许多应用,如企业生产图,股票指数走势图等.
列表法的优点:不必通过计算就可以知道自变量取某个值时,相应的函数值是多少.列表法在实际生产和生活中也有广泛应用,如成绩表、银行的利率表等.
典例剖析
(3)所有的函数都能用解析法表示吗?举出一个函数,并分别用三种表示方法表示.
提示:不是所有的函数都能用解析法表示,如心电图.
在讨论中,还可以问学生“函数图象可以是折线吗”,进一步引出例2.
典例剖析
典例剖析
例2、画出函数的图象,并求的值.
解析
因为
所以函数的图象为过原点且平分第一象限、第二象限的一条折线,如图所示.
其中,.
点评:
(1)函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等;(2)解析法:必须注明函数的定义域,否则使函数解析式有意义的自变量的取值范围是函数的定义域;(3)图象法:根据实际情境来决定是否连线;(4)列表法:选取的自变量要有代表性,应能反映函数的特征.
典例剖析
典例剖析
例3、某市出租汽车收费标准如下:在3km以内(含3km)路程按起步价9元收费,超过3km的路程按24元/km收费,试写出收费额(单位:元)关于路程(单位:km)的函数解析式.
解析
设路程为xkm时,收费额为y元,则由题意得:当时,;当时,按2.4元/km所收费用为,那么有.
于是,收费额关于路程的函数解析式为
即
设计意图:让学生尝试选择适当的表示方法来表示实际问题;学习分段函数及其表示.
例2例3中的函数具有共同特点:在定义域内不同部分上,有不同的解析表达式.像这样的函数,通常叫作分段函数.
生活中有许多需要分段表示的函数,请你举出几个分段函数的例子,并画出其图象.
如分期付款,邮件资费等.
典例剖析
变式训练
变式训练1:某市出租车资费规定如下:(1)3km以内(含3km)9元;(2)3km以上,每增加1km,资费增加2.4元(不足1km按1km计算).某线路总路程为6km,请根据题意写出资费关于路程的函数解析式,并画出函数的图象.
解析
设资费为y元,路程为x km.由题意知,自变量x的取值范围是.
y关于x的函数解析式为
根据解析式画出函数的图象如图所示.
变式训练
变式训练2:某市郊空调公共汽车的票价按下列规则制定:
(1)乘坐汽车5km以内,票价2元;
(2)5km以上,每增加5km,票价增加1元(不足5km按5km计算).
已知两个相邻的公共汽车站间相距约为1km,如果沿途(包括起点站和终点站)设20个汽车站,请根据题意,写出票价与路程之间的函数解析式,并画出函数的图象.
学生独立完成,集体核对答案.
课堂小结
1.理解函数的三种表示方法.
2.在具体的实际问题中能够选用恰当的表示方法来表示函数.
3.注意分段函数的表示方法及其图象的画法.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
作 业
教材第108页习题52第3,4,5题.
苏教版同步教材精品课件
5.2函数的表示方法
情境引入
看下面3个实例.
(1)已建成的京沪高速铁路总长约1318km,设计速度目标值为380km/h.若京沪高速铁路的速度按300km/h计算,火车行驶xh,路程为ykm,则y是x的函数,可以用表示,其中叫作该函数的解析式.
(2)下图是1950~1990年我国人口出生率变化曲线.
情境引入
(3)下表是大气中氰化物浓度与污染源距离的关系表.
问题:根据初中所学知识,请判断实例(1)(2)(3)分别是用什么方法表示函数的?
提示:解析法、图象法、列表法.
设计意图:通过具体例子,让学生体会用三种不同的方法表示函数,进一步理解函数的概念.
函数的表示方法:
(1)解析法:用等式来表示两个变量之间函数关系的方法如实例(1)(路程与速度).
(2)图象法:用图象表示两个变量之间函数关系的方法如实例(2)(人口出生率). (3)列表法:用列表来表示两个变量之间函数关系的方法.如实例(3)(氰化物浓度与污染源距离).
设计意图:通过总结函数的三种表示方法,提高学生的归纳概括能力.
探究新知
典例剖析
例1 、购买某种饮料x听,所需钱数为y元.若每听2元,试分别用解析法、列表法、图象法将y表示成的函数,并指出这个函数的值域.
解析
(1)解析法:.
(2)列表法:如下表所示.
分析
应从函数的三种表示方法人手,“”有三种含义,它可以是解析式,可以是图象,也可以是对应值表,注意本题的定义域是有限集.
(3)图象法:图象由点组成,如图所示.
函数的值域是.
思考
(1)这个函数的图象有什么特点?
这个函数的图象由一些离散的点组成,与以前学习过的一次函数、二次函数的图象是连续的曲线不同.通过本例,进一步让学生感受到,函数概念中的对应关系、定义域、值域是一个整体.函数不同于函数,前者的图象是一条(连续的)直线,后者的图象是4个离散的点.
(2)比较函数的三种表示方法,各自有哪些优点?
解析法有以下优点:一是简明、精确地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值;三是便于用解析式研究函数的性质中学阶段所研究的主要是能够用解析式表示的函数.
图象法的优点:直观形象地表示出函数的变化情况,有利于我们通过图象来研究函数的某些性质图象法在生产和生活中有许多应用,如企业生产图,股票指数走势图等.
列表法的优点:不必通过计算就可以知道自变量取某个值时,相应的函数值是多少.列表法在实际生产和生活中也有广泛应用,如成绩表、银行的利率表等.
典例剖析
(3)所有的函数都能用解析法表示吗?举出一个函数,并分别用三种表示方法表示.
提示:不是所有的函数都能用解析法表示,如心电图.
在讨论中,还可以问学生“函数图象可以是折线吗”,进一步引出例2.
典例剖析
典例剖析
例2、画出函数的图象,并求的值.
解析
因为
所以函数的图象为过原点且平分第一象限、第二象限的一条折线,如图所示.
其中,.
点评:
(1)函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等;(2)解析法:必须注明函数的定义域,否则使函数解析式有意义的自变量的取值范围是函数的定义域;(3)图象法:根据实际情境来决定是否连线;(4)列表法:选取的自变量要有代表性,应能反映函数的特征.
典例剖析
典例剖析
例3、某市出租汽车收费标准如下:在3km以内(含3km)路程按起步价9元收费,超过3km的路程按24元/km收费,试写出收费额(单位:元)关于路程(单位:km)的函数解析式.
解析
设路程为xkm时,收费额为y元,则由题意得:当时,;当时,按2.4元/km所收费用为,那么有.
于是,收费额关于路程的函数解析式为
即
设计意图:让学生尝试选择适当的表示方法来表示实际问题;学习分段函数及其表示.
例2例3中的函数具有共同特点:在定义域内不同部分上,有不同的解析表达式.像这样的函数,通常叫作分段函数.
生活中有许多需要分段表示的函数,请你举出几个分段函数的例子,并画出其图象.
如分期付款,邮件资费等.
典例剖析
变式训练
变式训练1:某市出租车资费规定如下:(1)3km以内(含3km)9元;(2)3km以上,每增加1km,资费增加2.4元(不足1km按1km计算).某线路总路程为6km,请根据题意写出资费关于路程的函数解析式,并画出函数的图象.
解析
设资费为y元,路程为x km.由题意知,自变量x的取值范围是.
y关于x的函数解析式为
根据解析式画出函数的图象如图所示.
变式训练
变式训练2:某市郊空调公共汽车的票价按下列规则制定:
(1)乘坐汽车5km以内,票价2元;
(2)5km以上,每增加5km,票价增加1元(不足5km按5km计算).
已知两个相邻的公共汽车站间相距约为1km,如果沿途(包括起点站和终点站)设20个汽车站,请根据题意,写出票价与路程之间的函数解析式,并画出函数的图象.
学生独立完成,集体核对答案.
课堂小结
1.理解函数的三种表示方法.
2.在具体的实际问题中能够选用恰当的表示方法来表示函数.
3.注意分段函数的表示方法及其图象的画法.
设计意图:通过总结,让学生进一步巩固本节所学内容,提高概括能力.
作 业
教材第108页习题52第3,4,5题.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
