苏教版(2019)高中数学必修第一册《函数的表示方法的应用》名师课件(共20张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册《函数的表示方法的应用》名师课件(共20张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:35:14 | ||
图片预览






文档简介
(共20张PPT)
复习引入
苏教版同步教材名师课件
函数的表示方法的应用
学习目标
学 习 目 标 核心素养
了解函数的三种表示法,掌握函数解析式的求法 数学抽象
掌握分段函数的简单应用 逻辑推理
理解函数图像的作用,掌握函数图象的三种变换 直观想象
课程目标
1、明确函数的三种表示方法;
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养
1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型.
学习目标
新知讲解
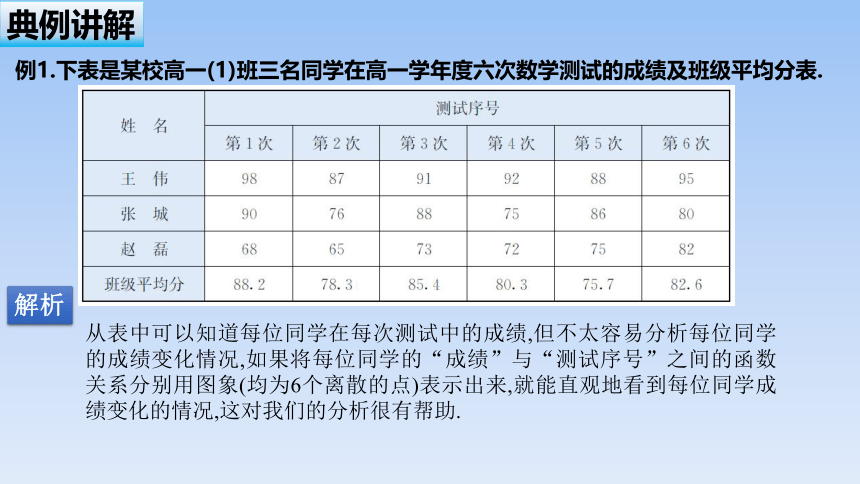
表示法 优 点 缺 点
解析法 一是简明、全面概括了变量间的关系;二是利用解析式可求任一函数值 不够形象、直观,而且并不是所有函数都有解析式
列表法 不需计算,可以直接看出与自变量对应的函数值 仅能表示自变量取较少的有限值时的对应关系
图像法 能形象、直观地表示函数的变化情况 只能近似求出自变量的值所对应的函数值,而且有时误差较大
典例讲解
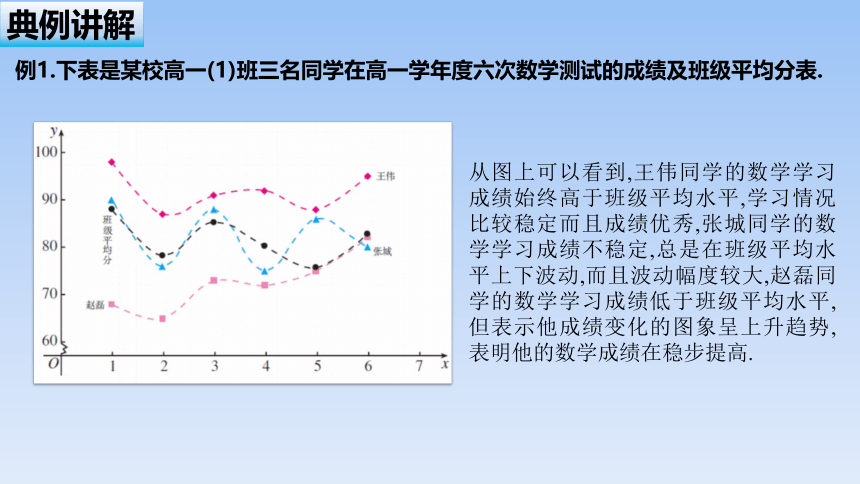
例1.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
解析
从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况,如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
典例讲解
例1.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
从图上可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀,张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大,赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
典例讲解
例2.经市场调查,某商品在近100天内,其销售量和价格均是时间的函数,且销售量近似地满足关系在前40天内价格为在后60天内价格为求这种商品的日销售额的最大值(近似到1元).
日销售额=销售量×价格,而价格根据时间的不同,表达式也不一样,很明显,这是一道关于分段函数的题目.
思路分析
前40天内日销售额为:
,
.
后60天内日销售额为:
,
,
解析
典例讲解
例2.经市场调查,某商品在近100天内,其销售量和价格均是时间的函数,且销售量近似地满足关系在前40天内价格为在后60天内价格为求这种商品的日销售额的最大值(近似到1元).
解析
由上式可知:对于,有当或11时,;对于,有当时, 714.综上所述得:当或11时,.
答:第10天或11天日销售额最大值为809元.
方法归纳
解函数应用题的一般步骤:
(1)首先在阅读材料、理解题意的基础上,把实际问题抽象为函数问题;
(2)利用函数知识建立相应的函数模型;
(3)再利用函数知识对函数模型进行分析、研究,得出数学结论;
(4)最后把数学结论(结果)应用到实际问题中.
典例讲解
如图(2)所示,分点在线段上三种情况,利用面积公式得出每种情况的解析式,最后合在一起即可.
思路分析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
典例讲解
解析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
过点分别作,垂足分别是
因为四边形是等腰梯形,底角为,cm,
所以,又,所以.
(1)当点在上,即时,;
(2)当点在上,即时,;
(3)当点在上,即时,
.
典例讲解
解析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
综合(1)(2)(3),得所求函数的解析式为
图象如右图所示:
变式训练
2.如图所示,在边长为4的正方形上有一点,沿着折线由点起点向点终点移动.设点移动的路程为,的面积为.
解析
(1)求的面积与移动的路程的函数关系式;
(2)画出函数的图象,并根据图象求的最大值.
函数的定义域为.
;
;
所以函数解析式为
(2)图象如图所示:
当堂练习
1.下列说法正确的个数是( )
①解析法能简明、全面地概述变量间的关系,是表示函数的最好方法;
②函数与的图象相同;
③直线与函数的图象可能有0个或1个交点.
A.0 B.1 C.2 D.3
B
函数的三种表示法各有优点、缺点,不存在最好的表示法一说,故①不正确; ②中函数的定义域不同,显然是两个函数,从而图象不同;③正确,当在定义域内时有一个交点,否则无交点.
当堂练习
D
2.的图象如图所示,其中时是一段顶点在坐标原点的抛物线,则 的解析式是( )
A.
B.
C.
D.
观察图象可知,当时,排除选项A.C;当时,排除选项B
当堂练习
3 .汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图象可能是( )
A
由这一过程中汽车的速度变化可知,速度由小变大→保持匀速→由大变小.速度由小变大时,路程曲线上升得越来越快,曲线显得陡峭;匀速行驶中路程曲线上升速度不变;速度由大变小时,路程曲线上升得越来越慢,曲线显得平缓.
当堂练习
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米元收费;用水超过10立方米的,超过部分按每立方米元收费·某职工某月缴水费元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米 C.18立方米 D.26立方米
A
该单位职工每月应缴水费y与实际用水量 满足的关系式为
由,可知.令,解得.
归纳小结
重点 函数表示法的应用
难点 函数表示法间的相互转化
易错 在写分段函数的解析式,及画分段函数的图象时,一定不要忽略函数的定义域
作 业
课本P109:10
复习引入
苏教版同步教材名师课件
函数的表示方法的应用
学习目标
学 习 目 标 核心素养
了解函数的三种表示法,掌握函数解析式的求法 数学抽象
掌握分段函数的简单应用 逻辑推理
理解函数图像的作用,掌握函数图象的三种变换 直观想象
课程目标
1、明确函数的三种表示方法;
2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;
3、通过具体实例,了解简单的分段函数,并能简单应用.
数学学科素养
1.数学抽象:函数解析法及能由条件求出解析式;
2.逻辑推理:由条件求函数解析式;
3.数学运算:由函数解析式求值及函数解析式的计算;
4.数据分析:利用图像表示函数;
5.数学建模:由实际问题构建合理的函数模型.
学习目标
新知讲解
表示法 优 点 缺 点
解析法 一是简明、全面概括了变量间的关系;二是利用解析式可求任一函数值 不够形象、直观,而且并不是所有函数都有解析式
列表法 不需计算,可以直接看出与自变量对应的函数值 仅能表示自变量取较少的有限值时的对应关系
图像法 能形象、直观地表示函数的变化情况 只能近似求出自变量的值所对应的函数值,而且有时误差较大
典例讲解
例1.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
解析
从表中可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况,如果将每位同学的“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
典例讲解
例1.下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
从图上可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀,张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大,赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
典例讲解
例2.经市场调查,某商品在近100天内,其销售量和价格均是时间的函数,且销售量近似地满足关系在前40天内价格为在后60天内价格为求这种商品的日销售额的最大值(近似到1元).
日销售额=销售量×价格,而价格根据时间的不同,表达式也不一样,很明显,这是一道关于分段函数的题目.
思路分析
前40天内日销售额为:
,
.
后60天内日销售额为:
,
,
解析
典例讲解
例2.经市场调查,某商品在近100天内,其销售量和价格均是时间的函数,且销售量近似地满足关系在前40天内价格为在后60天内价格为求这种商品的日销售额的最大值(近似到1元).
解析
由上式可知:对于,有当或11时,;对于,有当时, 714.综上所述得:当或11时,.
答:第10天或11天日销售额最大值为809元.
方法归纳
解函数应用题的一般步骤:
(1)首先在阅读材料、理解题意的基础上,把实际问题抽象为函数问题;
(2)利用函数知识建立相应的函数模型;
(3)再利用函数知识对函数模型进行分析、研究,得出数学结论;
(4)最后把数学结论(结果)应用到实际问题中.
典例讲解
如图(2)所示,分点在线段上三种情况,利用面积公式得出每种情况的解析式,最后合在一起即可.
思路分析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
典例讲解
解析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
过点分别作,垂足分别是
因为四边形是等腰梯形,底角为,cm,
所以,又,所以.
(1)当点在上,即时,;
(2)当点在上,即时,;
(3)当点在上,即时,
.
典例讲解
解析
例3.如图(1)所示,已知底角为的等腰梯形,底边长为7cm,腰长为cm,当垂直于底边(垂足为F)的直线从左至右移动(与梯形ABCD有公共点)时,直线把梯形分成两部分,令,试写出左边部分的面积关于的函数解析式,并画出大致图象.
综合(1)(2)(3),得所求函数的解析式为
图象如右图所示:
变式训练
2.如图所示,在边长为4的正方形上有一点,沿着折线由点起点向点终点移动.设点移动的路程为,的面积为.
解析
(1)求的面积与移动的路程的函数关系式;
(2)画出函数的图象,并根据图象求的最大值.
函数的定义域为.
;
;
所以函数解析式为
(2)图象如图所示:
当堂练习
1.下列说法正确的个数是( )
①解析法能简明、全面地概述变量间的关系,是表示函数的最好方法;
②函数与的图象相同;
③直线与函数的图象可能有0个或1个交点.
A.0 B.1 C.2 D.3
B
函数的三种表示法各有优点、缺点,不存在最好的表示法一说,故①不正确; ②中函数的定义域不同,显然是两个函数,从而图象不同;③正确,当在定义域内时有一个交点,否则无交点.
当堂练习
D
2.的图象如图所示,其中时是一段顶点在坐标原点的抛物线,则 的解析式是( )
A.
B.
C.
D.
观察图象可知,当时,排除选项A.C;当时,排除选项B
当堂练习
3 .汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车,若把这一过程中汽车的行驶路程看作时间的函数,其图象可能是( )
A
由这一过程中汽车的速度变化可知,速度由小变大→保持匀速→由大变小.速度由小变大时,路程曲线上升得越来越快,曲线显得陡峭;匀速行驶中路程曲线上升速度不变;速度由大变小时,路程曲线上升得越来越慢,曲线显得平缓.
当堂练习
4. 某单位为鼓励职工节约用水,作出了如下规定:每位职工每月用水不超过10立方米的,按每立方米元收费;用水超过10立方米的,超过部分按每立方米元收费·某职工某月缴水费元,则该职工这个月实际用水为( )
A.13立方米 B.14立方米 C.18立方米 D.26立方米
A
该单位职工每月应缴水费y与实际用水量 满足的关系式为
由,可知.令,解得.
归纳小结
重点 函数表示法的应用
难点 函数表示法间的相互转化
易错 在写分段函数的解析式,及画分段函数的图象时,一定不要忽略函数的定义域
作 业
课本P109:10
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
