苏教版(2019)高中数学必修第一册 5.2 函数的表示方法【导学案解析版】
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 5.2 函数的表示方法【导学案解析版】 |

|
|
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:36:29 | ||
图片预览




文档简介
第5章 函数概念与性质
第02讲 函数的表示方法
课程标准 重难点
1.会根据不同的需要选择恰当的方法(如图象发、列表法、解析法)表示函数;2.理解函数图象的作用;3.会求函数的解析式. 1.函数的图象及其应用2.函数的解析式求法
一、函数的表示方法
1.任何一个函数都可以用解析法、列表法、图表法三种形式表示吗?
2.三种表示函数方法的优缺点:
二、分段函数
1.一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
2.分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
3.作分段函数图象时,应分别作出每一段的图象.
4.分段函数是一个函数还是几个函数?
一、1. 不一定.并不是所有的函数都可以用解析式表示,不仅如此,图象法也不适用于所有函数,
如D(x)=列表法虽在理论上适用于所有函数,但对于自变量有无数个取值的情况,列表法只能表示函数的一个概况或片段.
二、1.对应关系 2.并集 空集 4. 分段函数是一个函数,而不是几个函数.
考法01 函数的三种表示方法
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在用三种方法表示函数时要注意:①解析法必须注明函数的定义域;②列表法中选取的自变量要有代表性,应能反映定义域的特征;③图象法中要注意是否连线.
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
【跟踪训练】已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
(1)f(g(1))=________;(2)若g(f(x))=2,则x=________.
(2)由表知g(2)=2,又因g(f(x))=2,得f(x)=2,再由表知x=1.
考法02 函数的图象及应用
描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象.
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心圈.
注意:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
作出下列函数图象并指出其值域:
(1)y=1-x(x∈Z且|x|≤2);(2)y=2x2-4x-3(0≤x<3).
【跟踪训练】画出下列函数的图象:
(1)y=x+1(x≤0);(2)y=x2-2x(x>1,或x<-1).
考法03 函数的解析式
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
求下列函数的解析式:
(1)已知函数f(+1)=x+2,求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1)-f(x)=2x,求f(x).
(3)已知f(x)+2f(-x)=x2+2x,求f(x).
【跟踪训练】
变式1. (变条件)在例3(2)中,把条件换为“函数f(x)是一次函数,且f(f(x))=4x+8”,求f(x).
变式2. (变条件)在例3(3)中把条件换为“2f+f(x)=x(x≠0)”,求f(x)。
题组A 基础过关练
1.图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
2.如图,设有圆O和定点C,当从开始在平面上绕O匀速旋转(旋转角度不超过)时,它扫过圆内阴影部分面积S是时间t的函数,它的图像大致是如下哪一种( )
A.B.
C. D.
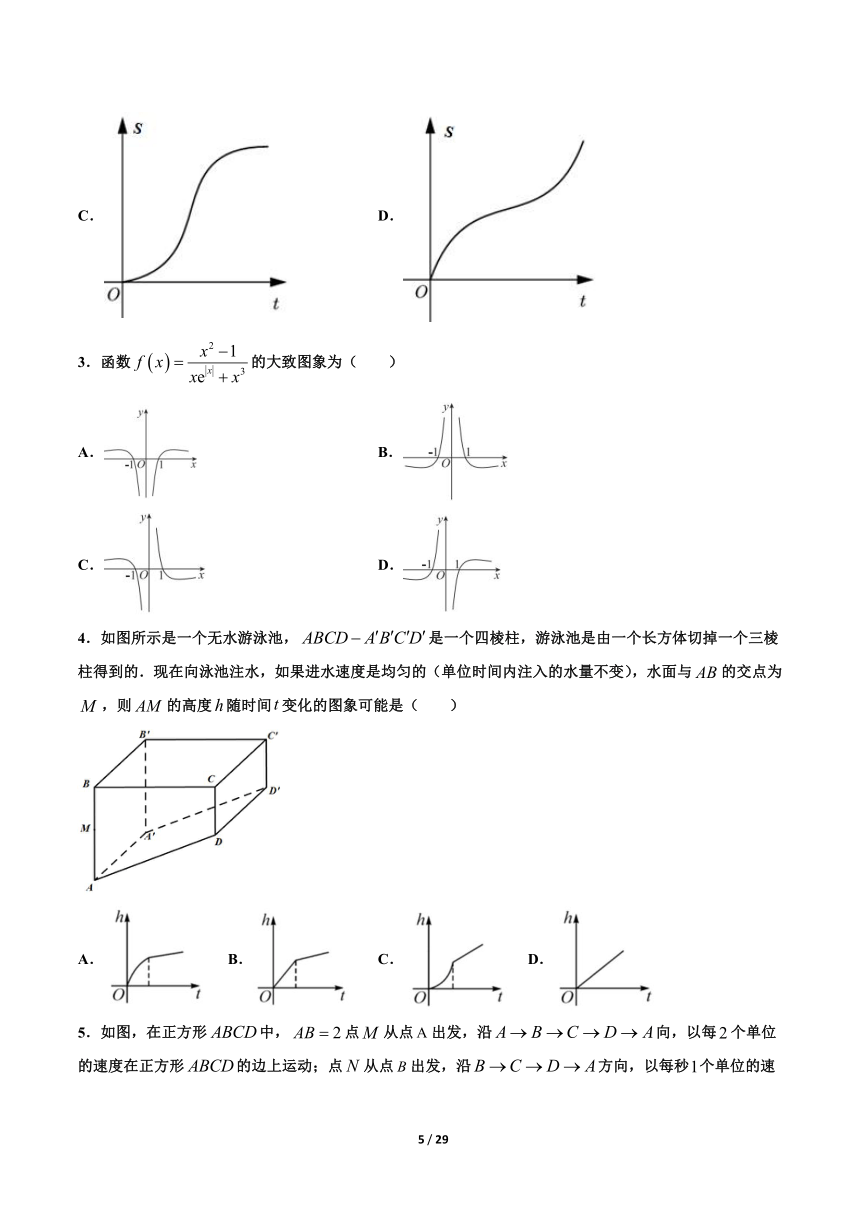
3.函数的大致图象为( )
A. B.
C. D.
4.如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
5.如图,在正方形中,点从点出发,沿向,以每个单位的速度在正方形的边上运动;点从点出发,沿方向,以每秒个单位的速度在正方形的边上运动.点与点同时出发,运动时间为(单位:秒),的面积为(规定共线时其面积为零,则点第一次到达点时,的图象为( )
A. B.
C. D.
6.函数的部分图象大致为( )
A. B.
C. D.
7.已知函数,若,则的取值集合是( )
A. B.
C. D.
8.设,则的值为( )
A.16 B.18 C.21 D.24
题组B 能力提升练
1.若函数,值域为,则( )
A. B.
C. D.
2.在某种固体金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示,在实验过程中金属材料没有熔化.则下列结论正确的是( )
A.以后温度基本保持不变
B.前温度增加的速度越来越快
C.前温度增加的速度越来越慢
D.实验表明这种金属材料是耐高温的好材料
3.假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者,现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以表示,被捕食者的数量以表示.下图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法不正确的是( )
A.若在、时刻满足:,则
B.如果数量是先上升后下降的,那么的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数与捕食者数总和达到最大值时,捕食者的数量也会达到最大值
4.已知,,则的解析式为________.
5.函数,则__________(注明定义域)
6.已知一次函数满足,则=________.
7.已知函数,,.
(1)在图中画出函数,的图象;
(2)定义:,用表示,中的较小者,记为,请分别用图象法和解析式法表示函数.(注:图象法请在图中表示,本题中的单位长度请自己定义且标明)
8.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的表达式;
题组C 培优拔尖练
1.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
2.设函数,则满足的的取值范围是( )
A. B. C. D.
3.已知,则函数的值域为________.
4.若,则________.
5.已知函数,函数,其中
(1)若恒成立,求实数t的取值范围;
(2)若,
①求使得成立的x的取值范围;
②求在区间上的最大值.
6.已知函数,.
(1)求的表达式;
(2)求方程 解.
第5章 函数概念与性质
第02讲 函数的表示方法答案
课程标准 重难点
1.会根据不同的需要选择恰当的方法(如图象发、列表法、解析法)表示函数;2.理解函数图象的作用;3.会求函数的解析式. 1.函数的图象及其应用2.函数的解析式求法
一、函数的表示方法
1.任何一个函数都可以用解析法、列表法、图表法三种形式表示吗?
2.三种表示函数方法的优缺点:
二、分段函数
1.一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
2.分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
3.作分段函数图象时,应分别作出每一段的图象.
4.分段函数是一个函数还是几个函数?
一、1. 不一定.并不是所有的函数都可以用解析式表示,不仅如此,图象法也不适用于所有函数,
如D(x)=列表法虽在理论上适用于所有函数,但对于自变量有无数个取值的情况,列表法只能表示函数的一个概况或片段.
二、1.对应关系 2.并集 空集 4. 分段函数是一个函数,而不是几个函数.
考法01 函数的三种表示方法
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在用三种方法表示函数时要注意:①解析法必须注明函数的定义域;②列表法中选取的自变量要有代表性,应能反映定义域的特征;③图象法中要注意是否连线.
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
【解析】用图象法表示函数y=f(x),如图所示.
用列表法表示函数y=f(x),如表所示.
x 1 2 3 4
y -2 -3 -4 -5
【跟踪训练】已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
(1)f(g(1))=________;(2)若g(f(x))=2,则x=________.
【答案】(1)1 (2)1
【解析】(1)由表知g(1)=3,∴f(g(1))=f(3)=1.
(2)由表知g(2)=2,又因g(f(x))=2,得f(x)=2,再由表知x=1.
考法02 函数的图象及应用
描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象.
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心圈.
注意:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
作出下列函数图象并指出其值域:
(1)y=1-x(x∈Z且|x|≤2);(2)y=2x2-4x-3(0≤x<3).
【解析】 (1)∵x∈Z且|x|≤2,∴x∈{-2,-1,0,1,2}.所以图象为一直线上的孤立点,如图所示.由图可知函数的值域为{3,2,1,0, -1}
(2)∵y=2(x-1)2-5,∴当x=0时,y=-3;
当x=3时,y=3;当x=1时,y=-5.所画函数图象如图所示.
由图可知函数的值域为[-5,3)
【跟踪训练】画出下列函数的图象:
(1)y=x+1(x≤0);(2)y=x2-2x(x>1,或x<-1).
【解析】 (1)y=x+1(x≤0)表示一条射线,图象如图①.
(2)y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-2x去掉-1≤x≤1之间的部分后剩余曲线.如图②.
考法03 函数的解析式
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
求下列函数的解析式:
(1)已知函数f(+1)=x+2,求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1)-f(x)=2x,求f(x).
(3)已知f(x)+2f(-x)=x2+2x,求f(x).
【解析】(1)方法一:(换元法)设t=+1,则x=(t-1)2(t≥1).
∴f(t)=(t-1)2+2(t-1)=t2-2t+1+2t-2=t2-1,∴f(x)=x2-1(x≥1).
方法二:(配凑法)∵x+2=()2+2+1-1=(+1)2-1,
∴f(+1)=(+1)2-1(+1≥1),∴f(x)=x2-1(x≥1).
(2)设f(x)=ax2+bx+c(a≠0).∵f(0)=1,∴c=1.
又∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
整理,得2ax+(a+b)=2x.
由恒等式的性质,知上式中对应项的系数相等,
∴解得∴f(x)=x2-x+1.
(3)∵f(x)+2f(-x)=x2+2x,①
∴将x换成-x,得f(-x)+2f(x)=x2-2x.②
∴由①②得3f(x)=x2-6x,∴f(x)=x2-2x.
【跟踪训练】
变式1. (变条件)在例3(2)中,把条件换为“函数f(x)是一次函数,且f(f(x))=4x+8”,求f(x).
【解析】设f(x)=ax+b(a≠0),则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又f(f(x))=4x+8,∴a2x+ab+b=4x+8,
即,解得或∴f(x)=2x+或f(x)=-2x-8.
变式2. (变条件)在例3(3)中把条件换为“2f+f(x)=x(x≠0)”,求f(x)。
【解析】由f(x)+2f=x,令x=,得f+2f(x)=,
于是得关于f(x)与f的方程组解得f(x)=- (x≠0)。
题组A 基础过关练
1.图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
【答案】A
【解析】水壶的结构:低端与上端细、中间粗,
所以在注水恒定的情况下:
开始水的高度增加的快,中间增加的慢,最后水上升的速度又变快,
由图可知选项A符合,故选:A
2.如图,设有圆O和定点C,当从开始在平面上绕O匀速旋转(旋转角度不超过)时,它扫过圆内阴影部分面积S是时间t的函数,它的图像大致是如下哪一种( )
A.B.
C. D.
【答案】C
【解析】当直线从初始位置转到经过点的过程中阴影部分面积增加的越来越快,图像越来越“陡峭”;
从过点的位置转至结束时阴影部分面积增加的越来越慢,图像越来越“平缓”,
故选:C.
3.函数的大致图象为( )
A. B.
C. D.
【答案】D
【解析】因为,所以定义域为,关于原点对称,
因为,所以为奇函数,排除A、B,
又因为当时,,排除C.故选:D.
4.如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
【答案】A
【解析】由题意可知,当往游泳池内注水时,游泳池内的水呈“直棱柱”状,且直棱柱的高不变,
刚开始水面面积逐渐增大,水的高度增长得越来越慢,
当水面经过点后,水面的面积为定值,水的高度匀速增长,
故符合条件的函数图象为A选项中的图象.故选:A.
5.如图,在正方形中,点从点出发,沿向,以每个单位的速度在正方形的边上运动;点从点出发,沿方向,以每秒个单位的速度在正方形的边上运动.点与点同时出发,运动时间为(单位:秒),的面积为(规定共线时其面积为零,则点第一次到达点时,的图象为( )
A. B.
C. D.
【答案】A
【解析】根据题意,当,的面积为;
当,的面积为;
当,的面积为;
当,的面积为;
所以
所以根据分段函数的解析式即可得在区间上的函数图像为选项A.故选:A.
6.函数的部分图象大致为( )
A. B.
C. D.
【答案】A
【解析】因为,所以,
所以,且的定义域为关于原点对称,
所以为奇函数,排除B、D;
当时,,且,,所以,排除C,故选:A.
7.已知函数,若,则的取值集合是( )
A. B.
C. D.
【答案】A
【解析】若,可得,解得,(舍去);
若,可得=5,可得,与相矛盾,故舍去,
综上可得:.故选:A.
8.设,则的值为( )
A.16 B.18 C.21 D.24
【答案】B
【解析】因为,所以.
题组B 能力提升练
1.若函数,值域为,则( )
A. B.
C. D.
【答案】ACD
【解析】对于A,当,,则恒成立,
所以在上为单调递增函数,因为,故,故选项A正确;
且,故当时,值域为;
对于C,当时,则恒成立,
所以在上单调递减,所以,故,
又的值域为,所以,故,故选项C正确;
对于B,由选项C可知,,故,
所以,,
令,(),
所以,
当时,,则单调递增,
当时,,
此时,故选项B错误;
对于D,设,则,
令,则在恒成立,在上单调递增,
因此时,,,∴是减函数,
又,∴,即,
所以,则D正确.
故选:ACD.
2.在某种固体金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示,在实验过程中金属材料没有熔化.则下列结论正确的是( )
A.以后温度基本保持不变
B.前温度增加的速度越来越快
C.前温度增加的速度越来越慢
D.实验表明这种金属材料是耐高温的好材料
【答案】ACD
【解析】由图象可知前中温度增加,但是增加速度越来越慢,所以C对,B错.
以后温度图象是一条水平线,所以温度保持不变,A对,D对.故选:ACD.
3.假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者,现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以表示,被捕食者的数量以表示.下图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法不正确的是( )
A.若在、时刻满足:,则
B.如果数量是先上升后下降的,那么的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数与捕食者数总和达到最大值时,捕食者的数量也会达到最大值
【答案】ABD
【解析】由图可知,曲线中纵坐标相等时横坐标未必相等,故A不正确;
在曲线上半段中观察到是先上升后下降,而是不断变小的,故B不正确;
捕食者数量最大时是在图象最右端,最小值是在图象最左端,此时都不是被捕食者的数量的最值处,
同样当被捕食者的数量最大即图象最上端和最小即图象最下端时,也不是捕食者数量取最值的时候,
所以被捕食者数量和捕食者数量不会同时达到最大和最小值,故C正确;
当捕食者数量最大时在图象最右端,,,
此时二者总和,由图象可知存在点,,
,所以并不是被捕食者数量与捕食者数量总和达到最大值时,
被捕食者数量也会达到最大值,故D错误,故选:ABD.
4.已知,,则的解析式为________.
【答案】
【解析】由题知,,①;又,②;
由①②得,,
则,
故答案为:
5.函数,则__________(注明定义域)
【答案】
【解析】令,则,,
所以,,
所以.
故答案为:.
6.已知一次函数满足,则=________.
【答案】
【解析】设,则由,
得,即,故解得,
所以.
故答案为:.
7.已知函数,,.
(1)在图中画出函数,的图象;
(2)定义:,用表示,中的较小者,记为,请分别用图象法和解析式法表示函数.(注:图象法请在图中表示,本题中的单位长度请自己定义且标明)
【解析】(1),的图象如下图所示:
(2)当时,,则;
当时,,则;
当时,,则;
综上所述:.
图象如下图所示:
8.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的表达式;
【解析】(1)由于流量R与管道半径r的四次方成正比,所以函数解析式为.
(2)由r=3 cm,R=400 cm3/s,得k·34=400,∴,∴流量R的表达式为.
题组C 培优拔尖练
1.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
【答案】BD
【解析】由题意知函数的定义域为,故A错误;
当时,的取值范围是,当时,的取值范围是,因此的值域为,故B正确;
当时,,故C错误;
当时,,解得(舍去),当时,,解得
或(舍去),故D正确;
当时,,解得,当时,,解得,因此的解集为;故E错误.故选:BD.
2.设函数,则满足的的取值范围是( )
A. B. C. D.
【答案】D
【解析】因为,
所以,
,
(1)当时,,
若要,只需要 ,
即,
所以;
(2)当时,,
若要,
只需要,即,
所以.
综上所述,实数的取值范围是.
故选:D.
3.已知,则函数的值域为________.
【答案】
【解析】由题:,
,,所以的值域,
令,
函数的值域即,的值域,
,
当时,,当时,,
所以其值域为.
综上所述:函数的值域为.
故答案为:
4.若,则________.
【答案】
【解析】令,则,.
原式可变为①,
用代替t,则有②,
由①②消去得,
.故答案为:
5.已知函数,函数,其中
(1)若恒成立,求实数t的取值范围;
(2)若,
①求使得成立的x的取值范围;
②求在区间上的最大值.
【解析】(1)因为恒成立,所以恒成立,
所以恒成立,所以,解得,
所以;
(2)①当时,,所以,解得;
当时,,所以,
因为,所以,
所以无解,
综上所述:的取值范围是;
②由①可知:,
当时,,所以,所以;
当时,的对称轴为,所以,
且,所以,
令,所以,所以,
综上可知:.
6.已知函数,.
(1)求的表达式;
(2)求方程 解.
【解析】(1)当时,则,
,;
当时,则,
, ,;
当时,则,
, ,;
.
(2)当时,则,,
,,
,
,;
当时,则,,
,,
,无解;
当时,则,,
,,
,
,,
的解为,.
目标导航
知识精讲
能力拓展
例1
例2
例3
分层提分
目标导航
知识精讲
能力拓展
例1
例2
例3
分层提分
10 / 29
第02讲 函数的表示方法
课程标准 重难点
1.会根据不同的需要选择恰当的方法(如图象发、列表法、解析法)表示函数;2.理解函数图象的作用;3.会求函数的解析式. 1.函数的图象及其应用2.函数的解析式求法
一、函数的表示方法
1.任何一个函数都可以用解析法、列表法、图表法三种形式表示吗?
2.三种表示函数方法的优缺点:
二、分段函数
1.一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
2.分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
3.作分段函数图象时,应分别作出每一段的图象.
4.分段函数是一个函数还是几个函数?
一、1. 不一定.并不是所有的函数都可以用解析式表示,不仅如此,图象法也不适用于所有函数,
如D(x)=列表法虽在理论上适用于所有函数,但对于自变量有无数个取值的情况,列表法只能表示函数的一个概况或片段.
二、1.对应关系 2.并集 空集 4. 分段函数是一个函数,而不是几个函数.
考法01 函数的三种表示方法
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在用三种方法表示函数时要注意:①解析法必须注明函数的定义域;②列表法中选取的自变量要有代表性,应能反映定义域的特征;③图象法中要注意是否连线.
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
【跟踪训练】已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
(1)f(g(1))=________;(2)若g(f(x))=2,则x=________.
(2)由表知g(2)=2,又因g(f(x))=2,得f(x)=2,再由表知x=1.
考法02 函数的图象及应用
描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象.
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心圈.
注意:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
作出下列函数图象并指出其值域:
(1)y=1-x(x∈Z且|x|≤2);(2)y=2x2-4x-3(0≤x<3).
【跟踪训练】画出下列函数的图象:
(1)y=x+1(x≤0);(2)y=x2-2x(x>1,或x<-1).
考法03 函数的解析式
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
求下列函数的解析式:
(1)已知函数f(+1)=x+2,求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1)-f(x)=2x,求f(x).
(3)已知f(x)+2f(-x)=x2+2x,求f(x).
【跟踪训练】
变式1. (变条件)在例3(2)中,把条件换为“函数f(x)是一次函数,且f(f(x))=4x+8”,求f(x).
变式2. (变条件)在例3(3)中把条件换为“2f+f(x)=x(x≠0)”,求f(x)。
题组A 基础过关练
1.图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
2.如图,设有圆O和定点C,当从开始在平面上绕O匀速旋转(旋转角度不超过)时,它扫过圆内阴影部分面积S是时间t的函数,它的图像大致是如下哪一种( )
A.B.
C. D.
3.函数的大致图象为( )
A. B.
C. D.
4.如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
5.如图,在正方形中,点从点出发,沿向,以每个单位的速度在正方形的边上运动;点从点出发,沿方向,以每秒个单位的速度在正方形的边上运动.点与点同时出发,运动时间为(单位:秒),的面积为(规定共线时其面积为零,则点第一次到达点时,的图象为( )
A. B.
C. D.
6.函数的部分图象大致为( )
A. B.
C. D.
7.已知函数,若,则的取值集合是( )
A. B.
C. D.
8.设,则的值为( )
A.16 B.18 C.21 D.24
题组B 能力提升练
1.若函数,值域为,则( )
A. B.
C. D.
2.在某种固体金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示,在实验过程中金属材料没有熔化.则下列结论正确的是( )
A.以后温度基本保持不变
B.前温度增加的速度越来越快
C.前温度增加的速度越来越慢
D.实验表明这种金属材料是耐高温的好材料
3.假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者,现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以表示,被捕食者的数量以表示.下图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法不正确的是( )
A.若在、时刻满足:,则
B.如果数量是先上升后下降的,那么的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数与捕食者数总和达到最大值时,捕食者的数量也会达到最大值
4.已知,,则的解析式为________.
5.函数,则__________(注明定义域)
6.已知一次函数满足,则=________.
7.已知函数,,.
(1)在图中画出函数,的图象;
(2)定义:,用表示,中的较小者,记为,请分别用图象法和解析式法表示函数.(注:图象法请在图中表示,本题中的单位长度请自己定义且标明)
8.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的表达式;
题组C 培优拔尖练
1.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
2.设函数,则满足的的取值范围是( )
A. B. C. D.
3.已知,则函数的值域为________.
4.若,则________.
5.已知函数,函数,其中
(1)若恒成立,求实数t的取值范围;
(2)若,
①求使得成立的x的取值范围;
②求在区间上的最大值.
6.已知函数,.
(1)求的表达式;
(2)求方程 解.
第5章 函数概念与性质
第02讲 函数的表示方法答案
课程标准 重难点
1.会根据不同的需要选择恰当的方法(如图象发、列表法、解析法)表示函数;2.理解函数图象的作用;3.会求函数的解析式. 1.函数的图象及其应用2.函数的解析式求法
一、函数的表示方法
1.任何一个函数都可以用解析法、列表法、图表法三种形式表示吗?
2.三种表示函数方法的优缺点:
二、分段函数
1.一般地,分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的 的函数.
2.分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是 .
3.作分段函数图象时,应分别作出每一段的图象.
4.分段函数是一个函数还是几个函数?
一、1. 不一定.并不是所有的函数都可以用解析式表示,不仅如此,图象法也不适用于所有函数,
如D(x)=列表法虽在理论上适用于所有函数,但对于自变量有无数个取值的情况,列表法只能表示函数的一个概况或片段.
二、1.对应关系 2.并集 空集 4. 分段函数是一个函数,而不是几个函数.
考法01 函数的三种表示方法
列表法、图象法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示.在用三种方法表示函数时要注意:①解析法必须注明函数的定义域;②列表法中选取的自变量要有代表性,应能反映定义域的特征;③图象法中要注意是否连线.
已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).
【解析】用图象法表示函数y=f(x),如图所示.
用列表法表示函数y=f(x),如表所示.
x 1 2 3 4
y -2 -3 -4 -5
【跟踪训练】已知函数f(x),g(x)分别由下表给出.
x 1 2 3
f(x) 2 1 1
x 1 2 3
g(x) 3 2 1
(1)f(g(1))=________;(2)若g(f(x))=2,则x=________.
【答案】(1)1 (2)1
【解析】(1)由表知g(1)=3,∴f(g(1))=f(3)=1.
(2)由表知g(2)=2,又因g(f(x))=2,得f(x)=2,再由表知x=1.
考法02 函数的图象及应用
描点法作函数图象的三个关注点
(1)画函数图象时首先关注函数的定义域,即在定义域内作图.
(2)图象是实线或实点,定义域外的部分有时可用虚线来衬托整个图象.
(3)要标出某些关键点,例如图象的顶点、端点、与坐标轴的交点等.要分清这些关键点是实心点还是空心圈.
注意:函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.
作出下列函数图象并指出其值域:
(1)y=1-x(x∈Z且|x|≤2);(2)y=2x2-4x-3(0≤x<3).
【解析】 (1)∵x∈Z且|x|≤2,∴x∈{-2,-1,0,1,2}.所以图象为一直线上的孤立点,如图所示.由图可知函数的值域为{3,2,1,0, -1}
(2)∵y=2(x-1)2-5,∴当x=0时,y=-3;
当x=3时,y=3;当x=1时,y=-5.所画函数图象如图所示.
由图可知函数的值域为[-5,3)
【跟踪训练】画出下列函数的图象:
(1)y=x+1(x≤0);(2)y=x2-2x(x>1,或x<-1).
【解析】 (1)y=x+1(x≤0)表示一条射线,图象如图①.
(2)y=x2-2x=(x-1)2-1(x>1,或x<-1)是抛物线y=x2-2x去掉-1≤x≤1之间的部分后剩余曲线.如图②.
考法03 函数的解析式
求函数解析式的4种常用求法
(1)配凑法:由已知条件f(g(x))=F(x),可将F(x)改写成关于g(x)的表达式,然后以x替代g(x),便得f(x)的表达式;
(2)待定系数法:若已知函数的类型(如一次函数、二次函数)可用待定系数法;
(3)换元法:已知复合函数f(g(x))的解析式,可用换元法,此时要注意新元的取值范围;
(4)解方程组法:已知关于f(x)与或f(-x)的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出f(x).
求下列函数的解析式:
(1)已知函数f(+1)=x+2,求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1)-f(x)=2x,求f(x).
(3)已知f(x)+2f(-x)=x2+2x,求f(x).
【解析】(1)方法一:(换元法)设t=+1,则x=(t-1)2(t≥1).
∴f(t)=(t-1)2+2(t-1)=t2-2t+1+2t-2=t2-1,∴f(x)=x2-1(x≥1).
方法二:(配凑法)∵x+2=()2+2+1-1=(+1)2-1,
∴f(+1)=(+1)2-1(+1≥1),∴f(x)=x2-1(x≥1).
(2)设f(x)=ax2+bx+c(a≠0).∵f(0)=1,∴c=1.
又∵f(x+1)-f(x)=2x,∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x,
整理,得2ax+(a+b)=2x.
由恒等式的性质,知上式中对应项的系数相等,
∴解得∴f(x)=x2-x+1.
(3)∵f(x)+2f(-x)=x2+2x,①
∴将x换成-x,得f(-x)+2f(x)=x2-2x.②
∴由①②得3f(x)=x2-6x,∴f(x)=x2-2x.
【跟踪训练】
变式1. (变条件)在例3(2)中,把条件换为“函数f(x)是一次函数,且f(f(x))=4x+8”,求f(x).
【解析】设f(x)=ax+b(a≠0),则f(f(x))=f(ax+b)=a(ax+b)+b=a2x+ab+b.
又f(f(x))=4x+8,∴a2x+ab+b=4x+8,
即,解得或∴f(x)=2x+或f(x)=-2x-8.
变式2. (变条件)在例3(3)中把条件换为“2f+f(x)=x(x≠0)”,求f(x)。
【解析】由f(x)+2f=x,令x=,得f+2f(x)=,
于是得关于f(x)与f的方程组解得f(x)=- (x≠0)。
题组A 基础过关练
1.图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时秒注满,设注水过程中,壶中水面高度为,注水时间为,则下面选项中最符合关于的函数图象的是( )
A. B.
C. D.
【答案】A
【解析】水壶的结构:低端与上端细、中间粗,
所以在注水恒定的情况下:
开始水的高度增加的快,中间增加的慢,最后水上升的速度又变快,
由图可知选项A符合,故选:A
2.如图,设有圆O和定点C,当从开始在平面上绕O匀速旋转(旋转角度不超过)时,它扫过圆内阴影部分面积S是时间t的函数,它的图像大致是如下哪一种( )
A.B.
C. D.
【答案】C
【解析】当直线从初始位置转到经过点的过程中阴影部分面积增加的越来越快,图像越来越“陡峭”;
从过点的位置转至结束时阴影部分面积增加的越来越慢,图像越来越“平缓”,
故选:C.
3.函数的大致图象为( )
A. B.
C. D.
【答案】D
【解析】因为,所以定义域为,关于原点对称,
因为,所以为奇函数,排除A、B,
又因为当时,,排除C.故选:D.
4.如图所示是一个无水游泳池,是一个四棱柱,游泳池是由一个长方体切掉一个三棱柱得到的.现在向泳池注水,如果进水速度是均匀的(单位时间内注入的水量不变),水面与的交点为,则的高度随时间变化的图象可能是( )
A. B. C. D.
【答案】A
【解析】由题意可知,当往游泳池内注水时,游泳池内的水呈“直棱柱”状,且直棱柱的高不变,
刚开始水面面积逐渐增大,水的高度增长得越来越慢,
当水面经过点后,水面的面积为定值,水的高度匀速增长,
故符合条件的函数图象为A选项中的图象.故选:A.
5.如图,在正方形中,点从点出发,沿向,以每个单位的速度在正方形的边上运动;点从点出发,沿方向,以每秒个单位的速度在正方形的边上运动.点与点同时出发,运动时间为(单位:秒),的面积为(规定共线时其面积为零,则点第一次到达点时,的图象为( )
A. B.
C. D.
【答案】A
【解析】根据题意,当,的面积为;
当,的面积为;
当,的面积为;
当,的面积为;
所以
所以根据分段函数的解析式即可得在区间上的函数图像为选项A.故选:A.
6.函数的部分图象大致为( )
A. B.
C. D.
【答案】A
【解析】因为,所以,
所以,且的定义域为关于原点对称,
所以为奇函数,排除B、D;
当时,,且,,所以,排除C,故选:A.
7.已知函数,若,则的取值集合是( )
A. B.
C. D.
【答案】A
【解析】若,可得,解得,(舍去);
若,可得=5,可得,与相矛盾,故舍去,
综上可得:.故选:A.
8.设,则的值为( )
A.16 B.18 C.21 D.24
【答案】B
【解析】因为,所以.
题组B 能力提升练
1.若函数,值域为,则( )
A. B.
C. D.
【答案】ACD
【解析】对于A,当,,则恒成立,
所以在上为单调递增函数,因为,故,故选项A正确;
且,故当时,值域为;
对于C,当时,则恒成立,
所以在上单调递减,所以,故,
又的值域为,所以,故,故选项C正确;
对于B,由选项C可知,,故,
所以,,
令,(),
所以,
当时,,则单调递增,
当时,,
此时,故选项B错误;
对于D,设,则,
令,则在恒成立,在上单调递增,
因此时,,,∴是减函数,
又,∴,即,
所以,则D正确.
故选:ACD.
2.在某种固体金属材料的耐高温实验中,温度随着时间变化的情况由微机记录后显示的图象如图所示,在实验过程中金属材料没有熔化.则下列结论正确的是( )
A.以后温度基本保持不变
B.前温度增加的速度越来越快
C.前温度增加的速度越来越慢
D.实验表明这种金属材料是耐高温的好材料
【答案】ACD
【解析】由图象可知前中温度增加,但是增加速度越来越慢,所以C对,B错.
以后温度图象是一条水平线,所以温度保持不变,A对,D对.故选:ACD.
3.假设存在两个物种,前者有充足的食物和生存空间,而后者仅以前者为食物,则我们称前者为被捕食者,后者为捕食者,现在我们来研究捕食者与被捕食者之间理想状态下的数学模型.假设捕食者的数量以表示,被捕食者的数量以表示.下图描述的是这两个物种随时间变化的数量关系,其中箭头方向为时间增加的方向.下列说法不正确的是( )
A.若在、时刻满足:,则
B.如果数量是先上升后下降的,那么的数量一定也是先上升后下降
C.被捕食者数量与捕食者数量不会同时到达最大值或最小值
D.被捕食者数与捕食者数总和达到最大值时,捕食者的数量也会达到最大值
【答案】ABD
【解析】由图可知,曲线中纵坐标相等时横坐标未必相等,故A不正确;
在曲线上半段中观察到是先上升后下降,而是不断变小的,故B不正确;
捕食者数量最大时是在图象最右端,最小值是在图象最左端,此时都不是被捕食者的数量的最值处,
同样当被捕食者的数量最大即图象最上端和最小即图象最下端时,也不是捕食者数量取最值的时候,
所以被捕食者数量和捕食者数量不会同时达到最大和最小值,故C正确;
当捕食者数量最大时在图象最右端,,,
此时二者总和,由图象可知存在点,,
,所以并不是被捕食者数量与捕食者数量总和达到最大值时,
被捕食者数量也会达到最大值,故D错误,故选:ABD.
4.已知,,则的解析式为________.
【答案】
【解析】由题知,,①;又,②;
由①②得,,
则,
故答案为:
5.函数,则__________(注明定义域)
【答案】
【解析】令,则,,
所以,,
所以.
故答案为:.
6.已知一次函数满足,则=________.
【答案】
【解析】设,则由,
得,即,故解得,
所以.
故答案为:.
7.已知函数,,.
(1)在图中画出函数,的图象;
(2)定义:,用表示,中的较小者,记为,请分别用图象法和解析式法表示函数.(注:图象法请在图中表示,本题中的单位长度请自己定义且标明)
【解析】(1),的图象如下图所示:
(2)当时,,则;
当时,,则;
当时,,则;
综上所述:.
图象如下图所示:
8.在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量R与管道半径r的四次方成正比.
(1)写出函数解析式(可带参数);
(2)假设气体在半径为3 cm的管道中的流量为400 cm3/s,求该气体通过半径为r cm的管道时,其流量R的表达式;
【解析】(1)由于流量R与管道半径r的四次方成正比,所以函数解析式为.
(2)由r=3 cm,R=400 cm3/s,得k·34=400,∴,∴流量R的表达式为.
题组C 培优拔尖练
1.已知函数,关于函数的结论正确的是( )
A.的定义域为 B.的值域为
C. D.若,则x的值是
E.的解集为
【答案】BD
【解析】由题意知函数的定义域为,故A错误;
当时,的取值范围是,当时,的取值范围是,因此的值域为,故B正确;
当时,,故C错误;
当时,,解得(舍去),当时,,解得
或(舍去),故D正确;
当时,,解得,当时,,解得,因此的解集为;故E错误.故选:BD.
2.设函数,则满足的的取值范围是( )
A. B. C. D.
【答案】D
【解析】因为,
所以,
,
(1)当时,,
若要,只需要 ,
即,
所以;
(2)当时,,
若要,
只需要,即,
所以.
综上所述,实数的取值范围是.
故选:D.
3.已知,则函数的值域为________.
【答案】
【解析】由题:,
,,所以的值域,
令,
函数的值域即,的值域,
,
当时,,当时,,
所以其值域为.
综上所述:函数的值域为.
故答案为:
4.若,则________.
【答案】
【解析】令,则,.
原式可变为①,
用代替t,则有②,
由①②消去得,
.故答案为:
5.已知函数,函数,其中
(1)若恒成立,求实数t的取值范围;
(2)若,
①求使得成立的x的取值范围;
②求在区间上的最大值.
【解析】(1)因为恒成立,所以恒成立,
所以恒成立,所以,解得,
所以;
(2)①当时,,所以,解得;
当时,,所以,
因为,所以,
所以无解,
综上所述:的取值范围是;
②由①可知:,
当时,,所以,所以;
当时,的对称轴为,所以,
且,所以,
令,所以,所以,
综上可知:.
6.已知函数,.
(1)求的表达式;
(2)求方程 解.
【解析】(1)当时,则,
,;
当时,则,
, ,;
当时,则,
, ,;
.
(2)当时,则,,
,,
,
,;
当时,则,,
,,
,无解;
当时,则,,
,,
,
,,
的解为,.
目标导航
知识精讲
能力拓展
例1
例2
例3
分层提分
目标导航
知识精讲
能力拓展
例1
例2
例3
分层提分
10 / 29
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
