广东省江门市棠下高级中学校2022-2023学年高二上学期期中考试数学试卷(含解析)
文档属性
| 名称 | 广东省江门市棠下高级中学校2022-2023学年高二上学期期中考试数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 599.9KB | ||
| 资源类型 | 教案 | ||
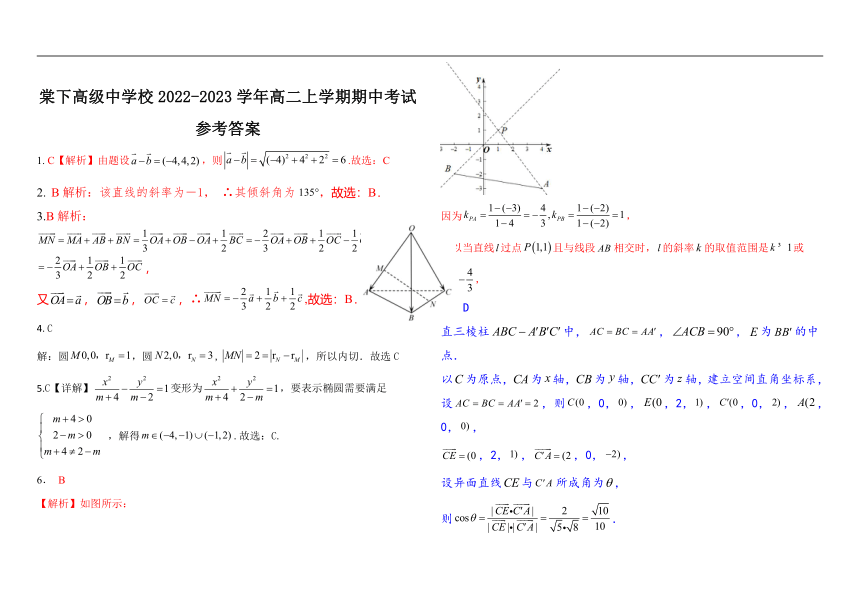
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-11 22:35:32 | ||
图片预览




文档简介
棠下高级中学校2022-2023学年高二上学期期中考试
数学
考试时间:120分钟
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.已知向量,,则( )
A. B.40 C.6 D.36
2. 直线的倾斜角为( )
A. 45° B. 135° C. 60° D. 120°
3.如图,在四面体OABC中,,,,点M在上,且满足,点N为BC的中点,则( )
A. B.
C. D.
4. 已知圆:与圆:,则两圆的位置关系是
A.相交 B.相离 C.内切 D.外切
5.若方程表示椭圆,则实数m的取值范围为( )
A. B. C. D.
6.设点,,直线过点且与线段相交,则的斜率的取值范围是( )
A.或 B.或 C. D.
7.直三棱柱ABC—A′B′C′中,AC=BC=AA′,∠ACB=90°,E为BB′的中点,异面直线CE与所成角的余弦值是( )
A. B. C.- D.
8.已知点P为圆:上任一点,点Q为
圆:上任一点,则的最小值为( )
A.1 B. C.2 D.4
二、多项选择题:本题共4小题,每小题4分,共16分.全部选对的得4分,有选错的得0分,部分选对的得2分.
9.已知直线l的方程为,则( )
A.直线l在x轴上的截距为2 B.直线l在y轴上的截距为3
C.直线l的倾斜角为锐角 D.过原点O且与l垂直的直线方程为
10. 已知椭圆的中心在坐标原点,离心率为,且椭圆上一点到椭圆的两个焦点的距离之和为,则椭圆的方程为( )
A. B. C. D.
11.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥ β B.⊥ α⊥ β
C.∥ l∥ α D.⊥ l∥ α
12. 已知圆心为的圆与点,则( )
A. 圆的半径为2 B. 点在圆外
C. 点与圆上任一点距离的最大值为
D. 点与圆上任一点距离的最小值为
三、填空题(每小题5分,共4小题20分)
13. 对任意实数,直线恒过定点,则该定点的坐标为_____.
14.已知平面的一个法向量为,平面的一个法向量,若,则的值为__________.
15.过点,且与椭圆有相同焦点的椭圆的标准方程为_______.
16.已知圆与圆相交于两点,则公共弦的长度是___________.
四、解答题(第17题10分,第18-22题各12分,共6小题70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)
已知三角形的三个顶点,,.
(1)求线段的中线所在直线方程;
(2)求边上的高所在的直线方程.
18. (12分)
(1)直线:,圆,若直线与圆交于A、两点,求弦的长.
(2)过点作与圆相切的直线l,求直线l的方程
19. (12分)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,
∠ BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥ 平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
20.(12分)已知圆:与圆:相交.
(1)求交点所在直线方程;
(2)若点P是圆C:上任意一点,求P点到(1)中交点所在直线距离的最大值和最小值.
21.(12分)
已知圆C过点A(1,2),B(2,1),且圆心C在直线上.P是圆C外的点,过点P的直线l交圆C于M,N两点.
(1)求圆C的方程;
(2)若点P的坐标为,探究:无论l的位置如何变化,|PM||PN|是否恒为定值?若是,求出该定值:若不是,请说明理由.
22. (12分)如图,在直角梯形ABCD中,ABDC,∠ ABC=90°,AB=2DC=2BC,
E为AB的中点,沿DE将△ ADE折起,使得点A到点P位置,且PE⊥ EB,M为PB的中点,N是BC上的动点(与点B,C不重合).
(1)求证:平面EMN⊥ 平面PBC;
(2)是否存在点N,使得二面角B﹣EN﹣M的余弦值?若存在,确定N点位置;若不存在,说明理由.
棠下高级中学校2022-2023学年高二上学期期中考试
参考答案
1. C【解析】由题设,则.故选:C
2. B解析:该直线的斜率为-1, ∴其倾斜角为135°,故选:B.
3.B解析:,
又,,,∴,故选:B.
4. C
解:圆,圆,,所以内切.故选C
5.C【详解】变形为,要表示椭圆需要满足 ,解得.故选:C.
6. B
【解析】如图所示:
因为,
所以当直线过点且与线段相交时,的斜率的取值范围是或,
7. D
直三棱柱中,,,为的中点.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
设,则,0,,,2,,,0,,,0,,
,2,,,0,,
设异面直线与所成角为,
则.
异面直线与所成角的余弦值为.
故选:.
8. A 解:由题知,圆半径为,圆心坐标为,圆半径为,圆心坐标为,所以两圆的位置关系为内含,所以,,
所以的最小值为.故选:A
9. BCD解析:在中,令,得,所以A不正确;令,得,所以B正确;因为直线l的斜率,所以直线l的倾斜角为锐角,故C正确;因为与l垂直的直线方程可设为,且直线过原点,所以,故D正确.故选BCD.
10. AC【详解】由椭圆的定义可得,可得,椭圆的离心率为,则,所以,.
若椭圆的焦点在轴上,则椭圆的方程为;
若椭圆的焦点在轴上,则椭圆的方程为.故选:AC.
11.【答案】AB
【详解】解:为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),
则∥ α∥β,⊥ α⊥β,∥ l⊥α,⊥ l∥α或l α.
因此AB正确.故选:AB.
12. BCD
【详解】依题意,圆:,则圆心,半径,A不正确;
因点,则,点在圆外,B正确;
因点在圆外,在圆上任取点P,则,当且仅当点P,C,A共线,且P在线段AC延长线上时取“=”,C正确;
在圆上任取点M,则,当且仅当点C,M,A共线,且M在线段CA上时取“=”,C正确.故选:BCD
13. 【详解】化为,
方程表示过点斜率为的直线方程,所以直线过定点.故答案为:.
14. 4解:,,存在实属使得
,所以的值为4.
15. 【详解】所求椭圆与椭圆的焦点相同,则其焦点在y轴上,半焦距c有c2=25-9=16,
设它的标准方程为 (a>b>0),于是得a2-b2=16,
又点(,-)在所求椭圆上,即,
联立两个方程得,即,解得b2=4,则a2=20,
所以所求椭圆的标准方程为.故答案为:
16. 解:由题意所在的直线方程为:,即,因为圆的圆心,半径为,
所以,圆心到直线的距离为1,所以.故答案为:
17.【答案】(1)(2).
【详解】(1)由题得BC的中点D的坐标为(2,-1),所以,
所以线段的中线AD所在直线方程为即.
(2)由题得,所以AB边上的高所在直线方程为,
即.
18.【答案】(1);(2)或
【小问1详解】
由题意知,圆心,圆心到直线:的距离,∴.
【小问2详解】
由题意,圆的圆心为,半径为1,∴在圆外,
当切线斜率不存在时,切线方程为,所以是其中一条切线;
当切线斜率存在时,设切线方程为,则,可得,
∴切线方程为.综上,切线方程为或.
19.(1)见解析(2)
【详解】(1)连接ME,BC , ∵ M,E分别为B1B,BC的中点 , ∴
又∵,∴A1DCB1是平行四边形
∴
∴
∴NDEM是平行四边形
∴NM∥DE
又NM平面C1DE
∴NM∥平面C1DE
(2)由题意得DE与BC垂直,所以DE与AD垂直:以D为原点,DA,DE,DD1三边分别为x,y,z轴,建立空间坐标系O-xyz
则A(2,0,0),A1(2,0,4),M(1,,2)
设平面A1MD的法向量为
则
∴
解得
又
∴
∴AM与平面A1MD所成角的正弦值.
20. 【答案】(1);(2)最大值,最小值.
【详解】(1)由已知:圆:,圆:,
故交点所在直线的方程为:,
即,故交点所在直线的方程为.
(2)由圆C:知,圆心为,半径为1,
所以圆心到直线距离,
所以圆上点到直线的,.
21.【解析】(1)由于圆心在,故设圆的方程为,将A(1,2),B(2,1)代入可得,解得,
所以圆的方程为:
(2)当直线轴时,,
当直线有斜率时,设其方程为:,
联立直线与圆的方程,消元得,
设,则,,
由于点在圆外,所以,
因此,
综上,无论l的位置如何变化,,为定值.
22.解:(1)证明:由PE⊥EB,PE⊥ED,EB∩ED=E,
所以PE⊥平面EBCD,又BC 平面EBCD,
故PE⊥BC,又BC⊥BE,故BC⊥平面PEB,
EM 平面PEB,故EM⊥BC,
又等腰三角形PEB,EM⊥PB,
BC∩PB=B,故EM⊥平面PBC,EM 平面EMN,
故平面EMN⊥平面PBC;
(2)假设存在点N,使得二面角B﹣EN﹣M的余弦值.
以E为原点,分别为x,y,z轴建立空间直角坐标系,
设PE=EB=2,设N(2,m,0),B(2,0,0),D(0,2,0),
P(0,0,2),C(2,2,0),M(1,0,1),
,,,
设平面EMN的法向量为,
由,令,得,
平面BEN的一个法向量为,
故,
解得:m=1,
故存在N为BC的中点.
数学
考试时间:120分钟
一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个备选项中,只有一项是符合题目要求的.)
1.已知向量,,则( )
A. B.40 C.6 D.36
2. 直线的倾斜角为( )
A. 45° B. 135° C. 60° D. 120°
3.如图,在四面体OABC中,,,,点M在上,且满足,点N为BC的中点,则( )
A. B.
C. D.
4. 已知圆:与圆:,则两圆的位置关系是
A.相交 B.相离 C.内切 D.外切
5.若方程表示椭圆,则实数m的取值范围为( )
A. B. C. D.
6.设点,,直线过点且与线段相交,则的斜率的取值范围是( )
A.或 B.或 C. D.
7.直三棱柱ABC—A′B′C′中,AC=BC=AA′,∠ACB=90°,E为BB′的中点,异面直线CE与所成角的余弦值是( )
A. B. C.- D.
8.已知点P为圆:上任一点,点Q为
圆:上任一点,则的最小值为( )
A.1 B. C.2 D.4
二、多项选择题:本题共4小题,每小题4分,共16分.全部选对的得4分,有选错的得0分,部分选对的得2分.
9.已知直线l的方程为,则( )
A.直线l在x轴上的截距为2 B.直线l在y轴上的截距为3
C.直线l的倾斜角为锐角 D.过原点O且与l垂直的直线方程为
10. 已知椭圆的中心在坐标原点,离心率为,且椭圆上一点到椭圆的两个焦点的距离之和为,则椭圆的方程为( )
A. B. C. D.
11.已知为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),那么下列选项中,正确的是( )
A.∥ α∥ β B.⊥ α⊥ β
C.∥ l∥ α D.⊥ l∥ α
12. 已知圆心为的圆与点,则( )
A. 圆的半径为2 B. 点在圆外
C. 点与圆上任一点距离的最大值为
D. 点与圆上任一点距离的最小值为
三、填空题(每小题5分,共4小题20分)
13. 对任意实数,直线恒过定点,则该定点的坐标为_____.
14.已知平面的一个法向量为,平面的一个法向量,若,则的值为__________.
15.过点,且与椭圆有相同焦点的椭圆的标准方程为_______.
16.已知圆与圆相交于两点,则公共弦的长度是___________.
四、解答题(第17题10分,第18-22题各12分,共6小题70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)
已知三角形的三个顶点,,.
(1)求线段的中线所在直线方程;
(2)求边上的高所在的直线方程.
18. (12分)
(1)直线:,圆,若直线与圆交于A、两点,求弦的长.
(2)过点作与圆相切的直线l,求直线l的方程
19. (12分)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,
∠ BAD=60°, E,M,N分别是BC,BB1,A1D的中点.
(1)证明:MN∥ 平面C1DE;
(2)求AM与平面A1MD所成角的正弦值.
20.(12分)已知圆:与圆:相交.
(1)求交点所在直线方程;
(2)若点P是圆C:上任意一点,求P点到(1)中交点所在直线距离的最大值和最小值.
21.(12分)
已知圆C过点A(1,2),B(2,1),且圆心C在直线上.P是圆C外的点,过点P的直线l交圆C于M,N两点.
(1)求圆C的方程;
(2)若点P的坐标为,探究:无论l的位置如何变化,|PM||PN|是否恒为定值?若是,求出该定值:若不是,请说明理由.
22. (12分)如图,在直角梯形ABCD中,ABDC,∠ ABC=90°,AB=2DC=2BC,
E为AB的中点,沿DE将△ ADE折起,使得点A到点P位置,且PE⊥ EB,M为PB的中点,N是BC上的动点(与点B,C不重合).
(1)求证:平面EMN⊥ 平面PBC;
(2)是否存在点N,使得二面角B﹣EN﹣M的余弦值?若存在,确定N点位置;若不存在,说明理由.
棠下高级中学校2022-2023学年高二上学期期中考试
参考答案
1. C【解析】由题设,则.故选:C
2. B解析:该直线的斜率为-1, ∴其倾斜角为135°,故选:B.
3.B解析:,
又,,,∴,故选:B.
4. C
解:圆,圆,,所以内切.故选C
5.C【详解】变形为,要表示椭圆需要满足 ,解得.故选:C.
6. B
【解析】如图所示:
因为,
所以当直线过点且与线段相交时,的斜率的取值范围是或,
7. D
直三棱柱中,,,为的中点.
以为原点,为轴,为轴,为轴,建立空间直角坐标系,
设,则,0,,,2,,,0,,,0,,
,2,,,0,,
设异面直线与所成角为,
则.
异面直线与所成角的余弦值为.
故选:.
8. A 解:由题知,圆半径为,圆心坐标为,圆半径为,圆心坐标为,所以两圆的位置关系为内含,所以,,
所以的最小值为.故选:A
9. BCD解析:在中,令,得,所以A不正确;令,得,所以B正确;因为直线l的斜率,所以直线l的倾斜角为锐角,故C正确;因为与l垂直的直线方程可设为,且直线过原点,所以,故D正确.故选BCD.
10. AC【详解】由椭圆的定义可得,可得,椭圆的离心率为,则,所以,.
若椭圆的焦点在轴上,则椭圆的方程为;
若椭圆的焦点在轴上,则椭圆的方程为.故选:AC.
11.【答案】AB
【详解】解:为直线l的方向向量,,分别为平面α,β的法向量(α,β不重合),
则∥ α∥β,⊥ α⊥β,∥ l⊥α,⊥ l∥α或l α.
因此AB正确.故选:AB.
12. BCD
【详解】依题意,圆:,则圆心,半径,A不正确;
因点,则,点在圆外,B正确;
因点在圆外,在圆上任取点P,则,当且仅当点P,C,A共线,且P在线段AC延长线上时取“=”,C正确;
在圆上任取点M,则,当且仅当点C,M,A共线,且M在线段CA上时取“=”,C正确.故选:BCD
13. 【详解】化为,
方程表示过点斜率为的直线方程,所以直线过定点.故答案为:.
14. 4解:,,存在实属使得
,所以的值为4.
15. 【详解】所求椭圆与椭圆的焦点相同,则其焦点在y轴上,半焦距c有c2=25-9=16,
设它的标准方程为 (a>b>0),于是得a2-b2=16,
又点(,-)在所求椭圆上,即,
联立两个方程得,即,解得b2=4,则a2=20,
所以所求椭圆的标准方程为.故答案为:
16. 解:由题意所在的直线方程为:,即,因为圆的圆心,半径为,
所以,圆心到直线的距离为1,所以.故答案为:
17.【答案】(1)(2).
【详解】(1)由题得BC的中点D的坐标为(2,-1),所以,
所以线段的中线AD所在直线方程为即.
(2)由题得,所以AB边上的高所在直线方程为,
即.
18.【答案】(1);(2)或
【小问1详解】
由题意知,圆心,圆心到直线:的距离,∴.
【小问2详解】
由题意,圆的圆心为,半径为1,∴在圆外,
当切线斜率不存在时,切线方程为,所以是其中一条切线;
当切线斜率存在时,设切线方程为,则,可得,
∴切线方程为.综上,切线方程为或.
19.(1)见解析(2)
【详解】(1)连接ME,BC , ∵ M,E分别为B1B,BC的中点 , ∴
又∵,∴A1DCB1是平行四边形
∴
∴
∴NDEM是平行四边形
∴NM∥DE
又NM平面C1DE
∴NM∥平面C1DE
(2)由题意得DE与BC垂直,所以DE与AD垂直:以D为原点,DA,DE,DD1三边分别为x,y,z轴,建立空间坐标系O-xyz
则A(2,0,0),A1(2,0,4),M(1,,2)
设平面A1MD的法向量为
则
∴
解得
又
∴
∴AM与平面A1MD所成角的正弦值.
20. 【答案】(1);(2)最大值,最小值.
【详解】(1)由已知:圆:,圆:,
故交点所在直线的方程为:,
即,故交点所在直线的方程为.
(2)由圆C:知,圆心为,半径为1,
所以圆心到直线距离,
所以圆上点到直线的,.
21.【解析】(1)由于圆心在,故设圆的方程为,将A(1,2),B(2,1)代入可得,解得,
所以圆的方程为:
(2)当直线轴时,,
当直线有斜率时,设其方程为:,
联立直线与圆的方程,消元得,
设,则,,
由于点在圆外,所以,
因此,
综上,无论l的位置如何变化,,为定值.
22.解:(1)证明:由PE⊥EB,PE⊥ED,EB∩ED=E,
所以PE⊥平面EBCD,又BC 平面EBCD,
故PE⊥BC,又BC⊥BE,故BC⊥平面PEB,
EM 平面PEB,故EM⊥BC,
又等腰三角形PEB,EM⊥PB,
BC∩PB=B,故EM⊥平面PBC,EM 平面EMN,
故平面EMN⊥平面PBC;
(2)假设存在点N,使得二面角B﹣EN﹣M的余弦值.
以E为原点,分别为x,y,z轴建立空间直角坐标系,
设PE=EB=2,设N(2,m,0),B(2,0,0),D(0,2,0),
P(0,0,2),C(2,2,0),M(1,0,1),
,,,
设平面EMN的法向量为,
由,令,得,
平面BEN的一个法向量为,
故,
解得:m=1,
故存在N为BC的中点.
同课章节目录
