2021-2022学年河北省各地冀教版数学九年级上学期期末试题选编 第二十九章 直线与圆的位置关系 综合复习题(含解析)
文档属性
| 名称 | 2021-2022学年河北省各地冀教版数学九年级上学期期末试题选编 第二十九章 直线与圆的位置关系 综合复习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 00:00:00 | ||
图片预览


文档简介
第二十九章 直线与圆的位置关系 综合复习题
一、单选题
1.(2022·河北邯郸·九年级期末)平面内有两点P,O,⊙O的半径为5,若,则点P与⊙O的位置关系是( )
A.圆内 B.圆上 C.圆外 D.圆上或圆外
2.(2022·河北邢台·九年级期末)已知⊙O的半径为3,平面内有一点到圆心O的距离为5,则此点可能是( )
A.P点 B.Q点 C.M点 D.N点
3.(2022·河北承德·九年级期末)在中,,,以A为圆心2.5为半径作圆.下列结论中正确的是( )
A.直线BC与圆O相切 B.直线BC与相离 C.点B在圆内 D.点C在圆上
4.(2022·河北唐山·九年级期末)内接于,过点A作直线EF,已知,根据弦AB的变化,两人分别探究直线EF与的位置关系:
甲:如图1,当弦AB过点O时,EF与相切;
乙:如图2,当弦AB不过点O时,EF也与相切;
下列判断正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.甲乙都对 D.甲乙都不对
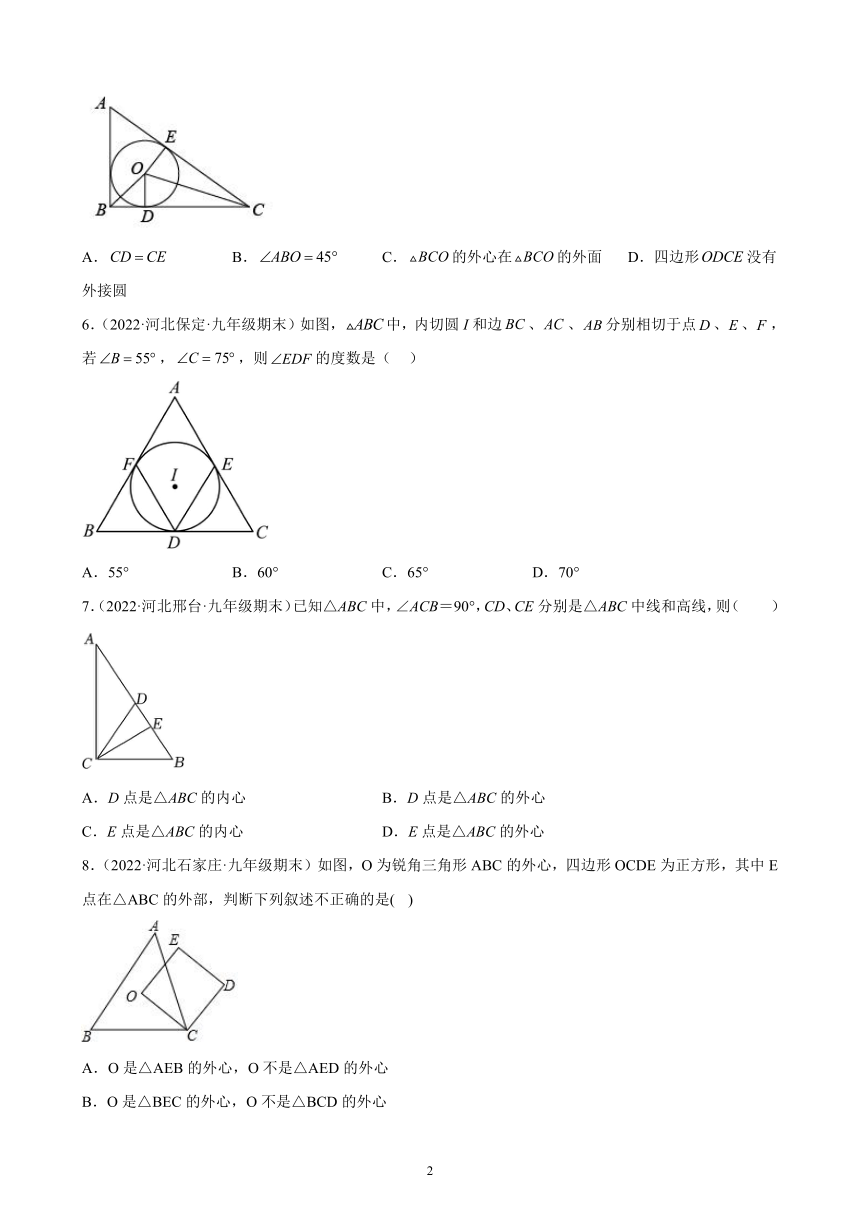
5.(2022·河北沧州·九年级期末)如图,是的内切圆,点,是切点,则下列说法不正确的是( )
A. B. C.的外心在的外面 D.四边形没有外接圆
6.(2022·河北保定·九年级期末)如图,中,内切圆I和边、、分别相切于点、、,若,,则的度数是( )
A.55° B.60° C.65° D.70°
7.(2022·河北邢台·九年级期末)已知△ABC中,∠ACB=90°,CD、CE分别是△ABC中线和高线,则( )
A.D点是△ABC的内心 B.D点是△ABC的外心
C.E点是△ABC的内心 D.E点是△ABC的外心
8.(2022·河北石家庄·九年级期末)如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )
A.O是△AEB的外心,O不是△AED的外心
B.O是△BEC的外心,O不是△BCD的外心
C.O是△AEC的外心,O不是△BCD的外心
D.O是△ADB的外心,O不是△ADC的外心
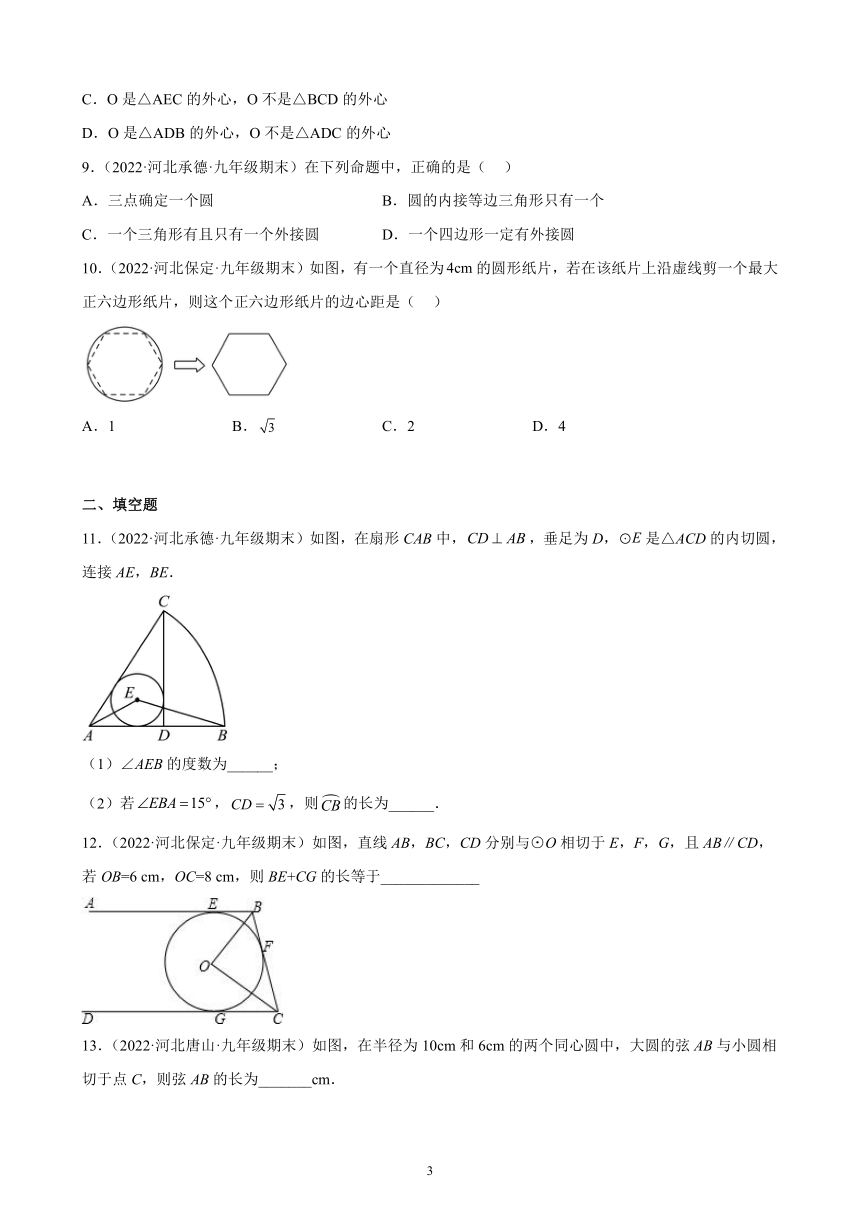
9.(2022·河北承德·九年级期末)在下列命题中,正确的是( )
A.三点确定一个圆 B.圆的内接等边三角形只有一个
C.一个三角形有且只有一个外接圆 D.一个四边形一定有外接圆
10.(2022·河北保定·九年级期末)如图,有一个直径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( )
A.1 B. C.2 D.4
二、填空题
11.(2022·河北承德·九年级期末)如图,在扇形CAB中,,垂足为D,是△ACD的内切圆,连接AE,BE.
(1)∠AEB的度数为______;
(2)若,,则的长为______.
12.(2022·河北保定·九年级期末)如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6 cm,OC=8 cm,则BE+CG的长等于_____________
13.(2022·河北唐山·九年级期末)如图,在半径为10cm和6cm的两个同心圆中,大圆的弦AB与小圆相切于点C,则弦AB的长为_______cm.
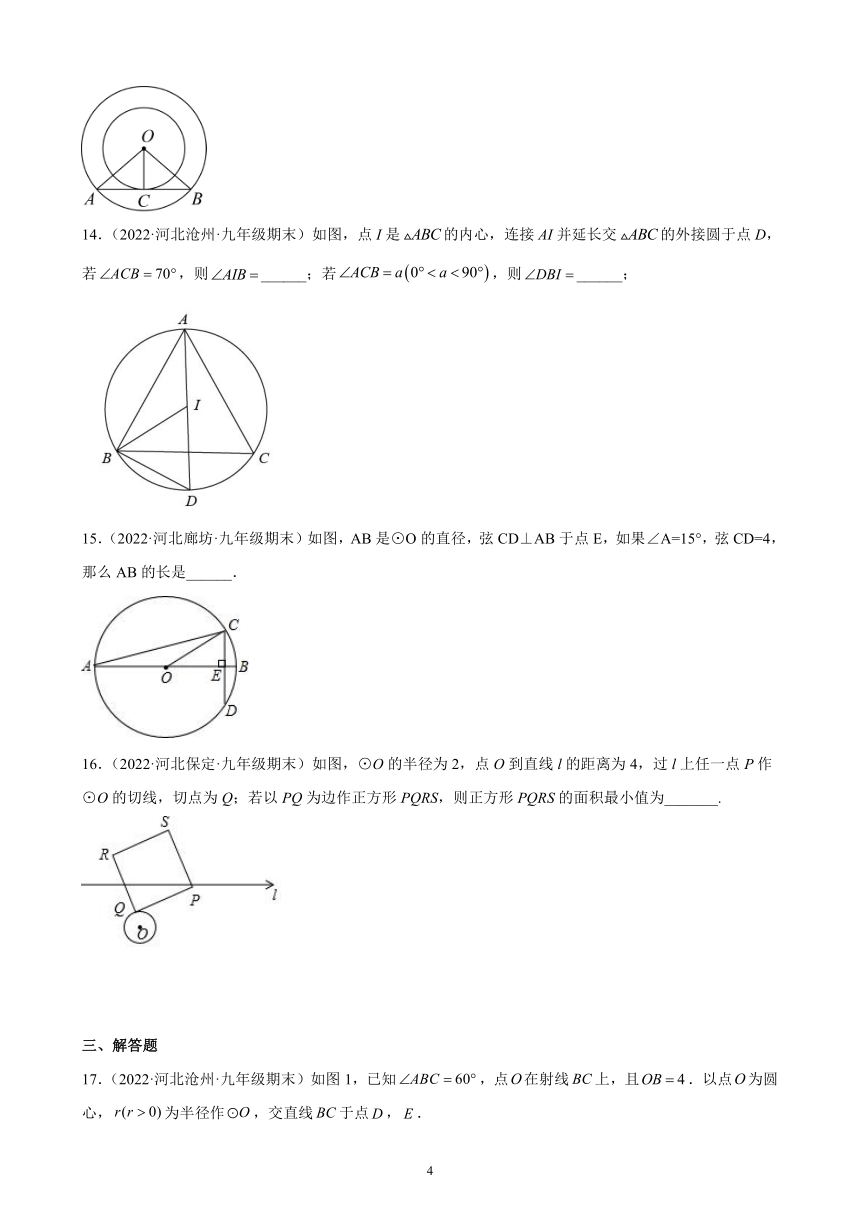
14.(2022·河北沧州·九年级期末)如图,点I是的内心,连接AI并延长交的外接圆于点D, 若,则______;若,则______;
15.(2022·河北廊坊·九年级期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4,那么AB的长是______.
16.(2022·河北保定·九年级期末)如图,⊙O的半径为2,点O到直线l的距离为4,过l上任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小值为_______.
三、解答题
17.(2022·河北沧州·九年级期末)如图1,已知,点在射线上,且.以点为圆心,为半径作,交直线于点,.
(1)当与只有两个交点时,的取值范围是________;
(2)当时,将射线绕点按顺时针方向旋转.
①当为多少时,射线与相切;
②如图2,射线与交于,两点,若,求阴影部分的面积.
18.(2022·河北唐山·九年级期末)如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.
(1)求证:EF是⊙O的切线;
(2)若AD=1,求DC的长;
(3)在(2)的条件下,求图中阴影部分的面积.
19.(2022·河北石家庄·九年级期末)如图,△ABC中,AB=AC=10cm.BC=16cm,动点P从点C出发沿线段CB以2cm/s的速度向点B运动,同时动点Q从点B出发沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止运动,设运动时间为t(单位:s),以点Q为圆心,BQ长为半径的⊙Q与射线BA、线段BC分别交于点D,E,连接DP.
(1)当t为何值时,线段DP与⊙Q相切;
(2)若⊙Q与线段DP只有一个公共点,求t的取值范围;
(3)当△APC是等腰三角形时,直接写出t的值.
20.(2022·河北石家庄·九年级期末)如图,在中,,以点O为圆心、2为半径画圆,过点A作的切线,切点为P,连接.将绕点O按逆时针方向旋转到时,连接.设旋转角为.
(1)当时,求证:是的切线;
(2)当与相切时,求旋转角和点H运动路径的长;
(3)当面积最大时,请直接写出此时点H到的距离.
21.(2022·河北邢台·九年级期末)已知正六边形ABCDEF的中心为O,半径OA=6.
(1)求正六边形的边长;
(2)以A为圆心,AF为半径画弧BF,求.
22.(2022·河北承德·九年级期末)如图,,,,,点在对角线上运动,以为圆心,为半径作.
(1)当点在上时,______,此时与的位置关系是______;
(2)当与边相切时,求的长;
(3)直接写出与的边有公共点时的取值范围.
23.(2022·河北廊坊·九年级期末)如图,中,,,过点,,的弧的半径为,点在上.,切线交的延长线于点.
(1)求的长;
(2)求的度数.
24.(2022·河北保定·九年级期末)如图,为直径,点C在上,平分,,垂足为E.
(1)求证:为切线.
(2)若,,求的半径.
25.(2022·河北邢台·九年级期末)如图所示的四边形ABCD是边长为16的正方形,O是边AD上的一个动点,且8(1)求证:.
(2)当DM=8时,求OA,CN的长.
26.(2022·河北承德·九年级期末)如图,在矩形ABCD中,,,点P从点B出发,沿BA边向终点A以每秒1cm的速度运动,同时点Q从点C出发沿C-B-A向终点A以每秒3cm的速度运动,Q追上P时停止运动,设运动时间为t秒.解答下列问题:
(1)当______时点Q与点B重合,当______时点Q追上点P;
(2)当Q在BC边上时,求t为何值时PQ的长为cm;
(3)作为P为圆心,PQ长为半径作,是否存在这样的t值,使正好与的一边(或边所在的直线)相切?若存在直接写出t的值,若不存在,请说明理由.
参考答案:
1.C
【解析】根据点到圆心的距离小于半径即可判断点P在⊙O的内部.
∵⊙O的半径为5,PO=6,
∴点P到圆心O的距离大于半径,
∴点P在⊙O的外部,
故选C.
本题考查了点与圆的位置关系,理解点与圆的位置关系是解题的关键.
2.D
【解析】根据点到圆心O的距离大于半径,可判定出点在圆外,即可得到答案.
∵平面内有一点到圆心O的距离为5,5>3.
∴该点在圆外,
∴点N符合要求.
故选:D.
本题考查了点与圆的位置关系,根据点到圆心距离与半径的大小关系可作出判断.
3.B
【解析】过A点作AH⊥BC于H,如图,利用等腰三角形的性质得到BH=CH=BC=4,则利用勾股定理可计算出AH=3,然后根据直线与圆的位置关系的判定方法对A选项和B选项进行判断;根据点与圆的位置关系对C选项和D选项进行判断.
解:过A点作AH⊥BC于H,如图,
∵AB=AC,
∴BH=CH=BC=4,
在Rt△ABH中,,
∵AH⊥BC,AH=3>2.5,
∴直线BC与⊙A相离,所以A选项不符合题意,B选项符合题意.
∵AB=5>2.5,
∴B点在⊙A外,所以C选项不符合题意;
∵AC=5>2.5,
∴C点在⊙A外,所以D选项不符合题意;
故选:B.
本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,若直线l和⊙O相交 d<r;直线l和⊙O相切 d=r;直线l和⊙O相离 d>r.也考查了点与圆的位置关系和等腰三角形的性质.
4.C
【解析】甲:根据直径推出,推出,根据切线判定推出即可;
乙:作直径,连接,推出,求出,根据切线的判定推出即可.
解:甲:是的直径,
,
,
,
,
,
是半径,
是的切线;
乙:作直径,连接,
即(在同圆或等圆中,同弧所对的圆周角相等),
,
,
是的直径,
,
,
,
,
是半径,
是的切线.
故选:C.
考查了切线的判定,圆周角定理,三角形的内角和定理等知识点,注意:经过半径的外端且垂直于半径的直线是圆的切线,直径所对的圆周角是直角,正确应用定理等知识是解决问题的关键.
5.D
【解析】根据切线的定理可判断A,作于,可证四边形为正方形,即可判断B;根据为钝角三角形即可判断C;根据四边形的对角即可判断D.
解: ,是切点,
根据切线定理可知,故选项A正确,不满足题意;
作交于,
是的内切圆,
为切点,,
为切点,
,
四边形为正方形,
,故选项B正确,不满足题意;
由题可知为钝角三角形,
的外心在的外面,故选项C正确,不满足题意;
,
,
,
四边形有外接圆,故选项D错误,满足题意.
故选:D.
本题主要考查切线的性质,正方形的判定与性质,三角形的外心,四边形的外接圆,掌握相关定理与概念是解题的关键.
6.C
【解析】连接IE、IF,如图,根据切线的性质得到,利用四边形的内角和得到,再利用圆周角定理得到,然后根据三角形内角和求出,从而可计算出.
连接IE、IF,如图,
∵内切圆I和边AC、AB分别相切于点E、F,
∴,,
∴,
∵,
∴,
∵,,
∴,
∴,
故选:C.
本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆;三角形的内心与三角形顶点的连线平分这个内角.也考查了切线的性质.解题关键是根据三角形的内切圆与内心的性质作出合适的辅助线.
7.B
【解析】根据直角三角形斜边上的中线等于斜边的一半,可得是△ABC的外心,据此即可求解.
解:在△ABC中,∠ACB=90°,
∵CD是△ABC中线,
∴D点是△ABC的外心.
故选:B.
本题考查了三角形的外心,直角三角形斜边上的中线等于斜边的一半,掌握以上知识是解题的关键.
8.C
【解析】根据三角形的外心得出OA=OC=OB,根据正方形的性质得出OA=OC<OD,求出OA=OB=OC=OE≠OD,再逐个判断即可
连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OA=OC<OD,
∴OA=OB=OC=OE≠OD,
∴OA=OE≠OD,即O不是△AED的外心,
OA=OE=OB,即O是△AEB的外心,
OA=OC=OE,即O是△ACE的外心,
OB=OA≠OD,即O不是△ABD的外心,
故选C.
本题考查了正方形的性质和三角形的外心与外接圆,能熟记知识点的内容是解此题的关键,注意:三角形的外心到三个顶点的距离相等,正方形的四边都相等.
9.C
【解析】利用确定圆的条件、圆内接三角形的定义、三角形外接圆的定义,四边形外接圆的定义分别判断后即可确定正确的选项.
解:A、不在同一直线上的三点确定一个圆,故错误;
B、圆内接等边三角形有无数个,故错误;
C、一个三角形有且只有一个外接圆,正确;
D、并不是所有的四边形都有外接圆,故错误,
故选:C.
本题考查了确定圆的条件、圆内接三角形的定义、三角形外接圆的定义,四边形外接圆的定义等知识,难度不大.
10.B
【解析】连接OA、OB,根据圆内接正六边形的性质得到△AOB是等边三角形,作OC⊥AB于C,求得∠AOC= 30°,由OA=2cm,得到AC=1cm,根据勾股定理求出OC即可.
如图,连接OA、OB,则△AOB是等边三角形,作OC⊥AB于C,
∵△AOB是等边三角形,
∴∠OAB= 60°,
∴∠AOC= 30°,
∵OA=2cm,
∴AC=1cm,
OC=,
故选:B.
此题考查圆内接正六边形的性质,等边三角形的性质,勾股定理,直角三角形30度角所对的直角边等于斜边的一半的性质,熟记圆内接正六边形的性质是解题的关键.
11. 135°
【解析】(1)如图,连接EC.首先证明∠AEC=135°,再证明△EAC≌△EAB即可解决问题;
(2)先利用已知求得∠CAB的度数,然后在直角三角形ACD中求得AC的长,最后利用弧长公即可求解.
解:(1)如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180° (∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
(2)∵,∠AEB=135°,
∴ ,
∴,
∵,,
∴中,,
解得,
∴,
故答案为:
本题考查三角形的内心、全等三角形的判定和性质,弧长公式等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
12.10cm##10厘米
【解析】根据平行线的性质以及切线长定理,即可证明∠BOC=90°,再根据勾股定理即可求得BC的长,再结合切线长定理即可求解.
解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵直线AB,BC,CD分别与⊙O相切于E,F,G,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=(∠ABC+∠BCD)=90°,
∴∠BOC=90°,
在Rt△BOC中,
BC==10,
∴BE+CG=10(cm).
故答案为:10cm.
此题主要是考查了切线长定理.熟记从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角是解决问题的关键.
13.16
【解析】根据切线的性质得到OC⊥AB,根据垂径定理得到AC=AB,根据勾股定理计算,得到答案.
解:∵AB是小圆O的切线,
∴OC⊥AB,
∵AB是大圆O的弦,
∴AC=AB,
在Rt△AOC中,AC===8(cm),
则AB=2AC=16(cm),
故答案为:16.
本题考查的是切线的性质、垂径定理和勾股定理的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.
14. 125°
【解析】根据三角形内心的性质可得进而求得,再根据三角形内角和定理即可得到答案;
先求出,再根据外角的性质即可得到,再由三角形的内角和定理得出的度数即可.
点I是的内心
在中,
故答案为:125°;
点I是的内心
在中,
故答案为:.
本题考查了三角形外接圆与三角形的内心的性质、三角形的内角和定理、外角的性质,同弧所对的圆周角相等这些知识点,熟练掌握并能够运用是解题的关键.
15.8
【解析】首先根据圆的性质得出∠COB=30°,然后根据垂径定理得出CE=2,∠OEC=90°,解直角三角形得出OC,进而得出AB.
∵∠A=15°,
∴∠COB=30°,
∵AB是⊙O的直径,弦CD⊥AB于点E,弦CD=4,
∴CE=2,∠OEC=90°
∵∠COE=30°,
∴OC=2CE=4,
∴AB=2OC=8,
故答案为:8.
此题主要考查垂径定理以及含30°角直角三角形的性质,熟练掌握,即可解题.
16.12
【解析】连接OQ、OP,如图,根据切线的性质得OQ⊥PQ,则利用勾股定理得到PQ2=OP2﹣OQ2=OP2﹣4,也是判断OP取最小值时,PQ2的值最小,此时正方形PQRS的面积有最小值,根据垂线段最短得到OP的最小值为4,于是得到PQ2的最小值,从而确定正方形PQRS的面积的最小值.
解:连接OQ、OP,如图,
∵PQ为切线,
∴OQ⊥PQ,
在Rt△OPQ中,PQ2=OP2﹣OQ2=OP2﹣4,
当OP取最小值时,PQ2的值最小,此时正方形PQRS的面积有最小值,
而当OP⊥l时,OP取最小值,
∴OP的最小值为4,
∴PQ2的最小值为16﹣4=12,
∴正方形PQRS的面积最小值为12.
故答案为12.
本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.充分利用垂线段最短解决最小值问题.
17.(1))0<r<2或r>4
(2)①当α为15°或105°时,射线BA与⊙O相切;②S阴影=2π-4
【解析】(1)画出图形分: 当时,当时,时,时,时,五种情况讨论,即可得出答案;
(2)①分当射线BA在射线BC的上方与⊙O相切时和当射线BA在射线BC的下方与⊙O相切时,进行求解即可得出答案;
② 如图3,连接OM,ON,过点O作OQ⊥MN于点Q,由垂径定理可得出MQ=NQ=MN=,即可推得:∠MOQ=,故圆心角,由即可得出答案.
(1)
若与相切时,设切点为F,连接,如图:
则,
在中,,,
∴,
∴,
当时,与刚好有个交点,
∴当时, 如图:与只有两个交点;
当,即时,如图,与有个交点;
当即时,如图与有个交点;
当即时,如图,与有两个交点;
综上所述,当与只有两个交点时,的取值范围是或,
故答案为:或;
(2)
①如图1,当射线BA在射线BC的上方与⊙O相切时,设切点为P,连接OP.
∵OB=,OP=,
∴sinB==,
∴,
.
如图2,当射线BA在射线BC的下方与⊙O相切时,设切点为P,连接OP,
∵OB=,OP=,
∴sinB==,
∴,
∴.
综上所述,当α为或时,射线BA与⊙O相切;
②如图3,连接OM,ON,过点O作OQ⊥MN于点Q,
∴MQ=NQ=MN=.
∵OM=,
∴,
∴,
∴,
∴.
本题考查了直线与圆的位置关系,勾股定理,锐角三角函数、求弓形面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用特殊位置解决问题.
18.(1)见解析
(2)
(3)
【解析】(1)连接OC,由OB=OC,利用等边对等角得到∠BCO=∠B,由∠ACD=∠B,得到∠ACD+∠OCA=90°,得到OC垂直于EF,即可得到EF为圆O的切线;
(2)证明Rt△ABC∽Rt△ACD,可求出AC=2,由勾股定理求出CD的长即可;
(3)先证明△OAC为等边三角形,求出∠AOC=60°,即可由S阴影=S梯形ADCO-S扇形OAC求出答案.
(1)证明:连接OC,∵AB为⊙O直径,∴∠ACB=90°,∴∠B+∠BAC=90°∵OC=OA,∴∠OCA=∠OAC∵∠ACD=∠B,∴∠OCD=∠OCA+∠ACD=90°,即EF⊥OC∴EF是⊙O的切线
(2)解:∵AB是⊙O直径,∴∠ACB==90°,∵AD⊥EF于点D,∴∠∠ADC=90°,∴∠ADC=∠BCA,∵∠ACD=∠B,∴△ACD∽△ABC∴,∵AD=1,AB=4∴,∴AC=2∴
(3)解:∵AB=4,∴OC=OA=AB=2,由(2)知:AC=2,∴OC=OA=AC=2,∴△ACO为等边三角形,∴∠AOC=60°,由(2)知:CD=,AD=1∴S阴影=S梯形ADCO-S扇形OAC==.
本题是圆的综合题,考查了切线的判定,等腰三角形的性质,圆周角定理,相似三角形的判定与性质,等边三角形的判定与性质,勾股定理以及扇形面积的计算,熟练掌握圆的基础知识是解本题的关键.
19.(1)当t时,线段DP与⊙Q相切;
(2)0<t或;
(3)或5或8.
【解析】(1)过点A作AN⊥BC于点N,则BNcm,由线段DP与⊙Q相切,则∠BDP=∠BNA=90°,利用△BDP∽△BNA,得,代入即可求出t的值;
(2)分两种情形:出发后到DP与圆相切时,⊙Q与线段DP只有一个公共点,得0<t,当点P与点E重合后,点P在⊙Q内,此时⊙Q与线段DP只有一个公共点,当点P与点E重合时,,可解决问题;
(3)分AP=AC,PPC,CA=CP三种情形,分别画出图形,即可解决问题.
(1)
解:由题意得:CP=2tcm,BD=2tcm,则BP=(16﹣2t)cm,
过点A作AN⊥BC于点N,如图1,
则BNcm,
∵线段DP与⊙Q相切,
∴PD⊥BD,
∴∠BDP=∠BNA=90°,
∵∠B=∠B,
∴△BDP∽△BNA,
∴,
∴,
解得t,
∴当t时,线段DP与⊙Q相切;
(2)
①出发后到DP与圆相切时,⊙Q与线段DP只有一个公共点,
∴0<t,
②当点P与点E重合后,点P在⊙Q内,此时⊙Q与线段DP只有一个公共点,
∵点P与点E重合时,
∵∠BED=∠ANB=90°,
∴DEAN,
∵,
∴BE=BP=,
∵BP+CP=BC,
∴,
解得:t,
∵当P到点B时,t==8,
∴t<8,
∴t<8,
综上,当0<t或时,⊙Q与线段DP只有一个公共点;
(3)
①当AP=CP时,由题意得:CP=2tcm,
过点A作AN⊥BC于点N,过点P作PM⊥AC于点M,如图2,
∵AB=AC=10cm,BC=16cm,AN⊥BC,
∴BN=NC,
∵AP=CP,PM⊥AC,
∴CM,
∵∠CMP=∠CNA=90°,∠C=∠C,
∴△CMP∽△CNA,
∴,
∴,
∴t;
②当AC=CP时,如图3,
则2t=10,
∴t=5;
③当点P到达点B时,此时CP=CB,
∴2t=16,
∴t=8,
综上,当△APC是等腰三角形时t的值为或5或8.
本题是圆的综合题,主要考查了动点问题,直线与圆的位置关系,相似三角形的判定与性质,等腰三角形的性质等知识,运用分类讨论思想是解题的关键.
20.(1)见解析;(2)或,点H运动路径的长为或;(3)
【解析】(1)先证,得到,根据AP是⊙O的切线,得到,继而得到,即可证明BH是⊙O的切线;
(2)过点B作⊙O的切线BC、BD,切点分别为C、D,连接OC,OD,可得到,继而得到,同理可得到,
当点H与点C重合时,可知,继而可求得,当点H与点D重合时,,继而可求得;
(3)作ON⊥AB于点N,则,因为h在圆上,所以,,则时△AHB面积最大.
(1)证明:,
,
又,
,
,
是⊙O的切线,
,
,即于点H,
是⊙O的切线;
(2)如图,过点B作⊙O的切线BC、BD,切点分别为C、D,连接OC,OD,则有,
,
,
,
同理,
当点H与点C重合时,由(1)知:,
,
,
的长为;
当点H与点D重合时,,
的长为,
当与⊙O相切时,旋转角或,点H运动路径的长为或.
(3)如图,作ON⊥AB于点N,
,其中表示H到直线AB的距离,
∵∠AOB=90°,OA=OB=4,
∴,
∴,
∴,
∵H在⊙O上,
∴,,
∴当时,最大,
∴当△AHB面积最大时,H到AB的距离为.
本题考查圆的切线、全等三角形的判定与性质、弧长公式、三角形的面积、勾股定理等,解题的关键是综合运用相关知识.
21.(1)6
(2)4π
【解析】(1)根据正六边形的边长与半径相等即可解决问题;
(2)由正六边形的性质和弧长公式即可得出结果.
(1)
解:∵六边形ABCDEF是正六边形,
∴正六边形的边长=半径OA=6;
(2)
∵六边形ABCDEF是正六边形,
∴∠BCF=120°,
∴弧BF的长为.
本题考查了正多边形和圆、弧长公式;熟练掌握正六边形的性质是解题的关键.
22.(1)2;相切
(2)
(3)
【解析】(1)根据勾股定理求出AC, 当点在上时,AC为⊙P的直径,可求出AP,再根据PC⊥CD,得出与的位置关系;
(2)根据切线的性质得到PE⊥BC,根据勾股定理列出方程,解方程求出AP;
(3) 当C在圆上时,与的边有公共点,且此时最小,当D在圆上时,与的边有公共点,且此时最大,以此求出两种情况下AP的取值范围即可.
(1)
解:∵四边形ABCD为平行四边形,
∴ABCD,BC=AD=5,
∵AB⊥AC,
∴∠ACD=∠BAC=90°,
∴AC==4,
当点在上时,AC为⊙P的直径,
∴⊙P的半径为2;
即AP=2
此时C在圆上,PC⊥CD,
故边CD与相切;
(2)
如图1,当⊙P与边BC相切时,设切点为E,连接PE,
则PE⊥BC,
∵AB⊥AC,点P在边AC上,
∴⊙P与AB相切.
∵⊙P与BC相切于点E,
∴BE=AB=3,EC=2,
设AP=x,则PE=x,PC=4 x,
在Rt△PCE中,由勾股定理得+4=,
解得x=,即AP=;
(3)
当C在圆上时,与的边有公共点,且此时最小,
即AP=2
当D在圆上时,如图2,与的边有公共点,且此时最大,
设PC=x,则PD=AP=4-x,CD=3
在Rt△CDP中,,
解得x=,4-x=,
即AP=,
综上所述:当时,与的边有公共点
本题考查的是直线与圆的位置关系、勾股定理、平行四边形的性质,掌握切线的性质定理是解题的关键.
23.(1)
(2)
【解析】(1)利用圆周角定理求出,然后由弧长公式可得出答案;
(2)由等腰三角形的性质求出,证明为等边三角形,由等边三角形的性质得出,由切线的性质求出,则可得出答案.
(1)
解:如图,连接,
∵,
∴,
∵过点,,的弧的半径为,
∴,
∴的长为,
∴的长为.
(2)
如图,连接,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵是的切线,
∴,
∴,
∴.
∴的度数为.
本题考查了弧长公式,圆周角定理,等边三角形的判定与性质,等腰三角形的性质,平行线的性质,切线的性质,直角三角形两锐角互余.理解和掌握切线的性质是解题的关键.
24.(1)见解析
(2)
【解析】(1)连接OC,如图,由AC平分∠EAB得到∠EAC= ∠OAC,于是可判断OC∥AE,根据平行线的性质得OC⊥CD,然后根据切线的判定定理得到结论;
(2)先根据圆周角定理得到∠ACB=90°,再判断Rt△AEC∽Rt△ACB,然后利用相似比可计算出AB,从而得到⊙O的半径.
(1)
如下图,连OC
∵AE⊥CD
∴ ∠AEC=90°
又 ∵OA=OC
∴∠OAC=∠OCA
∵ AC平分∠EAB
∴∠EAC= ∠OAC
∵∠EAC= ∠OCA
∴ OC∥AE
∴OC⊥DE
∴DE为切线.
(2)
如图,连BC
∵AB为直径
∴ ∠ACB=90°
又∵∠AEC =90°
∴∠ACB=∠AEC
又∵∠EAC= ∠BAC
∴ △AEC∽△ACB
∴=
∴=
∴AB=
∴r=
本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.
25.(1)证明见解析
(2)OA=10,
【解析】(1)根据正方形性质及圆切线性质知∠OMN=90°=∠D=∠C,再利用同角的余角相等可证得∠DOM=∠CMN,即得证;
(2)设半径为r,在直角三角形ODM中利用勾股定理求出r的值,进而得到OD、DM、CM的长度,再利用得,代入求值即可.
(1)
证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠DOM+∠OMD=90.
∴MN是的切线,
∴∠OMN=90°,
∴∠OMD+∠CMN=90°,
∴∠DOM=∠CMN,
∴.
(2)
解:设的半径为r,则OA=OM=r,OD=16﹣r.
在Rt△ODM中,根据勾股定理得:
,
即,
解得:r=10,
∴OA=10,
∴OD=16﹣10=6.
∵CD=16,DM=8,
∴CM=8.
∵,
∴,
即,
∴.
本题考查了圆的切线性质、相似三角形的判定及性质、勾股定理等知识点,掌握相似三角形的对应边成比例是解题关键.
26.(1)秒,4秒
(2)2
(3)存在,或
【解析】对于(1),根据点Q的速度和BC即可求出时间,再表示出点P的速度,根据路程相等列出方程求出t即可;
对于(2),分别表示出BQ,BP,根据勾股定理列出方程,求出解即可;
对于(3),当圆P与直线AD两次相切时,列出方程,求出t的值,并判断是否成立;当圆P与BD相切时,根据锐角三角函数列出方程,求出t.
(1)
秒,4秒.
当点Q与点B重合时,(秒);
根据题意可知CQ=3t,BP=t,当点Q在边AB上追上点P时,得
t+8=3t,
解得t=4.
故答案为:秒,4秒.
(2)
依题意BQ=8-3t,
在Rt△BPQ中, ,
即:,
解得,.
当Q在BC边上时,
∴.
当Q在BC边上时,t=2时,PQ的长为cm;
(3)
存在. 或.
当点P在AB上,点Q在BC上时,圆P与直线AD相切时,
BQ=8-3t,BP=t,QP=AP=6-t,根据勾股定理,得
,
即,
解得.
∵,
∴;
当点P,Q在AB上,圆P与直线AD相切时,
,
解得t=2.
∵当Q在BC边上时,
∴不合题意舍去;
当点P,Q在AB上,圆P与直线BD相切时,
可知PE⊥BD,于点E.
则BP=t,BQ=3t-8,
∴PQ=t-(3t-8)=8-2t,
即PE=8-2t.
又,
即,
解得.
所以或.
这是一道动点的综合问题,考查了切线的性质,勾股定理,一元二次方程的应用,锐角三角函数等.注意分情况讨论.
一、单选题
1.(2022·河北邯郸·九年级期末)平面内有两点P,O,⊙O的半径为5,若,则点P与⊙O的位置关系是( )
A.圆内 B.圆上 C.圆外 D.圆上或圆外
2.(2022·河北邢台·九年级期末)已知⊙O的半径为3,平面内有一点到圆心O的距离为5,则此点可能是( )
A.P点 B.Q点 C.M点 D.N点
3.(2022·河北承德·九年级期末)在中,,,以A为圆心2.5为半径作圆.下列结论中正确的是( )
A.直线BC与圆O相切 B.直线BC与相离 C.点B在圆内 D.点C在圆上
4.(2022·河北唐山·九年级期末)内接于,过点A作直线EF,已知,根据弦AB的变化,两人分别探究直线EF与的位置关系:
甲:如图1,当弦AB过点O时,EF与相切;
乙:如图2,当弦AB不过点O时,EF也与相切;
下列判断正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.甲乙都对 D.甲乙都不对
5.(2022·河北沧州·九年级期末)如图,是的内切圆,点,是切点,则下列说法不正确的是( )
A. B. C.的外心在的外面 D.四边形没有外接圆
6.(2022·河北保定·九年级期末)如图,中,内切圆I和边、、分别相切于点、、,若,,则的度数是( )
A.55° B.60° C.65° D.70°
7.(2022·河北邢台·九年级期末)已知△ABC中,∠ACB=90°,CD、CE分别是△ABC中线和高线,则( )
A.D点是△ABC的内心 B.D点是△ABC的外心
C.E点是△ABC的内心 D.E点是△ABC的外心
8.(2022·河北石家庄·九年级期末)如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在△ABC的外部,判断下列叙述不正确的是( )
A.O是△AEB的外心,O不是△AED的外心
B.O是△BEC的外心,O不是△BCD的外心
C.O是△AEC的外心,O不是△BCD的外心
D.O是△ADB的外心,O不是△ADC的外心
9.(2022·河北承德·九年级期末)在下列命题中,正确的是( )
A.三点确定一个圆 B.圆的内接等边三角形只有一个
C.一个三角形有且只有一个外接圆 D.一个四边形一定有外接圆
10.(2022·河北保定·九年级期末)如图,有一个直径为的圆形纸片,若在该纸片上沿虚线剪一个最大正六边形纸片,则这个正六边形纸片的边心距是( )
A.1 B. C.2 D.4
二、填空题
11.(2022·河北承德·九年级期末)如图,在扇形CAB中,,垂足为D,是△ACD的内切圆,连接AE,BE.
(1)∠AEB的度数为______;
(2)若,,则的长为______.
12.(2022·河北保定·九年级期末)如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB∥CD,若OB=6 cm,OC=8 cm,则BE+CG的长等于_____________
13.(2022·河北唐山·九年级期末)如图,在半径为10cm和6cm的两个同心圆中,大圆的弦AB与小圆相切于点C,则弦AB的长为_______cm.
14.(2022·河北沧州·九年级期末)如图,点I是的内心,连接AI并延长交的外接圆于点D, 若,则______;若,则______;
15.(2022·河北廊坊·九年级期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,如果∠A=15°,弦CD=4,那么AB的长是______.
16.(2022·河北保定·九年级期末)如图,⊙O的半径为2,点O到直线l的距离为4,过l上任一点P作⊙O的切线,切点为Q;若以PQ为边作正方形PQRS,则正方形PQRS的面积最小值为_______.
三、解答题
17.(2022·河北沧州·九年级期末)如图1,已知,点在射线上,且.以点为圆心,为半径作,交直线于点,.
(1)当与只有两个交点时,的取值范围是________;
(2)当时,将射线绕点按顺时针方向旋转.
①当为多少时,射线与相切;
②如图2,射线与交于,两点,若,求阴影部分的面积.
18.(2022·河北唐山·九年级期末)如图,⊙O是Rt△ABC的外接圆,直径AB=4,直线EF经过点C,AD⊥EF于点D,∠ACD=∠B.
(1)求证:EF是⊙O的切线;
(2)若AD=1,求DC的长;
(3)在(2)的条件下,求图中阴影部分的面积.
19.(2022·河北石家庄·九年级期末)如图,△ABC中,AB=AC=10cm.BC=16cm,动点P从点C出发沿线段CB以2cm/s的速度向点B运动,同时动点Q从点B出发沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也停止运动,设运动时间为t(单位:s),以点Q为圆心,BQ长为半径的⊙Q与射线BA、线段BC分别交于点D,E,连接DP.
(1)当t为何值时,线段DP与⊙Q相切;
(2)若⊙Q与线段DP只有一个公共点,求t的取值范围;
(3)当△APC是等腰三角形时,直接写出t的值.
20.(2022·河北石家庄·九年级期末)如图,在中,,以点O为圆心、2为半径画圆,过点A作的切线,切点为P,连接.将绕点O按逆时针方向旋转到时,连接.设旋转角为.
(1)当时,求证:是的切线;
(2)当与相切时,求旋转角和点H运动路径的长;
(3)当面积最大时,请直接写出此时点H到的距离.
21.(2022·河北邢台·九年级期末)已知正六边形ABCDEF的中心为O,半径OA=6.
(1)求正六边形的边长;
(2)以A为圆心,AF为半径画弧BF,求.
22.(2022·河北承德·九年级期末)如图,,,,,点在对角线上运动,以为圆心,为半径作.
(1)当点在上时,______,此时与的位置关系是______;
(2)当与边相切时,求的长;
(3)直接写出与的边有公共点时的取值范围.
23.(2022·河北廊坊·九年级期末)如图,中,,,过点,,的弧的半径为,点在上.,切线交的延长线于点.
(1)求的长;
(2)求的度数.
24.(2022·河北保定·九年级期末)如图,为直径,点C在上,平分,,垂足为E.
(1)求证:为切线.
(2)若,,求的半径.
25.(2022·河北邢台·九年级期末)如图所示的四边形ABCD是边长为16的正方形,O是边AD上的一个动点,且8
(2)当DM=8时,求OA,CN的长.
26.(2022·河北承德·九年级期末)如图,在矩形ABCD中,,,点P从点B出发,沿BA边向终点A以每秒1cm的速度运动,同时点Q从点C出发沿C-B-A向终点A以每秒3cm的速度运动,Q追上P时停止运动,设运动时间为t秒.解答下列问题:
(1)当______时点Q与点B重合,当______时点Q追上点P;
(2)当Q在BC边上时,求t为何值时PQ的长为cm;
(3)作为P为圆心,PQ长为半径作,是否存在这样的t值,使正好与的一边(或边所在的直线)相切?若存在直接写出t的值,若不存在,请说明理由.
参考答案:
1.C
【解析】根据点到圆心的距离小于半径即可判断点P在⊙O的内部.
∵⊙O的半径为5,PO=6,
∴点P到圆心O的距离大于半径,
∴点P在⊙O的外部,
故选C.
本题考查了点与圆的位置关系,理解点与圆的位置关系是解题的关键.
2.D
【解析】根据点到圆心O的距离大于半径,可判定出点在圆外,即可得到答案.
∵平面内有一点到圆心O的距离为5,5>3.
∴该点在圆外,
∴点N符合要求.
故选:D.
本题考查了点与圆的位置关系,根据点到圆心距离与半径的大小关系可作出判断.
3.B
【解析】过A点作AH⊥BC于H,如图,利用等腰三角形的性质得到BH=CH=BC=4,则利用勾股定理可计算出AH=3,然后根据直线与圆的位置关系的判定方法对A选项和B选项进行判断;根据点与圆的位置关系对C选项和D选项进行判断.
解:过A点作AH⊥BC于H,如图,
∵AB=AC,
∴BH=CH=BC=4,
在Rt△ABH中,,
∵AH⊥BC,AH=3>2.5,
∴直线BC与⊙A相离,所以A选项不符合题意,B选项符合题意.
∵AB=5>2.5,
∴B点在⊙A外,所以C选项不符合题意;
∵AC=5>2.5,
∴C点在⊙A外,所以D选项不符合题意;
故选:B.
本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,若直线l和⊙O相交 d<r;直线l和⊙O相切 d=r;直线l和⊙O相离 d>r.也考查了点与圆的位置关系和等腰三角形的性质.
4.C
【解析】甲:根据直径推出,推出,根据切线判定推出即可;
乙:作直径,连接,推出,求出,根据切线的判定推出即可.
解:甲:是的直径,
,
,
,
,
,
是半径,
是的切线;
乙:作直径,连接,
即(在同圆或等圆中,同弧所对的圆周角相等),
,
,
是的直径,
,
,
,
,
是半径,
是的切线.
故选:C.
考查了切线的判定,圆周角定理,三角形的内角和定理等知识点,注意:经过半径的外端且垂直于半径的直线是圆的切线,直径所对的圆周角是直角,正确应用定理等知识是解决问题的关键.
5.D
【解析】根据切线的定理可判断A,作于,可证四边形为正方形,即可判断B;根据为钝角三角形即可判断C;根据四边形的对角即可判断D.
解: ,是切点,
根据切线定理可知,故选项A正确,不满足题意;
作交于,
是的内切圆,
为切点,,
为切点,
,
四边形为正方形,
,故选项B正确,不满足题意;
由题可知为钝角三角形,
的外心在的外面,故选项C正确,不满足题意;
,
,
,
四边形有外接圆,故选项D错误,满足题意.
故选:D.
本题主要考查切线的性质,正方形的判定与性质,三角形的外心,四边形的外接圆,掌握相关定理与概念是解题的关键.
6.C
【解析】连接IE、IF,如图,根据切线的性质得到,利用四边形的内角和得到,再利用圆周角定理得到,然后根据三角形内角和求出,从而可计算出.
连接IE、IF,如图,
∵内切圆I和边AC、AB分别相切于点E、F,
∴,,
∴,
∵,
∴,
∵,,
∴,
∴,
故选:C.
本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆;三角形的内心与三角形顶点的连线平分这个内角.也考查了切线的性质.解题关键是根据三角形的内切圆与内心的性质作出合适的辅助线.
7.B
【解析】根据直角三角形斜边上的中线等于斜边的一半,可得是△ABC的外心,据此即可求解.
解:在△ABC中,∠ACB=90°,
∵CD是△ABC中线,
∴D点是△ABC的外心.
故选:B.
本题考查了三角形的外心,直角三角形斜边上的中线等于斜边的一半,掌握以上知识是解题的关键.
8.C
【解析】根据三角形的外心得出OA=OC=OB,根据正方形的性质得出OA=OC<OD,求出OA=OB=OC=OE≠OD,再逐个判断即可
连接OB、OD、OA,
∵O为锐角三角形ABC的外心,
∴OA=OC=OB,
∵四边形OCDE为正方形,
∴OA=OC<OD,
∴OA=OB=OC=OE≠OD,
∴OA=OE≠OD,即O不是△AED的外心,
OA=OE=OB,即O是△AEB的外心,
OA=OC=OE,即O是△ACE的外心,
OB=OA≠OD,即O不是△ABD的外心,
故选C.
本题考查了正方形的性质和三角形的外心与外接圆,能熟记知识点的内容是解此题的关键,注意:三角形的外心到三个顶点的距离相等,正方形的四边都相等.
9.C
【解析】利用确定圆的条件、圆内接三角形的定义、三角形外接圆的定义,四边形外接圆的定义分别判断后即可确定正确的选项.
解:A、不在同一直线上的三点确定一个圆,故错误;
B、圆内接等边三角形有无数个,故错误;
C、一个三角形有且只有一个外接圆,正确;
D、并不是所有的四边形都有外接圆,故错误,
故选:C.
本题考查了确定圆的条件、圆内接三角形的定义、三角形外接圆的定义,四边形外接圆的定义等知识,难度不大.
10.B
【解析】连接OA、OB,根据圆内接正六边形的性质得到△AOB是等边三角形,作OC⊥AB于C,求得∠AOC= 30°,由OA=2cm,得到AC=1cm,根据勾股定理求出OC即可.
如图,连接OA、OB,则△AOB是等边三角形,作OC⊥AB于C,
∵△AOB是等边三角形,
∴∠OAB= 60°,
∴∠AOC= 30°,
∵OA=2cm,
∴AC=1cm,
OC=,
故选:B.
此题考查圆内接正六边形的性质,等边三角形的性质,勾股定理,直角三角形30度角所对的直角边等于斜边的一半的性质,熟记圆内接正六边形的性质是解题的关键.
11. 135°
【解析】(1)如图,连接EC.首先证明∠AEC=135°,再证明△EAC≌△EAB即可解决问题;
(2)先利用已知求得∠CAB的度数,然后在直角三角形ACD中求得AC的长,最后利用弧长公即可求解.
解:(1)如图,连接EC.
∵E是△ADC的内心,∠ADC=90°,
∴∠ACE=∠ACD,∠EAC=∠CAD,
∴∠AEC=180° (∠ACD+∠CAD)=135°,
在△AEC和△AEB中,
,
∴△EAC≌△EAB,
∴∠AEB=∠AEC=135°,
故答案为135°.
(2)∵,∠AEB=135°,
∴ ,
∴,
∵,,
∴中,,
解得,
∴,
故答案为:
本题考查三角形的内心、全等三角形的判定和性质,弧长公式等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
12.10cm##10厘米
【解析】根据平行线的性质以及切线长定理,即可证明∠BOC=90°,再根据勾股定理即可求得BC的长,再结合切线长定理即可求解.
解:∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵直线AB,BC,CD分别与⊙O相切于E,F,G,
∴∠OBC=∠ABC,∠OCB=∠BCD,BE=BF,CG=CF,
∴∠OBC+∠OCB=(∠ABC+∠BCD)=90°,
∴∠BOC=90°,
在Rt△BOC中,
BC==10,
∴BE+CG=10(cm).
故答案为:10cm.
此题主要是考查了切线长定理.熟记从圆外一点引圆的两条切线,它们的切线长相等,且圆心和这点的连线平分两条切线的夹角是解决问题的关键.
13.16
【解析】根据切线的性质得到OC⊥AB,根据垂径定理得到AC=AB,根据勾股定理计算,得到答案.
解:∵AB是小圆O的切线,
∴OC⊥AB,
∵AB是大圆O的弦,
∴AC=AB,
在Rt△AOC中,AC===8(cm),
则AB=2AC=16(cm),
故答案为:16.
本题考查的是切线的性质、垂径定理和勾股定理的应用,掌握圆的切线垂直于经过切点的半径是解题的关键.
14. 125°
【解析】根据三角形内心的性质可得进而求得,再根据三角形内角和定理即可得到答案;
先求出,再根据外角的性质即可得到,再由三角形的内角和定理得出的度数即可.
点I是的内心
在中,
故答案为:125°;
点I是的内心
在中,
故答案为:.
本题考查了三角形外接圆与三角形的内心的性质、三角形的内角和定理、外角的性质,同弧所对的圆周角相等这些知识点,熟练掌握并能够运用是解题的关键.
15.8
【解析】首先根据圆的性质得出∠COB=30°,然后根据垂径定理得出CE=2,∠OEC=90°,解直角三角形得出OC,进而得出AB.
∵∠A=15°,
∴∠COB=30°,
∵AB是⊙O的直径,弦CD⊥AB于点E,弦CD=4,
∴CE=2,∠OEC=90°
∵∠COE=30°,
∴OC=2CE=4,
∴AB=2OC=8,
故答案为:8.
此题主要考查垂径定理以及含30°角直角三角形的性质,熟练掌握,即可解题.
16.12
【解析】连接OQ、OP,如图,根据切线的性质得OQ⊥PQ,则利用勾股定理得到PQ2=OP2﹣OQ2=OP2﹣4,也是判断OP取最小值时,PQ2的值最小,此时正方形PQRS的面积有最小值,根据垂线段最短得到OP的最小值为4,于是得到PQ2的最小值,从而确定正方形PQRS的面积的最小值.
解:连接OQ、OP,如图,
∵PQ为切线,
∴OQ⊥PQ,
在Rt△OPQ中,PQ2=OP2﹣OQ2=OP2﹣4,
当OP取最小值时,PQ2的值最小,此时正方形PQRS的面积有最小值,
而当OP⊥l时,OP取最小值,
∴OP的最小值为4,
∴PQ2的最小值为16﹣4=12,
∴正方形PQRS的面积最小值为12.
故答案为12.
本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.充分利用垂线段最短解决最小值问题.
17.(1))0<r<2或r>4
(2)①当α为15°或105°时,射线BA与⊙O相切;②S阴影=2π-4
【解析】(1)画出图形分: 当时,当时,时,时,时,五种情况讨论,即可得出答案;
(2)①分当射线BA在射线BC的上方与⊙O相切时和当射线BA在射线BC的下方与⊙O相切时,进行求解即可得出答案;
② 如图3,连接OM,ON,过点O作OQ⊥MN于点Q,由垂径定理可得出MQ=NQ=MN=,即可推得:∠MOQ=,故圆心角,由即可得出答案.
(1)
若与相切时,设切点为F,连接,如图:
则,
在中,,,
∴,
∴,
当时,与刚好有个交点,
∴当时, 如图:与只有两个交点;
当,即时,如图,与有个交点;
当即时,如图与有个交点;
当即时,如图,与有两个交点;
综上所述,当与只有两个交点时,的取值范围是或,
故答案为:或;
(2)
①如图1,当射线BA在射线BC的上方与⊙O相切时,设切点为P,连接OP.
∵OB=,OP=,
∴sinB==,
∴,
.
如图2,当射线BA在射线BC的下方与⊙O相切时,设切点为P,连接OP,
∵OB=,OP=,
∴sinB==,
∴,
∴.
综上所述,当α为或时,射线BA与⊙O相切;
②如图3,连接OM,ON,过点O作OQ⊥MN于点Q,
∴MQ=NQ=MN=.
∵OM=,
∴,
∴,
∴,
∴.
本题考查了直线与圆的位置关系,勾股定理,锐角三角函数、求弓形面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用特殊位置解决问题.
18.(1)见解析
(2)
(3)
【解析】(1)连接OC,由OB=OC,利用等边对等角得到∠BCO=∠B,由∠ACD=∠B,得到∠ACD+∠OCA=90°,得到OC垂直于EF,即可得到EF为圆O的切线;
(2)证明Rt△ABC∽Rt△ACD,可求出AC=2,由勾股定理求出CD的长即可;
(3)先证明△OAC为等边三角形,求出∠AOC=60°,即可由S阴影=S梯形ADCO-S扇形OAC求出答案.
(1)证明:连接OC,∵AB为⊙O直径,∴∠ACB=90°,∴∠B+∠BAC=90°∵OC=OA,∴∠OCA=∠OAC∵∠ACD=∠B,∴∠OCD=∠OCA+∠ACD=90°,即EF⊥OC∴EF是⊙O的切线
(2)解:∵AB是⊙O直径,∴∠ACB==90°,∵AD⊥EF于点D,∴∠∠ADC=90°,∴∠ADC=∠BCA,∵∠ACD=∠B,∴△ACD∽△ABC∴,∵AD=1,AB=4∴,∴AC=2∴
(3)解:∵AB=4,∴OC=OA=AB=2,由(2)知:AC=2,∴OC=OA=AC=2,∴△ACO为等边三角形,∴∠AOC=60°,由(2)知:CD=,AD=1∴S阴影=S梯形ADCO-S扇形OAC==.
本题是圆的综合题,考查了切线的判定,等腰三角形的性质,圆周角定理,相似三角形的判定与性质,等边三角形的判定与性质,勾股定理以及扇形面积的计算,熟练掌握圆的基础知识是解本题的关键.
19.(1)当t时,线段DP与⊙Q相切;
(2)0<t或;
(3)或5或8.
【解析】(1)过点A作AN⊥BC于点N,则BNcm,由线段DP与⊙Q相切,则∠BDP=∠BNA=90°,利用△BDP∽△BNA,得,代入即可求出t的值;
(2)分两种情形:出发后到DP与圆相切时,⊙Q与线段DP只有一个公共点,得0<t,当点P与点E重合后,点P在⊙Q内,此时⊙Q与线段DP只有一个公共点,当点P与点E重合时,,可解决问题;
(3)分AP=AC,PPC,CA=CP三种情形,分别画出图形,即可解决问题.
(1)
解:由题意得:CP=2tcm,BD=2tcm,则BP=(16﹣2t)cm,
过点A作AN⊥BC于点N,如图1,
则BNcm,
∵线段DP与⊙Q相切,
∴PD⊥BD,
∴∠BDP=∠BNA=90°,
∵∠B=∠B,
∴△BDP∽△BNA,
∴,
∴,
解得t,
∴当t时,线段DP与⊙Q相切;
(2)
①出发后到DP与圆相切时,⊙Q与线段DP只有一个公共点,
∴0<t,
②当点P与点E重合后,点P在⊙Q内,此时⊙Q与线段DP只有一个公共点,
∵点P与点E重合时,
∵∠BED=∠ANB=90°,
∴DEAN,
∵,
∴BE=BP=,
∵BP+CP=BC,
∴,
解得:t,
∵当P到点B时,t==8,
∴t<8,
∴t<8,
综上,当0<t或时,⊙Q与线段DP只有一个公共点;
(3)
①当AP=CP时,由题意得:CP=2tcm,
过点A作AN⊥BC于点N,过点P作PM⊥AC于点M,如图2,
∵AB=AC=10cm,BC=16cm,AN⊥BC,
∴BN=NC,
∵AP=CP,PM⊥AC,
∴CM,
∵∠CMP=∠CNA=90°,∠C=∠C,
∴△CMP∽△CNA,
∴,
∴,
∴t;
②当AC=CP时,如图3,
则2t=10,
∴t=5;
③当点P到达点B时,此时CP=CB,
∴2t=16,
∴t=8,
综上,当△APC是等腰三角形时t的值为或5或8.
本题是圆的综合题,主要考查了动点问题,直线与圆的位置关系,相似三角形的判定与性质,等腰三角形的性质等知识,运用分类讨论思想是解题的关键.
20.(1)见解析;(2)或,点H运动路径的长为或;(3)
【解析】(1)先证,得到,根据AP是⊙O的切线,得到,继而得到,即可证明BH是⊙O的切线;
(2)过点B作⊙O的切线BC、BD,切点分别为C、D,连接OC,OD,可得到,继而得到,同理可得到,
当点H与点C重合时,可知,继而可求得,当点H与点D重合时,,继而可求得;
(3)作ON⊥AB于点N,则,因为h在圆上,所以,,则时△AHB面积最大.
(1)证明:,
,
又,
,
,
是⊙O的切线,
,
,即于点H,
是⊙O的切线;
(2)如图,过点B作⊙O的切线BC、BD,切点分别为C、D,连接OC,OD,则有,
,
,
,
同理,
当点H与点C重合时,由(1)知:,
,
,
的长为;
当点H与点D重合时,,
的长为,
当与⊙O相切时,旋转角或,点H运动路径的长为或.
(3)如图,作ON⊥AB于点N,
,其中表示H到直线AB的距离,
∵∠AOB=90°,OA=OB=4,
∴,
∴,
∴,
∵H在⊙O上,
∴,,
∴当时,最大,
∴当△AHB面积最大时,H到AB的距离为.
本题考查圆的切线、全等三角形的判定与性质、弧长公式、三角形的面积、勾股定理等,解题的关键是综合运用相关知识.
21.(1)6
(2)4π
【解析】(1)根据正六边形的边长与半径相等即可解决问题;
(2)由正六边形的性质和弧长公式即可得出结果.
(1)
解:∵六边形ABCDEF是正六边形,
∴正六边形的边长=半径OA=6;
(2)
∵六边形ABCDEF是正六边形,
∴∠BCF=120°,
∴弧BF的长为.
本题考查了正多边形和圆、弧长公式;熟练掌握正六边形的性质是解题的关键.
22.(1)2;相切
(2)
(3)
【解析】(1)根据勾股定理求出AC, 当点在上时,AC为⊙P的直径,可求出AP,再根据PC⊥CD,得出与的位置关系;
(2)根据切线的性质得到PE⊥BC,根据勾股定理列出方程,解方程求出AP;
(3) 当C在圆上时,与的边有公共点,且此时最小,当D在圆上时,与的边有公共点,且此时最大,以此求出两种情况下AP的取值范围即可.
(1)
解:∵四边形ABCD为平行四边形,
∴ABCD,BC=AD=5,
∵AB⊥AC,
∴∠ACD=∠BAC=90°,
∴AC==4,
当点在上时,AC为⊙P的直径,
∴⊙P的半径为2;
即AP=2
此时C在圆上,PC⊥CD,
故边CD与相切;
(2)
如图1,当⊙P与边BC相切时,设切点为E,连接PE,
则PE⊥BC,
∵AB⊥AC,点P在边AC上,
∴⊙P与AB相切.
∵⊙P与BC相切于点E,
∴BE=AB=3,EC=2,
设AP=x,则PE=x,PC=4 x,
在Rt△PCE中,由勾股定理得+4=,
解得x=,即AP=;
(3)
当C在圆上时,与的边有公共点,且此时最小,
即AP=2
当D在圆上时,如图2,与的边有公共点,且此时最大,
设PC=x,则PD=AP=4-x,CD=3
在Rt△CDP中,,
解得x=,4-x=,
即AP=,
综上所述:当时,与的边有公共点
本题考查的是直线与圆的位置关系、勾股定理、平行四边形的性质,掌握切线的性质定理是解题的关键.
23.(1)
(2)
【解析】(1)利用圆周角定理求出,然后由弧长公式可得出答案;
(2)由等腰三角形的性质求出,证明为等边三角形,由等边三角形的性质得出,由切线的性质求出,则可得出答案.
(1)
解:如图,连接,
∵,
∴,
∵过点,,的弧的半径为,
∴,
∴的长为,
∴的长为.
(2)
如图,连接,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴,
∵,
∴是等边三角形,
∴,
∵是的切线,
∴,
∴,
∴.
∴的度数为.
本题考查了弧长公式,圆周角定理,等边三角形的判定与性质,等腰三角形的性质,平行线的性质,切线的性质,直角三角形两锐角互余.理解和掌握切线的性质是解题的关键.
24.(1)见解析
(2)
【解析】(1)连接OC,如图,由AC平分∠EAB得到∠EAC= ∠OAC,于是可判断OC∥AE,根据平行线的性质得OC⊥CD,然后根据切线的判定定理得到结论;
(2)先根据圆周角定理得到∠ACB=90°,再判断Rt△AEC∽Rt△ACB,然后利用相似比可计算出AB,从而得到⊙O的半径.
(1)
如下图,连OC
∵AE⊥CD
∴ ∠AEC=90°
又 ∵OA=OC
∴∠OAC=∠OCA
∵ AC平分∠EAB
∴∠EAC= ∠OAC
∵∠EAC= ∠OCA
∴ OC∥AE
∴OC⊥DE
∴DE为切线.
(2)
如图,连BC
∵AB为直径
∴ ∠ACB=90°
又∵∠AEC =90°
∴∠ACB=∠AEC
又∵∠EAC= ∠BAC
∴ △AEC∽△ACB
∴=
∴=
∴AB=
∴r=
本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.
25.(1)证明见解析
(2)OA=10,
【解析】(1)根据正方形性质及圆切线性质知∠OMN=90°=∠D=∠C,再利用同角的余角相等可证得∠DOM=∠CMN,即得证;
(2)设半径为r,在直角三角形ODM中利用勾股定理求出r的值,进而得到OD、DM、CM的长度,再利用得,代入求值即可.
(1)
证明:∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠DOM+∠OMD=90.
∴MN是的切线,
∴∠OMN=90°,
∴∠OMD+∠CMN=90°,
∴∠DOM=∠CMN,
∴.
(2)
解:设的半径为r,则OA=OM=r,OD=16﹣r.
在Rt△ODM中,根据勾股定理得:
,
即,
解得:r=10,
∴OA=10,
∴OD=16﹣10=6.
∵CD=16,DM=8,
∴CM=8.
∵,
∴,
即,
∴.
本题考查了圆的切线性质、相似三角形的判定及性质、勾股定理等知识点,掌握相似三角形的对应边成比例是解题关键.
26.(1)秒,4秒
(2)2
(3)存在,或
【解析】对于(1),根据点Q的速度和BC即可求出时间,再表示出点P的速度,根据路程相等列出方程求出t即可;
对于(2),分别表示出BQ,BP,根据勾股定理列出方程,求出解即可;
对于(3),当圆P与直线AD两次相切时,列出方程,求出t的值,并判断是否成立;当圆P与BD相切时,根据锐角三角函数列出方程,求出t.
(1)
秒,4秒.
当点Q与点B重合时,(秒);
根据题意可知CQ=3t,BP=t,当点Q在边AB上追上点P时,得
t+8=3t,
解得t=4.
故答案为:秒,4秒.
(2)
依题意BQ=8-3t,
在Rt△BPQ中, ,
即:,
解得,.
当Q在BC边上时,
∴.
当Q在BC边上时,t=2时,PQ的长为cm;
(3)
存在. 或.
当点P在AB上,点Q在BC上时,圆P与直线AD相切时,
BQ=8-3t,BP=t,QP=AP=6-t,根据勾股定理,得
,
即,
解得.
∵,
∴;
当点P,Q在AB上,圆P与直线AD相切时,
,
解得t=2.
∵当Q在BC边上时,
∴不合题意舍去;
当点P,Q在AB上,圆P与直线BD相切时,
可知PE⊥BD,于点E.
则BP=t,BQ=3t-8,
∴PQ=t-(3t-8)=8-2t,
即PE=8-2t.
又,
即,
解得.
所以或.
这是一道动点的综合问题,考查了切线的性质,勾股定理,一元二次方程的应用,锐角三角函数等.注意分情况讨论.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
