苏教版(2019)高中数学必修第一册《函数的单调性---抽象函数、复合函数单调性》名师课件(共14张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册《函数的单调性---抽象函数、复合函数单调性》名师课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 10:59:54 | ||
图片预览






文档简介
(共14张PPT)
在证明函数的单调性时,我们还可以利用其等价式子:任取,那么
在上是增函数;
在上是减函数.
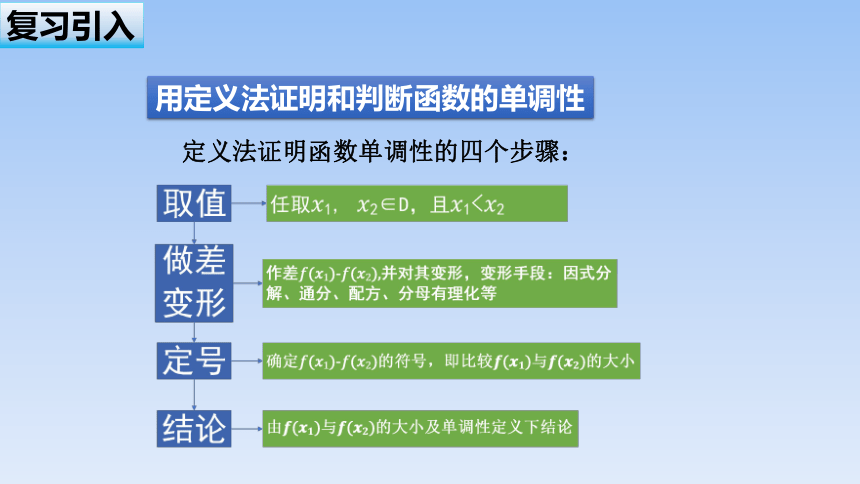
复习引入
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
复习引入
若函数在区间上具有单调性,则在区间上具有以下性质:
(1) 与( 为常数)具有相同的单调性.
(2)当时, 与具有相同的单调性;当时, 与具有相反的单调性.
(3)若恒为正值或恒为负值,则当时,与具有相反的单调性;当时,与具有相同的单调性.
(4)若0,则与具有相同的单调性.
(5)当都是增(减)函数时,若两者都恒大于零,则也是增(减)函数;若两者都恒小于零,则是减(增)函数.
复习引入
苏教版同步教材名师课件
函数的单调性
---抽象函数、复合函数单调性
复合函数的单调性
新知讲解
增函数 减函数 增函数 减函数
增函数 减函数 减函数 增函数
增函数 增函数 减函数 减函数
规律:
当两个函数的单调性相同时,其复合函数是增函数;
当两个函数的单调性不相同时,其复合函数是减函数.
复合函数的单调性可概括为一句话:“同增异减",注意先考虑定义域.
例1.已知函数,试判断此函数在上的单调性,并求出此函数在上的最大值和最小值.
思路分析
首先将复合函数分解成函数,然后只需判断在定义域上的单调性即可.
解析
函数可分解成函数
因为,所以,显然函数在上单调递增,函数在上单调递减,由复合函数的单调性,知上单调递减.
因此,函数在时取得最大值,最大值是2;在时取得最小值,最小值是0.4
典例讲解
典例讲解
例2.求的单调递增区间.
解析
的定义域为{|,或},令,则原函数可化为.
因为在上单调递减,在
上单调递增, 在其定义域内为增函数,
所以原函数在上单调递减,在上单调递增.
所以原函数的单调递增区间为.
方法归纳
(1)步骤:先求函数的定义域,接着分解复合函数,再判断每一层函数的单调性,最后根据复合函数的单调性确定函数的单调性
(2)若一个函数是由多个简单函数复合而成的,则此复合函数的单调性由简单函数中减函数的个数决定.若减函数有偶数个,则这个复合函数为增函数;若减函数有奇数个,则这个复合函数为减函数.
复合函数的单调性判断
变式训练
1.已知,求函数的单调区间.
解析
令,则从而,易知在上单调递减,在上单调递增.即的单调区间以1为界来划分.
令,得,易知的单调区间以0为界来划分.
由此可确定的单调性,如下表所示:
增 增 减 减
减 增 减 增
减 增 减 增
故的单调增区间是和,单调减区间是和.
抽象函数
新知讲解
抽象函数是指没有给出具体解析式的函数.
(1)合理赋值
根据函数的概念和性质,通过观察与分析,将一般量赋予特殊值,从而达到转化为要解决的问题的目的,这是常用的思维方式.
(2)凑配法
瞄准题设中的结构特点,采用加减添项或其他方法,以达到确定“”符号的目的.
(3)分拆变形
根据题目所给的关系进行分拆变形,构造出符合要求的结构形式.
解决抽象函数问题的常用方法
典例讲解
解析
∵ ∈ ,且,
∴.
例3.已知定义在上的函数对任意,恒有,且当时,判断在上的单调性.
设是区间上的任意两个实数,且,
∴
∴>0
∴,即
∴在上单调递减.
典例讲解
例4.已知函数对任意的,总有,且当时,求证:在上为减函数.
证明
在上任取设,则
∴
,
即,
∴在上为减函数.
∵当时,,∴ ,
方法归纳
若给出的是和型抽象函数,判定符号时的变形为
;
若给出的是积型抽象函数,判定符号时的变形为,
.
变式训练
2.已知函数对任意的,总有, ,且当时,
(1)求证: ;
(2)求证:恒有;
(3)求证: 是上的增函数;
证明
(3)在上任取设
∴在上为增函数.
(1)令: .∵,∴ .
(2)令: .
当时,当时,∴
∴当时,又 ,∴ 恒有.
由(2)知,又,>1,
故,
在证明函数的单调性时,我们还可以利用其等价式子:任取,那么
在上是增函数;
在上是减函数.
复习引入
用定义法证明和判断函数的单调性
定义法证明函数单调性的四个步骤:
复习引入
若函数在区间上具有单调性,则在区间上具有以下性质:
(1) 与( 为常数)具有相同的单调性.
(2)当时, 与具有相同的单调性;当时, 与具有相反的单调性.
(3)若恒为正值或恒为负值,则当时,与具有相反的单调性;当时,与具有相同的单调性.
(4)若0,则与具有相同的单调性.
(5)当都是增(减)函数时,若两者都恒大于零,则也是增(减)函数;若两者都恒小于零,则是减(增)函数.
复习引入
苏教版同步教材名师课件
函数的单调性
---抽象函数、复合函数单调性
复合函数的单调性
新知讲解
增函数 减函数 增函数 减函数
增函数 减函数 减函数 增函数
增函数 增函数 减函数 减函数
规律:
当两个函数的单调性相同时,其复合函数是增函数;
当两个函数的单调性不相同时,其复合函数是减函数.
复合函数的单调性可概括为一句话:“同增异减",注意先考虑定义域.
例1.已知函数,试判断此函数在上的单调性,并求出此函数在上的最大值和最小值.
思路分析
首先将复合函数分解成函数,然后只需判断在定义域上的单调性即可.
解析
函数可分解成函数
因为,所以,显然函数在上单调递增,函数在上单调递减,由复合函数的单调性,知上单调递减.
因此,函数在时取得最大值,最大值是2;在时取得最小值,最小值是0.4
典例讲解
典例讲解
例2.求的单调递增区间.
解析
的定义域为{|,或},令,则原函数可化为.
因为在上单调递减,在
上单调递增, 在其定义域内为增函数,
所以原函数在上单调递减,在上单调递增.
所以原函数的单调递增区间为.
方法归纳
(1)步骤:先求函数的定义域,接着分解复合函数,再判断每一层函数的单调性,最后根据复合函数的单调性确定函数的单调性
(2)若一个函数是由多个简单函数复合而成的,则此复合函数的单调性由简单函数中减函数的个数决定.若减函数有偶数个,则这个复合函数为增函数;若减函数有奇数个,则这个复合函数为减函数.
复合函数的单调性判断
变式训练
1.已知,求函数的单调区间.
解析
令,则从而,易知在上单调递减,在上单调递增.即的单调区间以1为界来划分.
令,得,易知的单调区间以0为界来划分.
由此可确定的单调性,如下表所示:
增 增 减 减
减 增 减 增
减 增 减 增
故的单调增区间是和,单调减区间是和.
抽象函数
新知讲解
抽象函数是指没有给出具体解析式的函数.
(1)合理赋值
根据函数的概念和性质,通过观察与分析,将一般量赋予特殊值,从而达到转化为要解决的问题的目的,这是常用的思维方式.
(2)凑配法
瞄准题设中的结构特点,采用加减添项或其他方法,以达到确定“”符号的目的.
(3)分拆变形
根据题目所给的关系进行分拆变形,构造出符合要求的结构形式.
解决抽象函数问题的常用方法
典例讲解
解析
∵ ∈ ,且,
∴.
例3.已知定义在上的函数对任意,恒有,且当时,判断在上的单调性.
设是区间上的任意两个实数,且,
∴
∴>0
∴,即
∴在上单调递减.
典例讲解
例4.已知函数对任意的,总有,且当时,求证:在上为减函数.
证明
在上任取设,则
∴
,
即,
∴在上为减函数.
∵当时,,∴ ,
方法归纳
若给出的是和型抽象函数,判定符号时的变形为
;
若给出的是积型抽象函数,判定符号时的变形为,
.
变式训练
2.已知函数对任意的,总有, ,且当时,
(1)求证: ;
(2)求证:恒有;
(3)求证: 是上的增函数;
证明
(3)在上任取设
∴在上为增函数.
(1)令: .∵,∴ .
(2)令: .
当时,当时,∴
∴当时,又 ,∴ 恒有.
由(2)知,又,>1,
故,
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
