苏州市第五中学2006~2007学年度第一学期期中高二数学试卷[上学期]
文档属性
| 名称 | 苏州市第五中学2006~2007学年度第一学期期中高二数学试卷[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-10 00:00:00 | ||
图片预览


文档简介
苏州市第五中学
2006~2007学年度第一学期期中试卷
高二数学
一、选择题(本大题共10小题,每小题5分,共50分)
1.某城市有学校700所,其中大学20所,中学200所,小学480所.现用分层抽样的方法从中抽取一个容量为70的样本进行某项调查,则应抽取的中学数为 ( B )
A.70 B.20 C.48 D.2
2.“”是“的 ( B )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
3.一家旅社有100间相同的客房,经过一段时间经营实践,发现有如下表给出的关系,为使每天总收入达到最高,每间客房每天的定价应为 ( C )
每间每天定价
70元
60元
50元
40元
住房率
55%
65%
80%
95%
A.70元 B.60元 C.50元 D.40元
4.根据如图所示的流程图计算,输出的结果是 ( C )
A.21 B.101 C.231 D.301
5.从一批产品中取出三件产品,记为事件“三件产品全不是次品”,为事件“三件产品全是次品”,
为“三件产品不全是次品”,则下列结论正确的是 ( B )
A.与互斥 B.与互斥
C.任何两个均互斥 D.任何两个均不互斥
6.如图所示的伪代码,最终输出的结果是 ( D )
A.的值 B.的值
C.的值 D.的值
7.是,,,的平均数,是,,,的平均数,是,,,的平均
数,则下列各式正确的是 ( A )
A. B. C. D.
8.如图,靶子由三个半径分别为的同心圆组成,如果某人向靶子随机地掷一
个飞镖(不偏离靶子,且等可能命中靶面上的任何点),命中区域Ⅰ,Ⅱ,Ⅲ的概率
分别为,则为 ( D )
A. B.
C. D.
9.从装有红球、黑球和白球的口袋中摸出1只球.若摸出的球是红球的概率是,摸出的球是黑球的概
率是,那么摸出的球是白球的概率是 ( A )
A. B. C. D.不能确定
10.在样本频率分布直方图中,共有11个小的长方形,若中间一个小长方形的面积等于其它10个小长方
形面积的和的,且样本容量为160,则中间一组的频数为 ( A )
A.32 B.0.2 C.40 D.0.25
二、填空题(本大题共6小题,每小题5分,共30分)
11.将容量为100的样本数据分为如下8组:
则第3组的频率为.
12.下列算法中,最后输出的分别是 -5 , 6 , 6 .
13.通过对有关数据的分析可知,每立方米混凝土的水泥用量(单位:)与28天后混凝土的抗压强度
(单位:)之间具有线性相关关系,其线性回归方程为. 根据某个建设项目的须要,28天后混凝土的抗压强度不得低于,问每立方米混凝土的水泥用量最少应为 266 (精确到个位).
14.在共4个数字中,任取两个数字(允许重复),其中一个数字是另一个数字的2倍的概率是.
15.在集合内,任取1个元素,使不等式式成立的概率是.
16.对任意实数,在下列命题中,真命题是 ② .
①“”是“”的必要条件;②“”是“”的必要条件;
③“”是“”的充分条件;④“”是“”的充分条件.
三、解答题(本大题共5小题,共70分)
17.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(Ⅰ)3个小矩形颜色都相同的概率;
(Ⅱ)3个小矩形颜色都不同的概率.
【解答】画树形图(图略)可知,本题的基本事件共有27个.
(Ⅰ)记“3个矩形都涂同一颜色”为事件,事件的基本事件有3个,故
.
(Ⅱ)记“3个矩形颜色都不同”为事件,事件的基本事件有6个,故
.
【答】3个小矩形颜色都相同的概率为,3个小矩形颜色都不同的概率为.
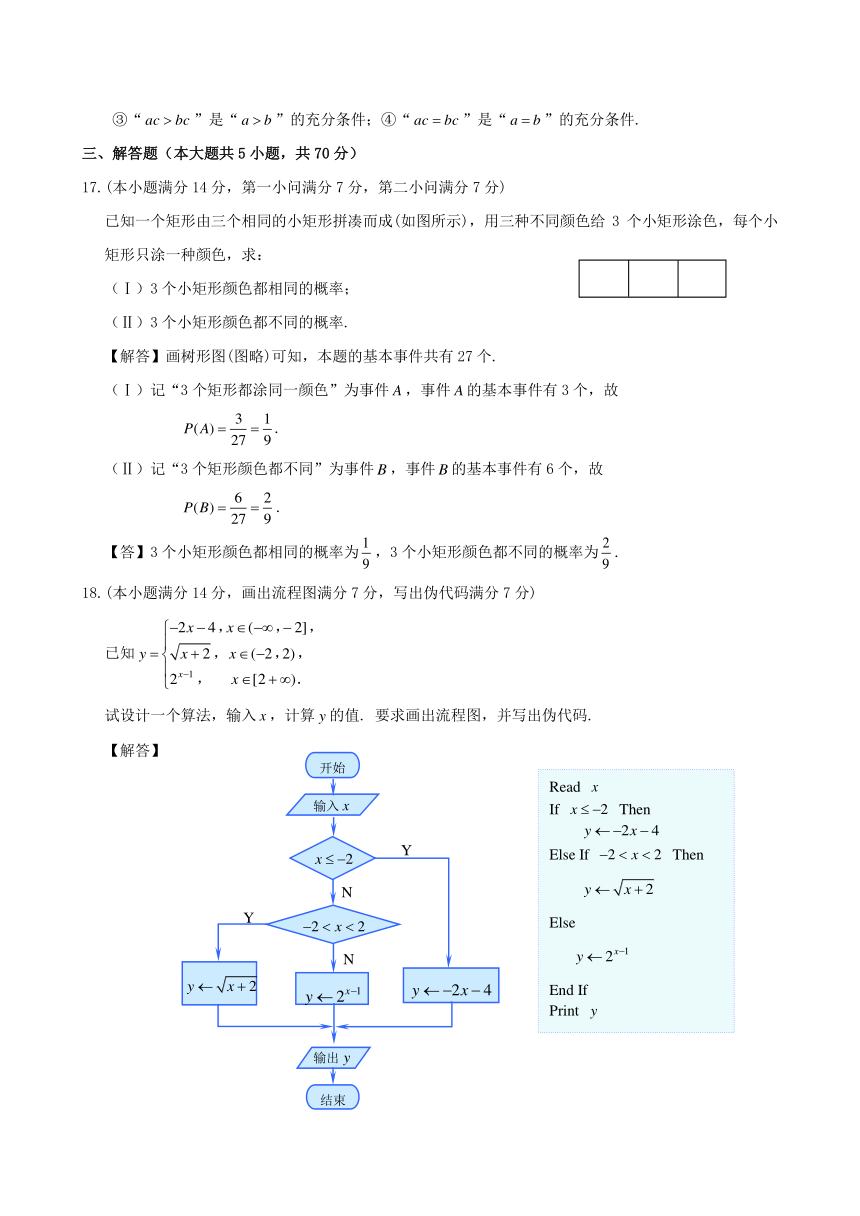
18.(本小题满分14分,画出流程图满分7分,写出伪代码满分7分)
已知
试设计一个算法,输入,计算的值. 要求画出流程图,并写出伪代码.
【解答】
19.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
下面是从某校高一学生中抽取的20名学生的学习用书的重量(单位:):
8.4 10.1 6.3 7.1 6.2 6.5 7.6 8.0 8.5 6.4
10.3 8.5 5.2 4.6 7.8 3.9 4.8 7.2 8.0 6.8
(Ⅰ)列出频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)利用频率分布直方图的组中值对总体平均数及方差进行估计.
解题要求:在将数据进行分组时,取区间端点为整数,组距为1. 否则,不给分.
【解答】(Ⅰ)这20个数的最小值为3.9,最大值为10.3,相差6.4,以1为组距,将数据分为8组,列出频率分布表如下:
分 组
频 数
频 率
1
0.05
2
0.1
1
0.05
5
0.25
4
0.2
5
0.25
0
0
2
0.1
合计
20
1
(Ⅱ)
(Ⅲ)用组中值估计:
平均数
().
方差
().
20.(本小题满分16分,每小问满分均为4分)
将完全相同的3个球随机地放入号盒子中(每盒放球数不限),求:
(Ⅰ)3个球放入同一个盒子的概率;
(Ⅱ)3个盒子中都有球的概率;
(Ⅲ)至少有一个盒子没球的概率;
(Ⅳ)恰有一个盒子没有球的概率.
【解答】利用树形图可知,将完全相同的3个球随机地放入号盒子中,共有种放法,每种放法是等可能的.
(Ⅰ)记“3个球放入同一个盒子的概率”为事件.
3个球放入同一个盒子的放法有3种:3个球放入1号盒子,或2号盒子,或3号盒子.
故.
(Ⅱ)记“3个球放入3个盒子,每个盒子中都有球”为事件.
3个球放入3个盒子,每个盒子中都有球,等价于每个盒子只放1个球,有6种方法.
故.
(Ⅲ)记“3个球放入3个盒子,至少有一个盒子没球”为事件.
因为事件C是事件B的对立事件,所以.
(Ⅳ)记“3个球放入3个盒子,恰有一个盒子没有球”为事件.
由题意可知,.
因为事件和是互斥事件,所以,.
21.(本小题满分12分,第一小问满分4分,第二小问满分8分)
将曲线,,和所围成的平面区域记作,将直线,,和
所围成的正方形区域记作.
(Ⅰ)在直角坐标平面上,作出区域和;
(Ⅱ)利用随机模拟方法,我们可以估算区域的面积,也就是说,在区域内随机产生个点,数出落在区域内点的个数,用几何概型公式计算区域的面积. 请按此思路,设计一个算法,估算区域的面积,只要求写出伪代码.
提示:若点,则当时,.
【解答】(Ⅰ) (Ⅱ)
2006~2007学年度第一学期期中试卷
高二数学
一、选择题(本大题共10小题,每小题5分,共50分)
1.某城市有学校700所,其中大学20所,中学200所,小学480所.现用分层抽样的方法从中抽取一个容量为70的样本进行某项调查,则应抽取的中学数为 ( B )
A.70 B.20 C.48 D.2
2.“”是“的 ( B )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
3.一家旅社有100间相同的客房,经过一段时间经营实践,发现有如下表给出的关系,为使每天总收入达到最高,每间客房每天的定价应为 ( C )
每间每天定价
70元
60元
50元
40元
住房率
55%
65%
80%
95%
A.70元 B.60元 C.50元 D.40元
4.根据如图所示的流程图计算,输出的结果是 ( C )
A.21 B.101 C.231 D.301
5.从一批产品中取出三件产品,记为事件“三件产品全不是次品”,为事件“三件产品全是次品”,
为“三件产品不全是次品”,则下列结论正确的是 ( B )
A.与互斥 B.与互斥
C.任何两个均互斥 D.任何两个均不互斥
6.如图所示的伪代码,最终输出的结果是 ( D )
A.的值 B.的值
C.的值 D.的值
7.是,,,的平均数,是,,,的平均数,是,,,的平均
数,则下列各式正确的是 ( A )
A. B. C. D.
8.如图,靶子由三个半径分别为的同心圆组成,如果某人向靶子随机地掷一
个飞镖(不偏离靶子,且等可能命中靶面上的任何点),命中区域Ⅰ,Ⅱ,Ⅲ的概率
分别为,则为 ( D )
A. B.
C. D.
9.从装有红球、黑球和白球的口袋中摸出1只球.若摸出的球是红球的概率是,摸出的球是黑球的概
率是,那么摸出的球是白球的概率是 ( A )
A. B. C. D.不能确定
10.在样本频率分布直方图中,共有11个小的长方形,若中间一个小长方形的面积等于其它10个小长方
形面积的和的,且样本容量为160,则中间一组的频数为 ( A )
A.32 B.0.2 C.40 D.0.25
二、填空题(本大题共6小题,每小题5分,共30分)
11.将容量为100的样本数据分为如下8组:
则第3组的频率为.
12.下列算法中,最后输出的分别是 -5 , 6 , 6 .
13.通过对有关数据的分析可知,每立方米混凝土的水泥用量(单位:)与28天后混凝土的抗压强度
(单位:)之间具有线性相关关系,其线性回归方程为. 根据某个建设项目的须要,28天后混凝土的抗压强度不得低于,问每立方米混凝土的水泥用量最少应为 266 (精确到个位).
14.在共4个数字中,任取两个数字(允许重复),其中一个数字是另一个数字的2倍的概率是.
15.在集合内,任取1个元素,使不等式式成立的概率是.
16.对任意实数,在下列命题中,真命题是 ② .
①“”是“”的必要条件;②“”是“”的必要条件;
③“”是“”的充分条件;④“”是“”的充分条件.
三、解答题(本大题共5小题,共70分)
17.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(Ⅰ)3个小矩形颜色都相同的概率;
(Ⅱ)3个小矩形颜色都不同的概率.
【解答】画树形图(图略)可知,本题的基本事件共有27个.
(Ⅰ)记“3个矩形都涂同一颜色”为事件,事件的基本事件有3个,故
.
(Ⅱ)记“3个矩形颜色都不同”为事件,事件的基本事件有6个,故
.
【答】3个小矩形颜色都相同的概率为,3个小矩形颜色都不同的概率为.
18.(本小题满分14分,画出流程图满分7分,写出伪代码满分7分)
已知
试设计一个算法,输入,计算的值. 要求画出流程图,并写出伪代码.
【解答】
19.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
下面是从某校高一学生中抽取的20名学生的学习用书的重量(单位:):
8.4 10.1 6.3 7.1 6.2 6.5 7.6 8.0 8.5 6.4
10.3 8.5 5.2 4.6 7.8 3.9 4.8 7.2 8.0 6.8
(Ⅰ)列出频率分布表;
(Ⅱ)画出频率分布直方图;
(Ⅲ)利用频率分布直方图的组中值对总体平均数及方差进行估计.
解题要求:在将数据进行分组时,取区间端点为整数,组距为1. 否则,不给分.
【解答】(Ⅰ)这20个数的最小值为3.9,最大值为10.3,相差6.4,以1为组距,将数据分为8组,列出频率分布表如下:
分 组
频 数
频 率
1
0.05
2
0.1
1
0.05
5
0.25
4
0.2
5
0.25
0
0
2
0.1
合计
20
1
(Ⅱ)
(Ⅲ)用组中值估计:
平均数
().
方差
().
20.(本小题满分16分,每小问满分均为4分)
将完全相同的3个球随机地放入号盒子中(每盒放球数不限),求:
(Ⅰ)3个球放入同一个盒子的概率;
(Ⅱ)3个盒子中都有球的概率;
(Ⅲ)至少有一个盒子没球的概率;
(Ⅳ)恰有一个盒子没有球的概率.
【解答】利用树形图可知,将完全相同的3个球随机地放入号盒子中,共有种放法,每种放法是等可能的.
(Ⅰ)记“3个球放入同一个盒子的概率”为事件.
3个球放入同一个盒子的放法有3种:3个球放入1号盒子,或2号盒子,或3号盒子.
故.
(Ⅱ)记“3个球放入3个盒子,每个盒子中都有球”为事件.
3个球放入3个盒子,每个盒子中都有球,等价于每个盒子只放1个球,有6种方法.
故.
(Ⅲ)记“3个球放入3个盒子,至少有一个盒子没球”为事件.
因为事件C是事件B的对立事件,所以.
(Ⅳ)记“3个球放入3个盒子,恰有一个盒子没有球”为事件.
由题意可知,.
因为事件和是互斥事件,所以,.
21.(本小题满分12分,第一小问满分4分,第二小问满分8分)
将曲线,,和所围成的平面区域记作,将直线,,和
所围成的正方形区域记作.
(Ⅰ)在直角坐标平面上,作出区域和;
(Ⅱ)利用随机模拟方法,我们可以估算区域的面积,也就是说,在区域内随机产生个点,数出落在区域内点的个数,用几何概型公式计算区域的面积. 请按此思路,设计一个算法,估算区域的面积,只要求写出伪代码.
提示:若点,则当时,.
【解答】(Ⅰ) (Ⅱ)
