江苏省栟茶高级中学高二年级第一学期期中考试-苏教版[上学期]
文档属性
| 名称 | 江苏省栟茶高级中学高二年级第一学期期中考试-苏教版[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 82.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-19 07:44:00 | ||
图片预览


文档简介
江苏省栟茶高级中学高二年级第一学期期中考试
数 学 试 题 2006.11
YCY命题
试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分200分,考试用时120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题:(本大题共10小题,每小题分,共50分,在每小题给出的四个选项中,仅有一项是符合题目要求的.)
1.某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,则老年人、,中年人、青年人分别各抽取的人数是( )
A.6, 12 ,18 B. 7,11,19 C.6,13,17 D. 7,12,17
2.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么对立的两个事件是 ( )
A、至少有1个白球,都是红球 B、至少有1个白球,至少有1个红球
C、恰有1个白球,恰有2个白球 D、至少有1个白球,都是白球
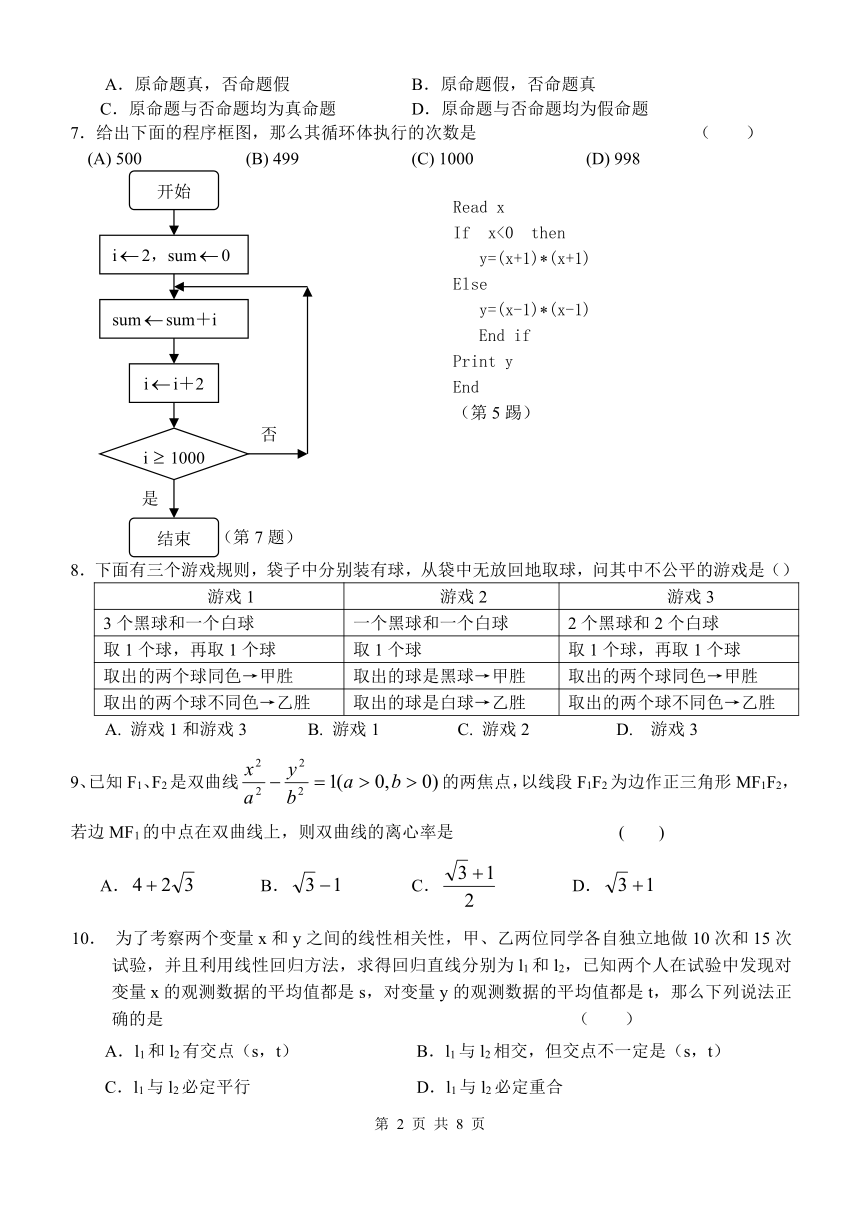
3、为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 ( )
A.20 B.30 C.40 D.50
4.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数为1.8,全年比赛进球个数的标准差为0.3.下列说法里:
①甲队的技术比乙队好 ②乙队发挥比甲队稳定
③乙队几乎每场都进球 ④甲队的表现时好时坏
其中,正确的个数为 ( )
A.1 B.2 C.3 D.4
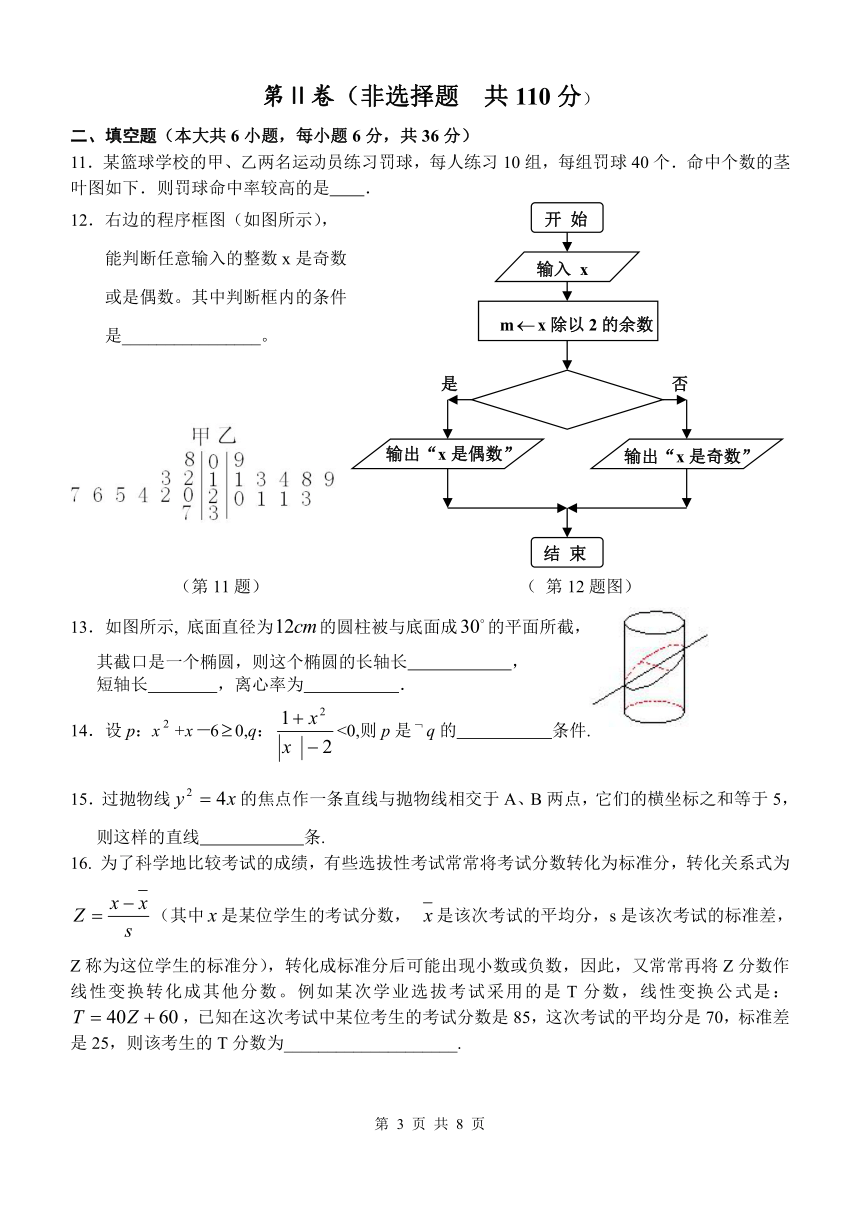
5.为了在运行下面的程序之后得到输出y=16,键盘输入x应该是(见第7题下)( )
(A) 3或-3 (B) -5 (C) -5或5 (D) 5或-3
6.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其否命题的真假情况是()
A.原命题真,否命题假 B.原命题假,否命题真
C.原命题与否命题均为真命题 D.原命题与否命题均为假命题
7.给出下面的程序框图,那么其循环体执行的次数是 ( )
(A) 500 (B) 499 (C) 1000 (D) 998
8.下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是()
游戏1
游戏2
游戏3
3个黑球和一个白球
一个黑球和一个白球
2个黑球和2个白球
取1个球,再取1个球
取1个球
取1个球,再取1个球
取出的两个球同色→甲胜
取出的球是黑球→甲胜
取出的两个球同色→甲胜
取出的两个球不同色→乙胜
取出的球是白球→乙胜
取出的两个球不同色→乙胜
A. 游戏1和游戏3 B. 游戏1 C. 游戏2 D. 游戏3
9、已知F1、F2是双曲线的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A. B. C. D.
10. 为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是 ( )
A.l1和l2有交点(s,t) B.l1与l2相交,但交点不一定是(s,t)
C.l1与l2必定平行 D.l1与l2必定重合
第Ⅱ卷(非选择题 共110分)
二、填空题(本大共6小题,每小题6分,共36分)
11.某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则罚球命中率较高的是 .
12.右边的程序框图(如图所示),
能判断任意输入的整数x是奇数
或是偶数。其中判断框内的条件
是________________。
(第11题) ( 第12题图)
13.如图所示, 底面直径为的圆柱被与底面成的平面所截,
其截口是一个椭圆,则这个椭圆的长轴长 ,
短轴长 ,离心率为 .
14.设p:x+x-60,q:<0,则p是q的 条件.
15.过抛物线的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线 条.
16. 为了科学地比较考试的成绩,有些选拔性考试常常将考试分数转化为标准分,转化关系式为(其中是某位学生的考试分数, 是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分),转化成标准分后可能出现小数或负数,因此,又常常再将Z分数作线性变换转化成其他分数。例如某次学业选拔考试采用的是T分数,线性变换公式是:,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为____________________.
江苏省南通中学高二期中考试数学答题纸
一、选择题答案(每题5分)
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题答案(每题6分)
11、 12、 13、
14、 15、 16、
三、解答题(本大题共6小题、共74分,解答给出文字说明,演算步骤)
17.(本小题满分14分,第一、二小问满分各7分)某热水瓶胆生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:(1)2件都是一级品的概率;(2)至少有一件二级品的概率.
18.(本小题满分15分,第一、二小问满分分别是7分、8分)
已知算法:(1)指出其功能(用算式表示),
(2)将该算法用流程图描述之。
19.(本小题满分14分,第一、二小问满分各7分)
设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
20.(本小题满分15分,第一、二小问满分分别是7、8分)
已知,根据下列条件求为钝角三角形的概率:
在线段OB上任取一点C;
过点A任作一直线与直线OB交于点C.
21.(本小题满分16分,第一、二小问满分各8分)
设A、B是椭圆上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(1)确定的取值范围,并求直线AB的方程;
(2)试判断是否存在这样的,使得A、B、C、D四点在同一个圆上?并说明理由.
高二年级第一学期期中考试答案
选择题
AACDC ABDDA
二、填空题
11.甲; 12.m=0 ; 13. ;
14.充分非必要; 15. 有且仅有两条; 16、84
三、解答题
17. 解: (1)设2件都是一级品为事件A.……………………………1分
从10件产品中抽取2件,共有45个基本事件,且都是等可能的3分
而事件A的结果(即包含的基本事件数)有28种, ……… …5分
则P(A)=. ………………………………………………7分
(2)设至少有一件二级品为事件B,……………………………………8分
则B是两个互斥事件:“抽取的2件产品中包含了一件一级品,一件二级品(记为B1)”与“抽取的2件产品均为二级品(B2)”的和. ………9分
而P(B1)=,P(B2)=, …………………10分
∴P(B)=P(B1+B2)= P(B1)+ P(B2) ……………11分
=. …………………………………13分
答: 2件都是一级品的概率为;至少有一件二级品的概率为.14分
18.解:算法的功能为:……………………………7分
程序框图为:
………………………………………………15分
19.解:(1)椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.又点A(1,)在椭圆上,因此=1得b2=3,于是c2=1.…4分
所以椭圆C的方程为=1,………5分
焦点F1(-1,0),F2(1,0). ……………7分
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:
, 即x1=2x+1,y1=2y.…………10分
因此=1.即为所求的轨迹方程. ……………14分
20. 解:(1); (2).
21. (1)依题意,可设直线AB的方程为,整理得 ①
设①的两个不同的根, ② …………4分
是线段AB的中点,得解得k=-1,代入②得,>12,即的取值范围是(12,+).……6分
于是,直线AB的方程为………8分
(2)代入椭圆方程,整理得 ③
③的两根,
于是由弦长公式可得 ④……10分
将直线AB的方程 ⑤
同理可得 ⑥
……12分
假设在>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.点M到直线AB的距离为 ⑦
于是,由④、⑥、⑦式和勾股定理可得
故当时,A、B、C、D四点均在以M为圆心,为半径的圆上.……16分
数 学 试 题 2006.11
YCY命题
试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分200分,考试用时120分钟.
第Ⅰ卷(选择题,共50分)
一、选择题:(本大题共10小题,每小题分,共50分,在每小题给出的四个选项中,仅有一项是符合题目要求的.)
1.某单位有老年人28 人,中年人54人,青年人81人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,则老年人、,中年人、青年人分别各抽取的人数是( )
A.6, 12 ,18 B. 7,11,19 C.6,13,17 D. 7,12,17
2.从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么对立的两个事件是 ( )
A、至少有1个白球,都是红球 B、至少有1个白球,至少有1个红球
C、恰有1个白球,恰有2个白球 D、至少有1个白球,都是白球
3、为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 ( )
A.20 B.30 C.40 D.50
4.甲、乙两支女子曲棍球队在去年的国际联赛中,甲队平均每场进球数为3.2,全年比赛进球个数的标准差为3;乙队平均每场进球数为1.8,全年比赛进球个数的标准差为0.3.下列说法里:
①甲队的技术比乙队好 ②乙队发挥比甲队稳定
③乙队几乎每场都进球 ④甲队的表现时好时坏
其中,正确的个数为 ( )
A.1 B.2 C.3 D.4
5.为了在运行下面的程序之后得到输出y=16,键盘输入x应该是(见第7题下)( )
(A) 3或-3 (B) -5 (C) -5或5 (D) 5或-3
6.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其否命题的真假情况是()
A.原命题真,否命题假 B.原命题假,否命题真
C.原命题与否命题均为真命题 D.原命题与否命题均为假命题
7.给出下面的程序框图,那么其循环体执行的次数是 ( )
(A) 500 (B) 499 (C) 1000 (D) 998
8.下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是()
游戏1
游戏2
游戏3
3个黑球和一个白球
一个黑球和一个白球
2个黑球和2个白球
取1个球,再取1个球
取1个球
取1个球,再取1个球
取出的两个球同色→甲胜
取出的球是黑球→甲胜
取出的两个球同色→甲胜
取出的两个球不同色→乙胜
取出的球是白球→乙胜
取出的两个球不同色→乙胜
A. 游戏1和游戏3 B. 游戏1 C. 游戏2 D. 游戏3
9、已知F1、F2是双曲线的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是 ( )
A. B. C. D.
10. 为了考察两个变量x和y之间的线性相关性,甲、乙两位同学各自独立地做10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2,已知两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,那么下列说法正确的是 ( )
A.l1和l2有交点(s,t) B.l1与l2相交,但交点不一定是(s,t)
C.l1与l2必定平行 D.l1与l2必定重合
第Ⅱ卷(非选择题 共110分)
二、填空题(本大共6小题,每小题6分,共36分)
11.某篮球学校的甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则罚球命中率较高的是 .
12.右边的程序框图(如图所示),
能判断任意输入的整数x是奇数
或是偶数。其中判断框内的条件
是________________。
(第11题) ( 第12题图)
13.如图所示, 底面直径为的圆柱被与底面成的平面所截,
其截口是一个椭圆,则这个椭圆的长轴长 ,
短轴长 ,离心率为 .
14.设p:x+x-60,q:<0,则p是q的 条件.
15.过抛物线的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于5,则这样的直线 条.
16. 为了科学地比较考试的成绩,有些选拔性考试常常将考试分数转化为标准分,转化关系式为(其中是某位学生的考试分数, 是该次考试的平均分,s是该次考试的标准差,Z称为这位学生的标准分),转化成标准分后可能出现小数或负数,因此,又常常再将Z分数作线性变换转化成其他分数。例如某次学业选拔考试采用的是T分数,线性变换公式是:,已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25,则该考生的T分数为____________________.
江苏省南通中学高二期中考试数学答题纸
一、选择题答案(每题5分)
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题答案(每题6分)
11、 12、 13、
14、 15、 16、
三、解答题(本大题共6小题、共74分,解答给出文字说明,演算步骤)
17.(本小题满分14分,第一、二小问满分各7分)某热水瓶胆生产厂生产的10件产品中,有8件一级品,2件二级品,一级品和二级品在外观上没有区别.从这10件产品中任意抽检2件,计算:(1)2件都是一级品的概率;(2)至少有一件二级品的概率.
18.(本小题满分15分,第一、二小问满分分别是7分、8分)
已知算法:(1)指出其功能(用算式表示),
(2)将该算法用流程图描述之。
19.(本小题满分14分,第一、二小问满分各7分)
设F1、F2分别为椭圆C: =1(a>b>0)的左、右两个焦点.
(1)若椭圆C上的点A(1,)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程;
20.(本小题满分15分,第一、二小问满分分别是7、8分)
已知,根据下列条件求为钝角三角形的概率:
在线段OB上任取一点C;
过点A任作一直线与直线OB交于点C.
21.(本小题满分16分,第一、二小问满分各8分)
设A、B是椭圆上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(1)确定的取值范围,并求直线AB的方程;
(2)试判断是否存在这样的,使得A、B、C、D四点在同一个圆上?并说明理由.
高二年级第一学期期中考试答案
选择题
AACDC ABDDA
二、填空题
11.甲; 12.m=0 ; 13. ;
14.充分非必要; 15. 有且仅有两条; 16、84
三、解答题
17. 解: (1)设2件都是一级品为事件A.……………………………1分
从10件产品中抽取2件,共有45个基本事件,且都是等可能的3分
而事件A的结果(即包含的基本事件数)有28种, ……… …5分
则P(A)=. ………………………………………………7分
(2)设至少有一件二级品为事件B,……………………………………8分
则B是两个互斥事件:“抽取的2件产品中包含了一件一级品,一件二级品(记为B1)”与“抽取的2件产品均为二级品(B2)”的和. ………9分
而P(B1)=,P(B2)=, …………………10分
∴P(B)=P(B1+B2)= P(B1)+ P(B2) ……………11分
=. …………………………………13分
答: 2件都是一级品的概率为;至少有一件二级品的概率为.14分
18.解:算法的功能为:……………………………7分
程序框图为:
………………………………………………15分
19.解:(1)椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.又点A(1,)在椭圆上,因此=1得b2=3,于是c2=1.…4分
所以椭圆C的方程为=1,………5分
焦点F1(-1,0),F2(1,0). ……………7分
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:
, 即x1=2x+1,y1=2y.…………10分
因此=1.即为所求的轨迹方程. ……………14分
20. 解:(1); (2).
21. (1)依题意,可设直线AB的方程为,整理得 ①
设①的两个不同的根, ② …………4分
是线段AB的中点,得解得k=-1,代入②得,>12,即的取值范围是(12,+).……6分
于是,直线AB的方程为………8分
(2)代入椭圆方程,整理得 ③
③的两根,
于是由弦长公式可得 ④……10分
将直线AB的方程 ⑤
同理可得 ⑥
……12分
假设在>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.点M到直线AB的距离为 ⑦
于是,由④、⑥、⑦式和勾股定理可得
故当时,A、B、C、D四点均在以M为圆心,为半径的圆上.……16分
