第27章《相似》单元复习测试题(含答案)
文档属性
| 名称 | 第27章《相似》单元复习测试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 532.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学第二十七章《相似》单元复习测试题(含答案)
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中,属于相似图形的是( )
2.下列各组线段中,是成比例线段的是( )
A.2,3,5,6 B.1,2,3,5
C.1,3,3,7 D.2,3,4,6
3.如题3图,已知AB∥CD∥EF.若AC=6,CE=2,BD=3,则BF的长为( )
题3图
A.6 B.5.5 C.4 D.4.5
4.一个多边形放大4倍后,得到的图形与原图形相比,下列说法中正确的是( )
A.周长扩大16倍 B.周长缩小16倍
C.面积扩大16倍 D.面积缩小16倍
5.已知△ABC∽△DEF,∠A=∠D=70°,∠B=60°,则∠F=( )
A.50° B.60° C.70° D.50°或60°
6.△OAB的顶点坐标分别为O(0,0),A(2,4),B(4,0),△OCD与△OAB是以点O为位似中心的位似图形,其中点A与点C对应,相似比为 ,则点C的坐标是( )
A.(1,2) B.(4,8)
C.(1,2)或(-1,-2) D.(4,8)或(-4,-8)
7.如题7图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
题7图
A.6cm B.12cm C.21cm D.24cm
8.如题8图,点P在△ABC的边AC上,若只添加一个条件,就可以判定△ABP∽△ACB,则下列添加的条件中,不正确的是( )
题8图
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
9.如题9图,有一块直角三角形余料ABC,∠BAC=90°,G,D分别是AB,AC边上的点,现从中截一矩形DEFG,其中点E,F在BC边上.若AB=8cm,AC=6cm,EF=2DE,则GF的长为( )
题9图
A.cm B.3cm C.cm D.cm
10.如题10图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠C=∠E;②△ADE∽△FDB;③∠AFE=∠AFC; ④FD=FB.其中正确的结论是( )
题10图
A.①② B.①③ C.②③ D.③④
二、填空题(本大题7小题,每小题4分,共28分)
11.在一幅比例尺为1∶60000的地图上,甲、乙两地的距离为10cm,则两地的实际距离为________km.
12.如题12图,∠C=∠E=90°,AC=4,BC=8,AE=3,则AD=________.
题12图
13.如题13图,在 ABCD中,E为AD延长线上一点,且BC=2DE,连接BE,交DC于点F.若CF=2,则CD的长为________.
题13图
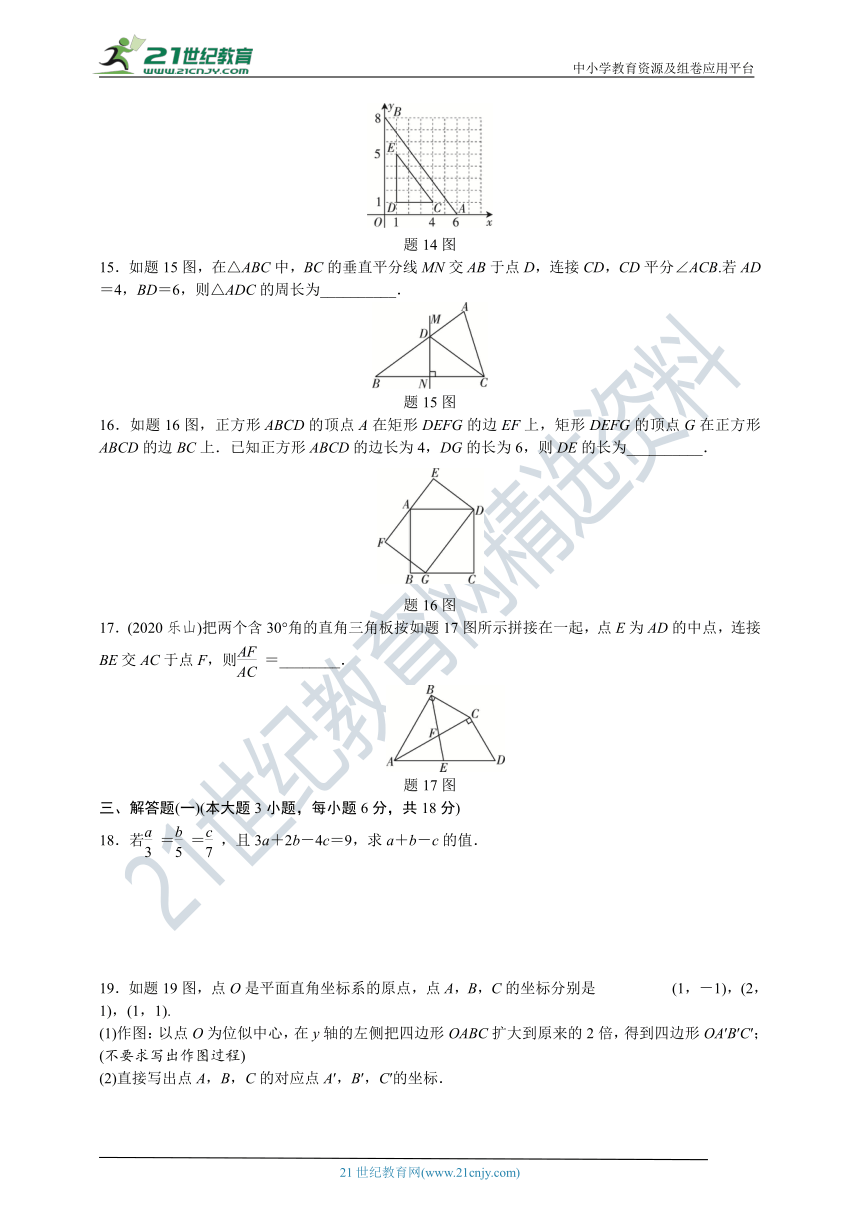
14.如题14图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作△AOB的位似图形△CDE,则位似中心的坐标为__________.
题14图
15.如题15图,在△ABC中,BC的垂直平分线MN交AB于点D,连接CD,CD平分∠ACB.若AD=4,BD=6,则△ADC的周长为__________.
题15图
16.如题16图,正方形ABCD的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形ABCD的边BC上.已知正方形ABCD的边长为4,DG的长为6,则DE的长为__________.
题16图
17.(2020乐山)把两个含30°角的直角三角板按如题17图所示拼接在一起,点E为AD的中点,连接BE交AC于点F,则=________.
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.若==,且3a+2b-4c=9,求a+b-c的值.
19.如题19图,点O是平面直角坐标系的原点,点A,B,C的坐标分别是 (1,-1),(2,1),(1,1).
(1)作图:以点O为位似中心,在y轴的左侧把四边形OABC扩大到原来的2倍,得到四边形OA′B′C′;(不要求写出作图过程)
(2)直接写出点A,B,C的对应点A′,B′,C′的坐标.
题19图
20.如题20图,在 ABCD中,E是DC上一点,连接AE,BE,F为AE上一点,连接BF,且∠BFE=∠C.求证:△ABF∽△EAD.
题20图
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如题21图,小明在水平地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,当镜子与小明的距离DE=2米时,小明刚好从镜子中看到铁塔的顶端A.已知小明的眼睛距地面的高度CD=1.6米,求铁塔AB的高度.(根据光的反射原理知∠1=∠2)
题21图
22.如题22图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,点F在边AB上,BC2=BF·BA,CF与DE相交于点G.
(1)求证:△BCF∽△DGF;
(2)若DF=3,4AB=5BC,求DG的长.
题22图
23.如题23图,AB是⊙M的直径,BC是⊙M的切线,切点为B,连接CM交⊙M于点G,过点C作DC⊥BC交BG的延长线于点D,连接AG并延长,交BC于点E.
(1)求证:△ABE∽△BCD;
(2)若MB=BE=1,求GE的长.
题23图
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如题24图,在四边形ABCD中,AB=4,BC=7,∠B=∠C=60°,P为BC边上一点(不与点B,C重合),连接AP,过点P作PE交DC于点E,使得 ∠APE=∠B.
(1)△ABP与△PCE相似吗?为什么?
(2)若BP=5,求CE的长.
(3)当BP为多少时,CE的长最大?最大为多少?
题24图
25.如题25图,直线y=-x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式.
(2)M(m,0)为线段OA上一动点(不与点O,A重合),过点M作垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①用含m的代数式表示线段PN的长;
②若以点B,P,N为顶点的三角形与△APM相似,求点M的坐标.
题25图
参考答案
1.D 2.D 3.C 4.C 5.A 6.C 7.C 8.D 9.A 10.C
11.6 12.3 13.3 14.(2,2) 15.10+2 16. 17.
18.解:设 ===k,则a=3k,b=5k,c=7k.
∵3a+2b-4c=9,
∴9k+10k-28k=9,即-9k=9.解得k=-1.
∴a=-3,b=-5,c=-7.
∴a+b-c=-3-5-(-7)=-1.
19.解:(1)如答题19图,四边形OA′B′C′即为所求.
答题19图
(2)A′(-2,2),B′(-4,-2),C′(-2,-2).
20.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠BAF=∠AED,∠D+∠C=180°.
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D.∴△ABF∽△EAD.
21.解:∵∠1=∠2,∴∠CED=∠AEB.
由题意,得CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°.
∴△CDE∽△ABE.∴=.
∵DE=2,BE=20,CD=1.6,
∴=.∴AB=16.
答:铁塔AB的高度为16米.
22.(1)证明:∵DE∥BC,∴△BCF∽△DGF.
(2)解:∵BC2=BF·BA,∴=.
又∠ABC=∠CBF,∴△BAC∽△BCF.
由(1)知△BCF∽△DGF,∴△DGF∽△BAC.
∴=,即=.
∵4AB=5BC,∴=.
∵DF=3,∴DG=×3=.
23.(1)证明:∵BC是⊙M的切线,∴∠ABE=90°.
∵DC⊥BC,∴∠BCD=90°.
∴∠ABE=∠BCD.
∵AB是⊙M的直径,∴∠AGB=90°.
∴∠A+∠ABG=90°.
∵∠CBD+∠ABG=∠ABE=90°,
∴∠A=∠CBD.
∴△ABE∽△BCD.
(2)解:∵MB=1,∴AB=2.
在Rt△ABE中,∠ABE=90°,BE=1,AB=2,
∴AE==.
∵S△ABE=AB·BE=BG·AE,
∴BG==.
在Rt△BGE中,∠BGE=180°-∠AGB=90°,
∴GE==.
24.解:(1)△ABP与△PCE相似.理由如下:
∵∠B=∠C=60°,∠APE=∠B,
∴∠APE=∠B=∠C=60°.
∴∠BPA+∠EPC=∠EPC+∠CEP=120°.
∴∠BPA=∠CEP.∴△ABP∽△PCE.
(2)由(1)可知△ABP∽△PCE,∴=.
∵BC=7,BP=5,∴PC=BC-BP=7-5=2.
∴=.解得CE=.
(3)设BP=x(0<x<7),CE=y,则PC=7-x.
由(1)可知△ABP∽△PCE,
∴=.∴=.
∴y=-x2+x=-+.
∵-<0,0<x<7,
∴当x=时,y有最大值,最大值为.
即当BP为时,CE的长最大,最大为.
25.解:(1)将A(3,0)代入y=- x+c,得0=-4+c.
解得c=4.
∴y=- x+4.令x=0,得y=4.
∴B(0,4).
将A(3,0),B(0,4)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+ x+4.
(2)①∵M(m,0),MN⊥x轴,
∴P,N.
∴PN=-m2+m+4+m-4=-m2+8m(0<m<3).
②∵△BPN和△APM相似,∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°.
(i)当∠BNP=90°时,如答题25图(1),则有BN⊥MN.
∴点N的纵坐标为4.
∴-m2+ m+4=4.解得m1=0(舍去),m2=.
∴M.
答题25图(1) 答题25图(2)
(ii)当∠NBP=90°时,如答题25图(2),过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=-m2+m+4-4=-m2+m.
∵∠NBP=90°,∴∠NBC+∠ABO=90°.∴∠BNC=∠ABO.
又∠NCB=∠BOA=90°,∴△NCB∽△BOA.∴=.
∵A(3,0),B(0,4),∴AO=3,BO=4.∴=.
解得m3=0(舍去),m4= .
∴M.
综上,点M的坐标为或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二十七章《相似》单元复习测试题(含答案)
一、选择题(本大题10小题,每小题3分,共30分)
1.下列图形中,属于相似图形的是( )
2.下列各组线段中,是成比例线段的是( )
A.2,3,5,6 B.1,2,3,5
C.1,3,3,7 D.2,3,4,6
3.如题3图,已知AB∥CD∥EF.若AC=6,CE=2,BD=3,则BF的长为( )
题3图
A.6 B.5.5 C.4 D.4.5
4.一个多边形放大4倍后,得到的图形与原图形相比,下列说法中正确的是( )
A.周长扩大16倍 B.周长缩小16倍
C.面积扩大16倍 D.面积缩小16倍
5.已知△ABC∽△DEF,∠A=∠D=70°,∠B=60°,则∠F=( )
A.50° B.60° C.70° D.50°或60°
6.△OAB的顶点坐标分别为O(0,0),A(2,4),B(4,0),△OCD与△OAB是以点O为位似中心的位似图形,其中点A与点C对应,相似比为 ,则点C的坐标是( )
A.(1,2) B.(4,8)
C.(1,2)或(-1,-2) D.(4,8)或(-4,-8)
7.如题7图,放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.若光源到幻灯片的距离为30cm,到屏幕的距离为90cm,且幻灯片中的图形的高度为7cm,则屏幕上图形的高度为( )
题7图
A.6cm B.12cm C.21cm D.24cm
8.如题8图,点P在△ABC的边AC上,若只添加一个条件,就可以判定△ABP∽△ACB,则下列添加的条件中,不正确的是( )
题8图
A.∠ABP=∠C B.∠APB=∠ABC
C.= D.=
9.如题9图,有一块直角三角形余料ABC,∠BAC=90°,G,D分别是AB,AC边上的点,现从中截一矩形DEFG,其中点E,F在BC边上.若AB=8cm,AC=6cm,EF=2DE,则GF的长为( )
题9图
A.cm B.3cm C.cm D.cm
10.如题10图,△ABC与△AEF中,AB=AE,BC=EF,∠B=∠E,AB交EF于点D.给出下列结论:①∠C=∠E;②△ADE∽△FDB;③∠AFE=∠AFC; ④FD=FB.其中正确的结论是( )
题10图
A.①② B.①③ C.②③ D.③④
二、填空题(本大题7小题,每小题4分,共28分)
11.在一幅比例尺为1∶60000的地图上,甲、乙两地的距离为10cm,则两地的实际距离为________km.
12.如题12图,∠C=∠E=90°,AC=4,BC=8,AE=3,则AD=________.
题12图
13.如题13图,在 ABCD中,E为AD延长线上一点,且BC=2DE,连接BE,交DC于点F.若CF=2,则CD的长为________.
题13图
14.如题14图,在平面直角坐标系中,已知点O(0,0),A(6,0),B(0,8),以某点为位似中心,作△AOB的位似图形△CDE,则位似中心的坐标为__________.
题14图
15.如题15图,在△ABC中,BC的垂直平分线MN交AB于点D,连接CD,CD平分∠ACB.若AD=4,BD=6,则△ADC的周长为__________.
题15图
16.如题16图,正方形ABCD的顶点A在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形ABCD的边BC上.已知正方形ABCD的边长为4,DG的长为6,则DE的长为__________.
题16图
17.(2020乐山)把两个含30°角的直角三角板按如题17图所示拼接在一起,点E为AD的中点,连接BE交AC于点F,则=________.
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.若==,且3a+2b-4c=9,求a+b-c的值.
19.如题19图,点O是平面直角坐标系的原点,点A,B,C的坐标分别是 (1,-1),(2,1),(1,1).
(1)作图:以点O为位似中心,在y轴的左侧把四边形OABC扩大到原来的2倍,得到四边形OA′B′C′;(不要求写出作图过程)
(2)直接写出点A,B,C的对应点A′,B′,C′的坐标.
题19图
20.如题20图,在 ABCD中,E是DC上一点,连接AE,BE,F为AE上一点,连接BF,且∠BFE=∠C.求证:△ABF∽△EAD.
题20图
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如题21图,小明在水平地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,当镜子与小明的距离DE=2米时,小明刚好从镜子中看到铁塔的顶端A.已知小明的眼睛距地面的高度CD=1.6米,求铁塔AB的高度.(根据光的反射原理知∠1=∠2)
题21图
22.如题22图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,点F在边AB上,BC2=BF·BA,CF与DE相交于点G.
(1)求证:△BCF∽△DGF;
(2)若DF=3,4AB=5BC,求DG的长.
题22图
23.如题23图,AB是⊙M的直径,BC是⊙M的切线,切点为B,连接CM交⊙M于点G,过点C作DC⊥BC交BG的延长线于点D,连接AG并延长,交BC于点E.
(1)求证:△ABE∽△BCD;
(2)若MB=BE=1,求GE的长.
题23图
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如题24图,在四边形ABCD中,AB=4,BC=7,∠B=∠C=60°,P为BC边上一点(不与点B,C重合),连接AP,过点P作PE交DC于点E,使得 ∠APE=∠B.
(1)△ABP与△PCE相似吗?为什么?
(2)若BP=5,求CE的长.
(3)当BP为多少时,CE的长最大?最大为多少?
题24图
25.如题25图,直线y=-x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=-x2+bx+c经过点A,B.
(1)求点B的坐标和抛物线的解析式.
(2)M(m,0)为线段OA上一动点(不与点O,A重合),过点M作垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
①用含m的代数式表示线段PN的长;
②若以点B,P,N为顶点的三角形与△APM相似,求点M的坐标.
题25图
参考答案
1.D 2.D 3.C 4.C 5.A 6.C 7.C 8.D 9.A 10.C
11.6 12.3 13.3 14.(2,2) 15.10+2 16. 17.
18.解:设 ===k,则a=3k,b=5k,c=7k.
∵3a+2b-4c=9,
∴9k+10k-28k=9,即-9k=9.解得k=-1.
∴a=-3,b=-5,c=-7.
∴a+b-c=-3-5-(-7)=-1.
19.解:(1)如答题19图,四边形OA′B′C′即为所求.
答题19图
(2)A′(-2,2),B′(-4,-2),C′(-2,-2).
20.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠BAF=∠AED,∠D+∠C=180°.
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠AFB=∠D.∴△ABF∽△EAD.
21.解:∵∠1=∠2,∴∠CED=∠AEB.
由题意,得CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°.
∴△CDE∽△ABE.∴=.
∵DE=2,BE=20,CD=1.6,
∴=.∴AB=16.
答:铁塔AB的高度为16米.
22.(1)证明:∵DE∥BC,∴△BCF∽△DGF.
(2)解:∵BC2=BF·BA,∴=.
又∠ABC=∠CBF,∴△BAC∽△BCF.
由(1)知△BCF∽△DGF,∴△DGF∽△BAC.
∴=,即=.
∵4AB=5BC,∴=.
∵DF=3,∴DG=×3=.
23.(1)证明:∵BC是⊙M的切线,∴∠ABE=90°.
∵DC⊥BC,∴∠BCD=90°.
∴∠ABE=∠BCD.
∵AB是⊙M的直径,∴∠AGB=90°.
∴∠A+∠ABG=90°.
∵∠CBD+∠ABG=∠ABE=90°,
∴∠A=∠CBD.
∴△ABE∽△BCD.
(2)解:∵MB=1,∴AB=2.
在Rt△ABE中,∠ABE=90°,BE=1,AB=2,
∴AE==.
∵S△ABE=AB·BE=BG·AE,
∴BG==.
在Rt△BGE中,∠BGE=180°-∠AGB=90°,
∴GE==.
24.解:(1)△ABP与△PCE相似.理由如下:
∵∠B=∠C=60°,∠APE=∠B,
∴∠APE=∠B=∠C=60°.
∴∠BPA+∠EPC=∠EPC+∠CEP=120°.
∴∠BPA=∠CEP.∴△ABP∽△PCE.
(2)由(1)可知△ABP∽△PCE,∴=.
∵BC=7,BP=5,∴PC=BC-BP=7-5=2.
∴=.解得CE=.
(3)设BP=x(0<x<7),CE=y,则PC=7-x.
由(1)可知△ABP∽△PCE,
∴=.∴=.
∴y=-x2+x=-+.
∵-<0,0<x<7,
∴当x=时,y有最大值,最大值为.
即当BP为时,CE的长最大,最大为.
25.解:(1)将A(3,0)代入y=- x+c,得0=-4+c.
解得c=4.
∴y=- x+4.令x=0,得y=4.
∴B(0,4).
将A(3,0),B(0,4)代入y=-x2+bx+c,
得解得
∴抛物线的解析式为y=-x2+ x+4.
(2)①∵M(m,0),MN⊥x轴,
∴P,N.
∴PN=-m2+m+4+m-4=-m2+8m(0<m<3).
②∵△BPN和△APM相似,∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°.
(i)当∠BNP=90°时,如答题25图(1),则有BN⊥MN.
∴点N的纵坐标为4.
∴-m2+ m+4=4.解得m1=0(舍去),m2=.
∴M.
答题25图(1) 答题25图(2)
(ii)当∠NBP=90°时,如答题25图(2),过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=-m2+m+4-4=-m2+m.
∵∠NBP=90°,∴∠NBC+∠ABO=90°.∴∠BNC=∠ABO.
又∠NCB=∠BOA=90°,∴△NCB∽△BOA.∴=.
∵A(3,0),B(0,4),∴AO=3,BO=4.∴=.
解得m3=0(舍去),m4= .
∴M.
综上,点M的坐标为或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
