第24章《圆》单元复习测试题(含答案)
文档属性
| 名称 | 第24章《圆》单元复习测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 571.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-12 14:19:33 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学第二十四章《圆》单元复习测试题(含答案)
一、选择题(本大题10小题,每小题3分,共30分)
1.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
2.已知⊙O的半径为4,点O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.在圆内接四边形ABCD中,∠A=80°,则∠A的对角∠C=( )
A.20° B.40° C.80° D.100°
4.如题4图,在⊙O中,=.若∠B=75°,则∠A的度数为( )
题4图
A.15° B.30° C.75° D.60°
5.如题5图,AB为⊙O的直径,点C,D在⊙O上.若∠CAB=36°,则∠D的度数为( )
题5图
A.72° B.54° C.45° D.36°
6.已知半径为9的扇形的弧长为6π,该扇形的面积为( )
A.18π B.27π C.36π D.54π
7.如题7图,点I为△ABC的外心,且∠BIC=150°,则∠A的度数为( )
题7图
A.70° B.75° C.140° D.150°
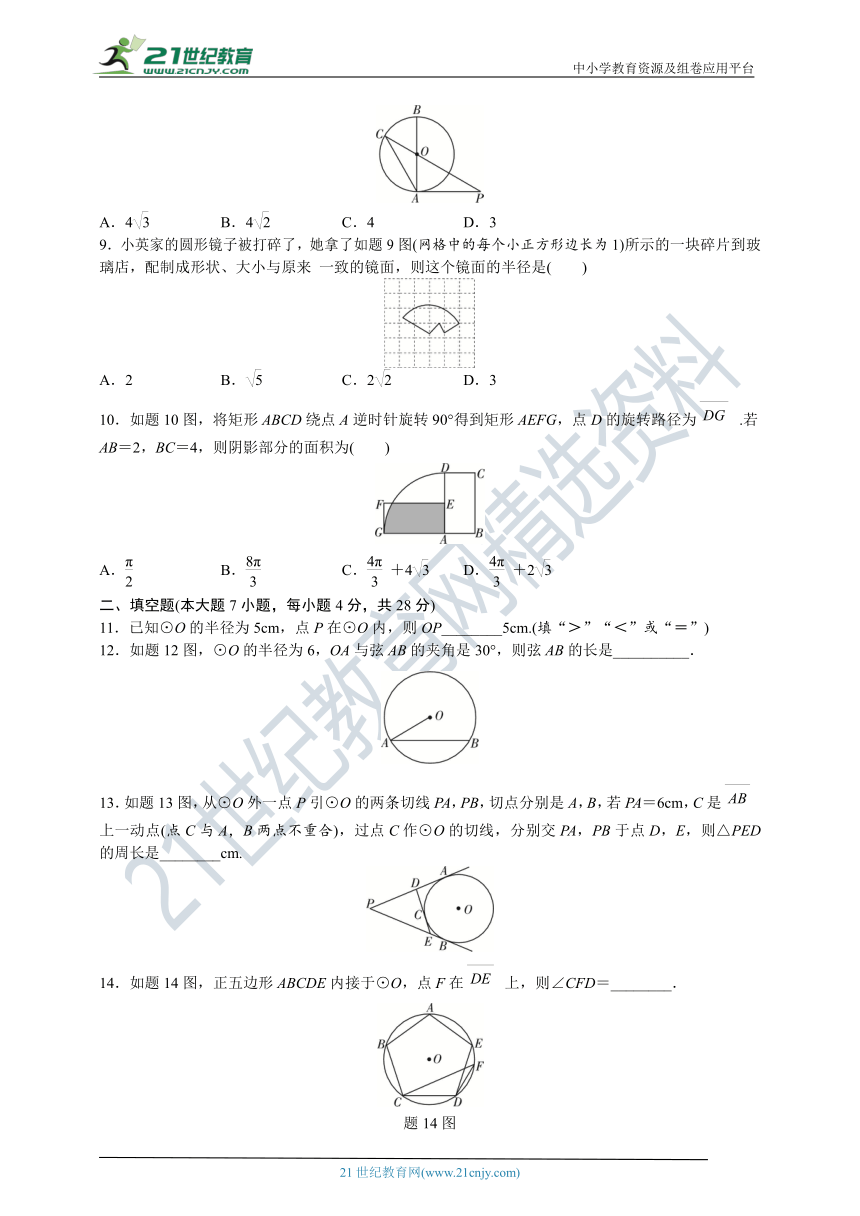
8.如题8图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长,交⊙O于点C,连接AC.若AB=8,∠P=30°,则AC=( )
A.4 B.4 C.4 D.3
9.小英家的圆形镜子被打碎了,她拿了如题9图(网格中的每个小正方形边长为1)所示的一块碎片到玻璃店,配制成形状、大小与原来 一致的镜面,则这个镜面的半径是( )
A.2 B. C.2 D.3
10.如题10图,将矩形ABCD绕点A逆时针旋转90°得到矩形AEFG,点D的旋转路径为.若AB=2,BC=4,则阴影部分的面积为( )
A. B. C.+4 D.+2
二、填空题(本大题7小题,每小题4分,共28分)
11.已知⊙O的半径为5cm,点P在⊙O内,则OP________5cm.(填“>”“<”或“=”)
12.如题12图,⊙O的半径为6,OA与弦AB的夹角是30°,则弦AB的长是__________.
13.如题13图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,若PA=6cm,C是上一动点(点C与A,B两点不重合),过点C作⊙O的切线,分别交PA,PB于点D,E,则△PED的周长是________cm.
14.如题14图,正五边形ABCDE内接于⊙O,点F在上,则∠CFD=________.
题14图
15.用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝处忽略不计),则这个圆锥的底面圆的半径为________.
16.如题16图,AB是⊙O的弦,AB=8,C是⊙O上一动点,且∠ACB=45°.若点M,N分别是AB,AC的中点,则MN长的最大值是________.
题16图
17.如题17图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,直线MN与l1相交于点M,与l2相交于点N,⊙O的半径为1,∠1=60°,直线MN从图中位置向右平移.下列结论:①l1和l2的距离为2;②MN=;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=时,直线MN与⊙O相切.其中正确的结论是____________.(填序号)
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.如题18图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD.
题18图
19.用铁皮制作如题19图所示的圆锥形容器盖,求这个容器盖所需铁皮的面积(结果保留π),并求制作容器盖的扇形的圆心角.
题19图
20.如题20图,在△ABC中,AB=AC.
(1)求作一点P,使得点P为△ABC外接圆的圆心;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接AP,BP,延长AP交BC于点D,若∠BAC=50°,求∠PBC的度数.
题20图
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如题21图,隧道的截面由半圆和矩形构成,矩形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?请说明理由.
题21图
22.如题22图,已知△ABC内接于⊙O,AD为⊙O的直径,点C在劣弧AB上(不与点A,B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:
α 30° 35° 40° 50° 60° 80°
β 120° 125° 130° 140° 150° 170°
试判断α与β之间的关系,并给出证明.
题22图
23.在如题23图所示的网格中,每个小正方形的顶点叫格点,且边长均为1,△ABC的三个顶点均在格点上,以点A为圆心的与BC相切于点D,分别交AB,AC于点E,F.
(1)求△ABC三边的长;
(2)求图中由线段EB,BC,CF及所围成的阴影部分的面积.
题23图
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如题24图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E,D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①AB是⊙O的切线;
②∠EDC=∠FDC.
(2)求CD的长.
题24图
25.阅读以下材料,并回答问题:
若一个三角形两边平方的和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是________命题;(填“真”或“假”)
(2)在△ABC中,∠C=90°,△ABC的内角∠A,∠B,∠C所对边的长分别为a,b,c,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c的值;
(3)如题25图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A,B不重合),D是的中点,点C,D在直径AB的两侧,若存在点E,使得AE=AD,CB=CE.求证:△ACE是奇异三角形.
题25图
参考答案
1.D 2.A 3.D 4.B 5.B 6.B 7.B 8.A 9.B 10.D
11.< 12.6 13.12 14.36° 15.1 16.4 17.①②③④
18.证明:∵BD=AC,∴=.
∴-=-,即=.
∴AB=CD.
19.解:由图可知圆锥的底面圆的直径为80 cm,母线长为50 cm,
∴圆锥的底面圆的周长为80π cm.
∴圆锥形容器盖的侧面展开图的弧长为80π cm.
∴面积为 ×80π×50=2 000π(cm2).
设制作容器盖的扇形的圆心角为n°.
∴=80π.
解得n=288.
答:这个容器盖所需铁皮的面积为2 000π cm2,制作容器盖的扇形的圆心角为288°.
20.解:(1)如答题20图,点P即为△ABC外接圆的圆心.
答题20图
(2)∵点P为△ABC外接圆的圆心,AB=AC,∠BAC=50°,
∴AD⊥BC,∠BAP=∠CAP=25°,PA=PB.
∴∠BPD=2∠BAP=50°,∠BDP=90°.
∴∠PBD=90°-50°=40°,即∠PBC=40°.
21.解:这辆货运卡车能通过该隧道.理由如下:
如答题21图,设点O为AD的中点,在AD上取点G,使得OG=2.3,过点G作GF⊥BC于点F,延长FG交半圆于点E,则GF=AB=3,半圆的半径OE=AD=BC=6.
答题21图
∴EG==≈5.54.
∴EF=EG+GF≈5.54+3=8.54>8.
∴这辆货运卡车能通过该隧道.
22.解:β-α=90°.
证明:如答题22图,连接BD.
答题22图
∵AD为⊙O的直径,∴∠DBA=90°.
∵∠DAB=α,∴∠D=90°-α.
∵B,D,A,C四点共圆,
∴∠ACB+∠D=180°.
∵∠ACB=β,∴β+90°-α=180°.∴β-α=90°.
23.解:(1)由图可得AB==2,AC==2,
BC==4.
(2)由(1)得AB2+AC2=(2)2+(2)2=(4)2=BC2.
∴∠BAC=90°.
如答题23图,连接AD,则AD⊥BC,BD=DC=BC=2.
答题23图
∴AD===2.
∴S阴=S△ABC-S扇形AEF=AB·AC-·AD2=20-5π.
24.(1)证明:①如答题24图,连接OC.
∵OA=OB,CA=CB,∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
②∵OA=OB,CA=CB,∴∠AOC=∠BOC.
∴=.∴∠EDC=∠FDC.
答题24图
(2)解:如答题24图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,OD=OF,DF=6,
∴DN=NF=DF=3,∠DON=∠FON.
在Rt△ODN中,OD=DE=5,DN=3,
∴ON==4.
∵∠AOC=∠BOC,∠DON=∠FON,
∴∠BOC+∠FON=×180°=90°.
∴∠OCM=∠CON=∠MNO=90°.
∴四边形OCMN是矩形.
∴CM=ON=4,MN=OC=DE=5.
在Rt△CDM中,CM=4,DM=DN+MN=8,
∴CD===4.
25.(1)解:真.
(2)解:∵∠C=90°,∴a2+b2=c2.①
∵Rt△ABC是奇异三角形,且b>a,∴a2+c2=2b2.②
由①②,得b=a,c=a.∴a∶b∶c=1∶∶.
(3)证明:如答题25图,连接BD.
答题25图
∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+CB2=AB2,
在Rt△ADB中,AD2+BD2=AB2.
∵点D是的中点,∴=.∴AD=BD.
∴AB2=AD2+BD2=2AD2.∴AC2+CB2=2AD2.
又CB=CE,AE=AD,∴AC2+CE2=2AE2.
∴△ACE是奇异三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学第二十四章《圆》单元复习测试题(含答案)
一、选择题(本大题10小题,每小题3分,共30分)
1.已知AB是半径为6的圆的一条弦,则AB的长不可能是( )
A.8 B.10 C.12 D.14
2.已知⊙O的半径为4,点O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
3.在圆内接四边形ABCD中,∠A=80°,则∠A的对角∠C=( )
A.20° B.40° C.80° D.100°
4.如题4图,在⊙O中,=.若∠B=75°,则∠A的度数为( )
题4图
A.15° B.30° C.75° D.60°
5.如题5图,AB为⊙O的直径,点C,D在⊙O上.若∠CAB=36°,则∠D的度数为( )
题5图
A.72° B.54° C.45° D.36°
6.已知半径为9的扇形的弧长为6π,该扇形的面积为( )
A.18π B.27π C.36π D.54π
7.如题7图,点I为△ABC的外心,且∠BIC=150°,则∠A的度数为( )
题7图
A.70° B.75° C.140° D.150°
8.如题8图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长,交⊙O于点C,连接AC.若AB=8,∠P=30°,则AC=( )
A.4 B.4 C.4 D.3
9.小英家的圆形镜子被打碎了,她拿了如题9图(网格中的每个小正方形边长为1)所示的一块碎片到玻璃店,配制成形状、大小与原来 一致的镜面,则这个镜面的半径是( )
A.2 B. C.2 D.3
10.如题10图,将矩形ABCD绕点A逆时针旋转90°得到矩形AEFG,点D的旋转路径为.若AB=2,BC=4,则阴影部分的面积为( )
A. B. C.+4 D.+2
二、填空题(本大题7小题,每小题4分,共28分)
11.已知⊙O的半径为5cm,点P在⊙O内,则OP________5cm.(填“>”“<”或“=”)
12.如题12图,⊙O的半径为6,OA与弦AB的夹角是30°,则弦AB的长是__________.
13.如题13图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,若PA=6cm,C是上一动点(点C与A,B两点不重合),过点C作⊙O的切线,分别交PA,PB于点D,E,则△PED的周长是________cm.
14.如题14图,正五边形ABCDE内接于⊙O,点F在上,则∠CFD=________.
题14图
15.用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面(接缝处忽略不计),则这个圆锥的底面圆的半径为________.
16.如题16图,AB是⊙O的弦,AB=8,C是⊙O上一动点,且∠ACB=45°.若点M,N分别是AB,AC的中点,则MN长的最大值是________.
题16图
17.如题17图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,直线MN与l1相交于点M,与l2相交于点N,⊙O的半径为1,∠1=60°,直线MN从图中位置向右平移.下列结论:①l1和l2的距离为2;②MN=;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=时,直线MN与⊙O相切.其中正确的结论是____________.(填序号)
题17图
三、解答题(一)(本大题3小题,每小题6分,共18分)
18.如题18图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD.
题18图
19.用铁皮制作如题19图所示的圆锥形容器盖,求这个容器盖所需铁皮的面积(结果保留π),并求制作容器盖的扇形的圆心角.
题19图
20.如题20图,在△ABC中,AB=AC.
(1)求作一点P,使得点P为△ABC外接圆的圆心;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接AP,BP,延长AP交BC于点D,若∠BAC=50°,求∠PBC的度数.
题20图
四、解答题(二)(本大题3小题,每小题8分,共24分)
21.如题21图,隧道的截面由半圆和矩形构成,矩形的长BC为12m,宽AB为3m,若该隧道内设双行道,现有一辆货运卡车高8m,宽2.3m,则这辆货运卡车能否通过该隧道?请说明理由.
题21图
22.如题22图,已知△ABC内接于⊙O,AD为⊙O的直径,点C在劣弧AB上(不与点A,B重合),设∠DAB=α,∠ACB=β,小明同学通过画图和测量得到以下近似数据:
α 30° 35° 40° 50° 60° 80°
β 120° 125° 130° 140° 150° 170°
试判断α与β之间的关系,并给出证明.
题22图
23.在如题23图所示的网格中,每个小正方形的顶点叫格点,且边长均为1,△ABC的三个顶点均在格点上,以点A为圆心的与BC相切于点D,分别交AB,AC于点E,F.
(1)求△ABC三边的长;
(2)求图中由线段EB,BC,CF及所围成的阴影部分的面积.
题23图
五、解答题(三)(本大题2小题,每小题10分,共20分)
24.如题24图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E,D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.
(1)求证:①AB是⊙O的切线;
②∠EDC=∠FDC.
(2)求CD的长.
题24图
25.阅读以下材料,并回答问题:
若一个三角形两边平方的和等于第三边平方的两倍,我们称这样的三角形为奇异三角形.
(1)命题“等边三角形一定是奇异三角形”是________命题;(填“真”或“假”)
(2)在△ABC中,∠C=90°,△ABC的内角∠A,∠B,∠C所对边的长分别为a,b,c,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c的值;
(3)如题25图,已知AB是⊙O的直径,C是⊙O上一点(点C与点A,B不重合),D是的中点,点C,D在直径AB的两侧,若存在点E,使得AE=AD,CB=CE.求证:△ACE是奇异三角形.
题25图
参考答案
1.D 2.A 3.D 4.B 5.B 6.B 7.B 8.A 9.B 10.D
11.< 12.6 13.12 14.36° 15.1 16.4 17.①②③④
18.证明:∵BD=AC,∴=.
∴-=-,即=.
∴AB=CD.
19.解:由图可知圆锥的底面圆的直径为80 cm,母线长为50 cm,
∴圆锥的底面圆的周长为80π cm.
∴圆锥形容器盖的侧面展开图的弧长为80π cm.
∴面积为 ×80π×50=2 000π(cm2).
设制作容器盖的扇形的圆心角为n°.
∴=80π.
解得n=288.
答:这个容器盖所需铁皮的面积为2 000π cm2,制作容器盖的扇形的圆心角为288°.
20.解:(1)如答题20图,点P即为△ABC外接圆的圆心.
答题20图
(2)∵点P为△ABC外接圆的圆心,AB=AC,∠BAC=50°,
∴AD⊥BC,∠BAP=∠CAP=25°,PA=PB.
∴∠BPD=2∠BAP=50°,∠BDP=90°.
∴∠PBD=90°-50°=40°,即∠PBC=40°.
21.解:这辆货运卡车能通过该隧道.理由如下:
如答题21图,设点O为AD的中点,在AD上取点G,使得OG=2.3,过点G作GF⊥BC于点F,延长FG交半圆于点E,则GF=AB=3,半圆的半径OE=AD=BC=6.
答题21图
∴EG==≈5.54.
∴EF=EG+GF≈5.54+3=8.54>8.
∴这辆货运卡车能通过该隧道.
22.解:β-α=90°.
证明:如答题22图,连接BD.
答题22图
∵AD为⊙O的直径,∴∠DBA=90°.
∵∠DAB=α,∴∠D=90°-α.
∵B,D,A,C四点共圆,
∴∠ACB+∠D=180°.
∵∠ACB=β,∴β+90°-α=180°.∴β-α=90°.
23.解:(1)由图可得AB==2,AC==2,
BC==4.
(2)由(1)得AB2+AC2=(2)2+(2)2=(4)2=BC2.
∴∠BAC=90°.
如答题23图,连接AD,则AD⊥BC,BD=DC=BC=2.
答题23图
∴AD===2.
∴S阴=S△ABC-S扇形AEF=AB·AC-·AD2=20-5π.
24.(1)证明:①如答题24图,连接OC.
∵OA=OB,CA=CB,∴OC⊥AB.
∵OC为⊙O的半径,
∴AB是⊙O的切线.
②∵OA=OB,CA=CB,∴∠AOC=∠BOC.
∴=.∴∠EDC=∠FDC.
答题24图
(2)解:如答题24图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,OD=OF,DF=6,
∴DN=NF=DF=3,∠DON=∠FON.
在Rt△ODN中,OD=DE=5,DN=3,
∴ON==4.
∵∠AOC=∠BOC,∠DON=∠FON,
∴∠BOC+∠FON=×180°=90°.
∴∠OCM=∠CON=∠MNO=90°.
∴四边形OCMN是矩形.
∴CM=ON=4,MN=OC=DE=5.
在Rt△CDM中,CM=4,DM=DN+MN=8,
∴CD===4.
25.(1)解:真.
(2)解:∵∠C=90°,∴a2+b2=c2.①
∵Rt△ABC是奇异三角形,且b>a,∴a2+c2=2b2.②
由①②,得b=a,c=a.∴a∶b∶c=1∶∶.
(3)证明:如答题25图,连接BD.
答题25图
∵AB是⊙O的直径,∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+CB2=AB2,
在Rt△ADB中,AD2+BD2=AB2.
∵点D是的中点,∴=.∴AD=BD.
∴AB2=AD2+BD2=2AD2.∴AC2+CB2=2AD2.
又CB=CE,AE=AD,∴AC2+CE2=2AE2.
∴△ACE是奇异三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
