沪科版数学七上4.5《角的大小比较与补(余)角》课件
文档属性
| 名称 | 沪科版数学七上4.5《角的大小比较与补(余)角》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 486.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-08 11:53:39 | ||
图片预览




文档简介
课件30张PPT。4.5角的大小比较与补(余)角回顾:1、1周角=______度
2、1平角=______度
3、1直角=______度
4、平角是一条直线吗?
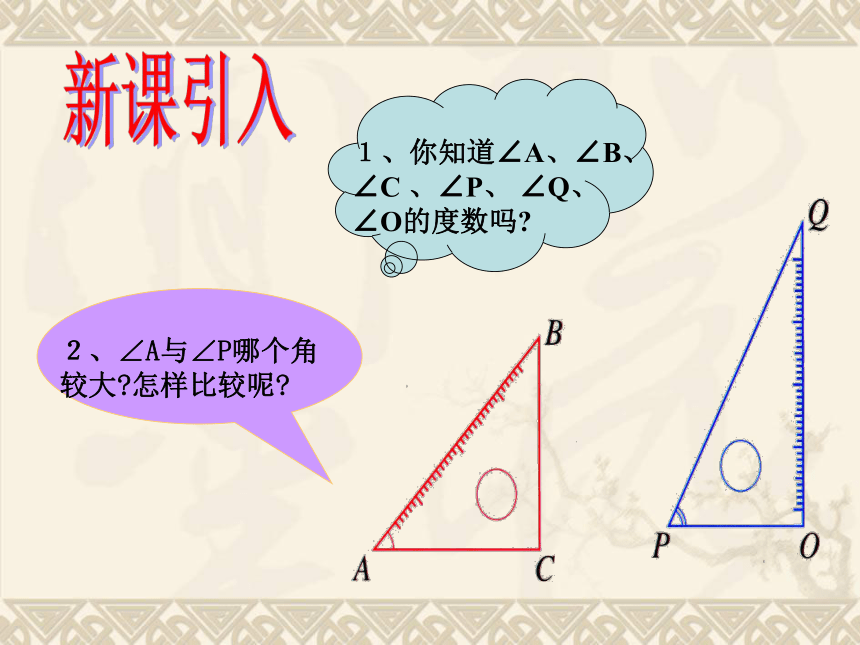
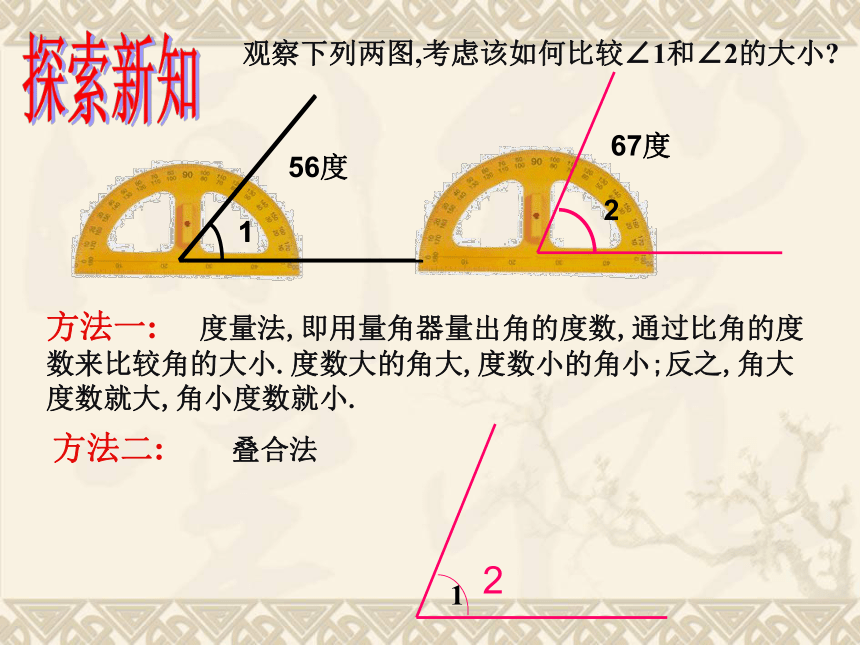
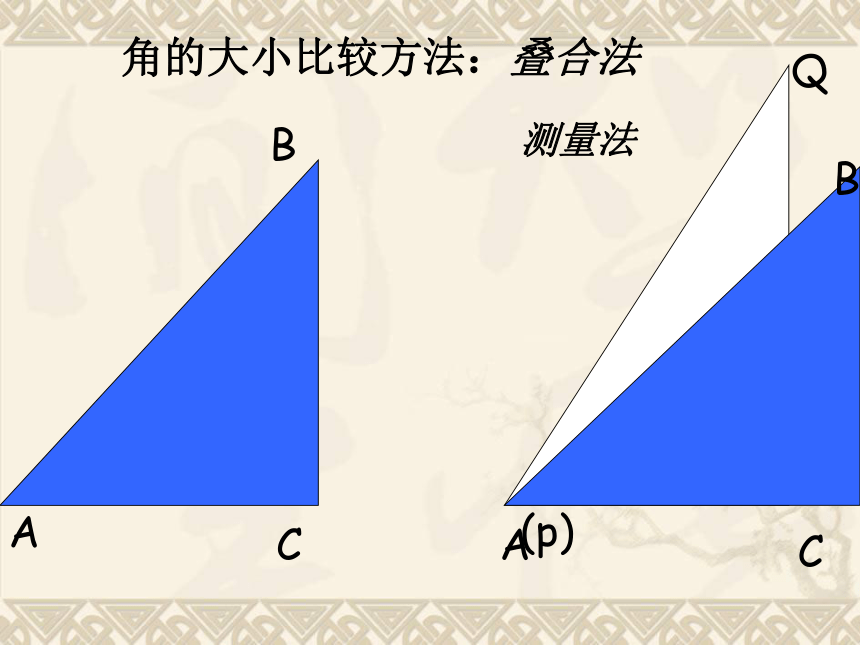
5、周角是一条射线吗?360°180°90°( )( )2、∠A与∠P哪个角较大?怎样比较呢?新课引入1267度56度方法一: 度量法,即用量角器量出角的度数,通过比角的度数来比较角的大小.度数大的角大,度数小的角小;反之,角大度数就大,角小度数就小.方法二: 叠合法1观察下列两图,考虑该如何比较∠1和∠2的大小?1探索新知BACABC(p)Q角的大小比较方法:叠合法
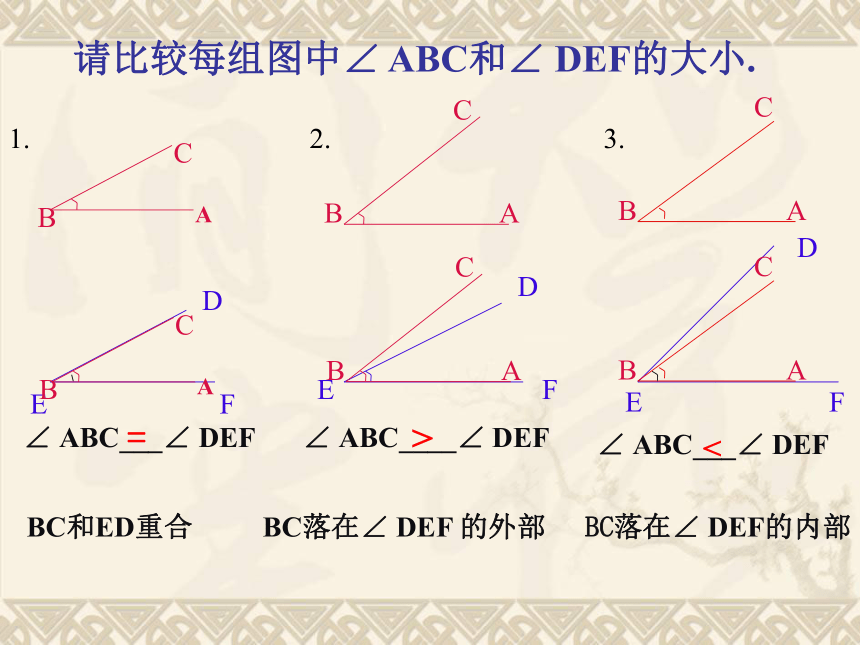
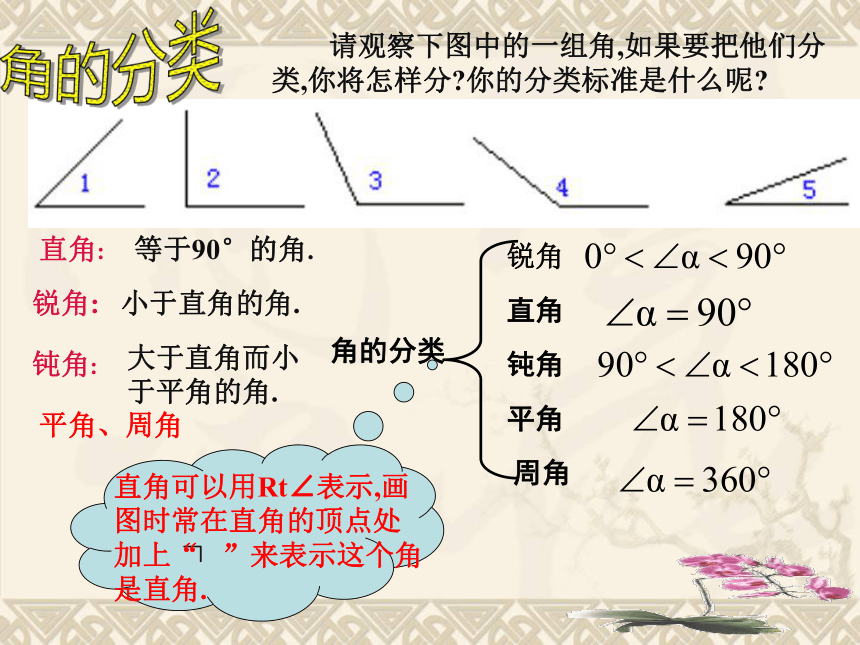
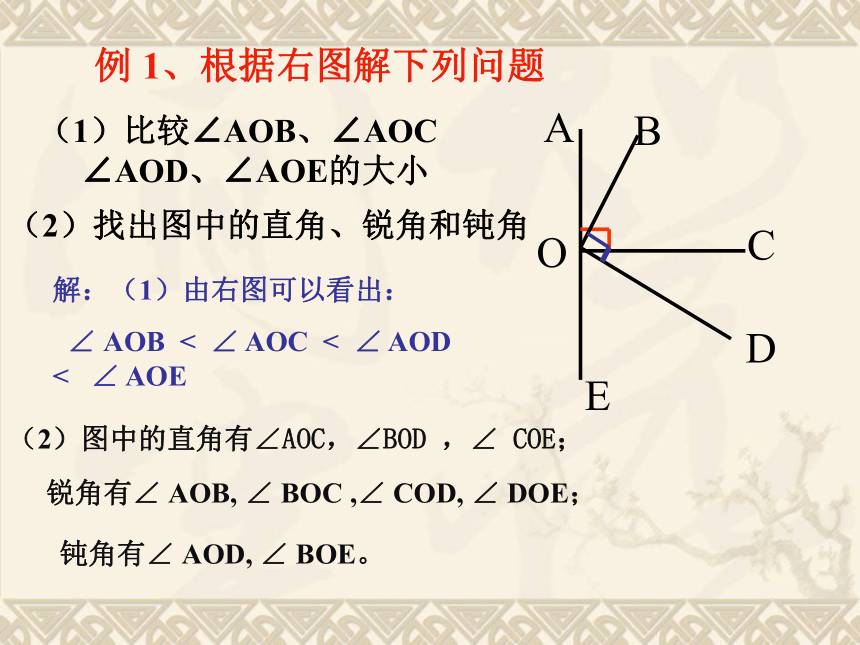
测量法请比较每组图中∠ ABC和∠ DEF的大小. BC和ED重合BC落在∠ DEF 的外部BC落在∠ DEF的内部=>< 请观察下图中的一组角,如果要把他们分类,你将怎样分?你的分类标准是什么呢? 等于90°的角.直角:小于直角的角.大于直角而小于平角的角.锐角:钝角:角的分类平角、周角 角的分类例 1、根据右图解下列问题(1)比较∠AOB、∠AOC
∠AOD、∠AOE的大小(2)找出图中的直角、锐角和钝角解:(1)由右图可以看出:
∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE(2)图中的直角有∠AOC,∠BOD ,∠ COE;锐角有∠ AOB, ∠ BOC ,∠ COD, ∠ DOE;钝角有∠ AOD, ∠ BOE。做一做 在一张透明纸上任意画一个角∠ AOB (如右图),把这张透明纸折叠,使角的两边OA和OB重合,然后把这张纸展开、铺平,画出折痕OC。 ∠ AOC与∠ BOC之间有怎样的大小关系?∠ AOC=∠ BOCOABC 从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.如果给你任意一个角∠AOB,
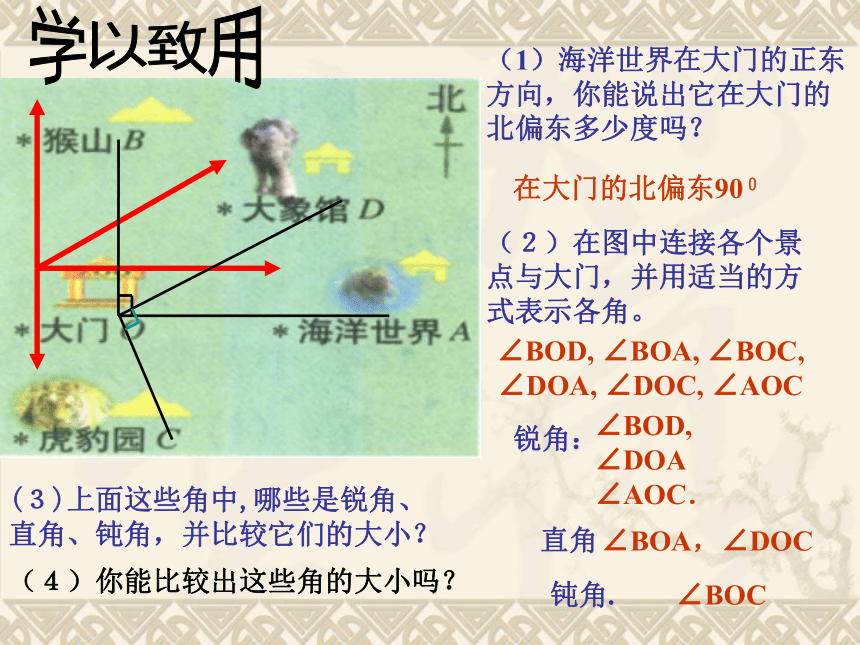
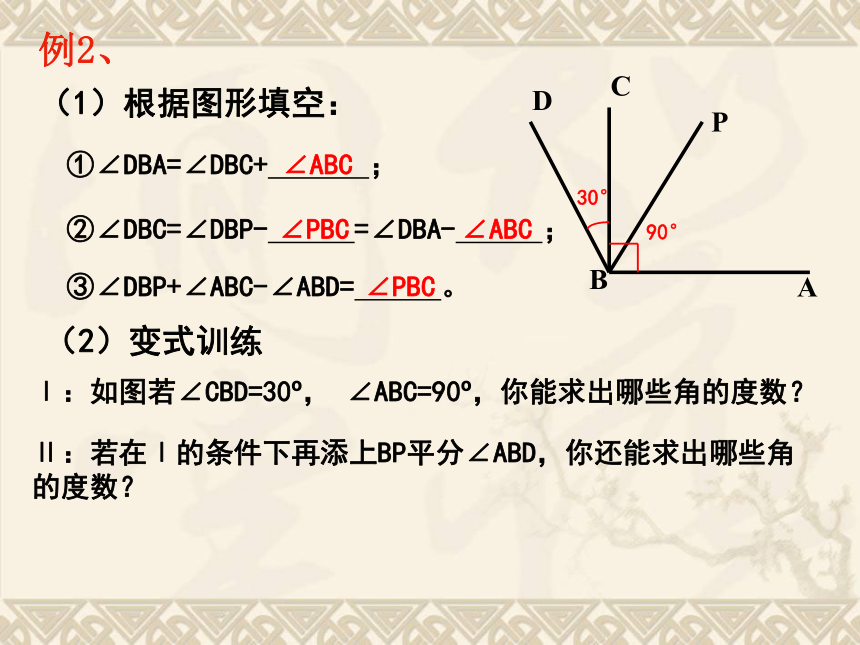
你有什么方法画出它的角平分线?AOB想一想 你会用量角器画一个角的平分线? 先用量角器量出这个角的大小,再以这个角的顶点为顶点, 一边为始边,在角的内部画一条线,使它与始边所成的角的大小是原角的一半,这条射线就是这个角的平分线。(1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?(2)在图中连接各个景点与大门,并用适当的方式表示各角。(3)上面这些角中,哪些是锐角、直角、钝角,并比较它们的大小?学以致用在大门的北偏东900∠BOD, ∠BOA, ∠BOC, ∠DOA, ∠DOC, ∠AOC∠BOC锐角:∠BOD, ∠DOA ∠AOC.∠BOA,∠DOC直角钝角.(4)你能比较出这些角的大小吗? (1)根据图形填空:①∠DBA=∠DBC+ ;②∠DBC=∠DBP- =∠DBA- ;③∠DBP+∠ABC-∠ABD= 。(2)变式训练 Ⅰ:如图若∠CBD=30o, ∠ABC=90o,你能求出哪些角的度数? Ⅱ:若在Ⅰ的条件下再添上BP平分∠ABD,你还能求出哪些角的度数? 例2、∠ABC∠PBC∠ABC∠PBC1. 根据图形填空:
①∠AOB=∠AOC+∠ ;
②∠AOD=∠AOB—∠ =∠ —∠COD;
③∠AOC+∠BOD—∠AOB= .BOCBODAOC∠COD 练习2. 如图,∠ABC=60°,∠ABD=145°,BE平分∠ABC,求∠DBE的度数.解: ∵ ∠ABC=60°,∠ABD=145°∠ABD- ∠ABC= 145°- 60°=85°又∵ BE平分∠ABC∴ ∠CBE= ∠ABC= × 60°= 30° ∠CBD+∠CBE= 85°+ 30°=115°∴ ∠CBD=∴ ∠DBE=利用一副三角板,我们能画出哪些度数的角? 探究活动180 o15 o135 o150 o75 o105 o60 o30 o45 o120 o∠AOB=900 ∠1=40.6°, ∠2=49.4°∠ AOB=1800∠4=128.70 ∠3=51.30先观察下图, ∠1+∠2与Rt∠AOB相等吗?再观察下图,∠3+∠4与∠AOB相等吗?∠1+∠2= 900∠3+∠4= 1800 余角 与 补角 的定义余角:如果两个角的和是直角,那么称这两个角互为余角
补角:如果两个角的和是平角,那么称这两个角互为补角.补角与余角是两个角之间的相互关系。
补角与余角与角的位置无关,只与它的度数有关。互为余角的有: ∠1和∠ 3.1、 如图已知∠1=42°, ∠2=138°, ∠ 3=48°,
问图中有没有互余或互补的角?互为补角的有:∠1和∠ 2解:练习2、如图,点O为直线AB上一点, ∠AOC=Rt ∠,
OD是∠ BOC内的一条射线。
图中哪些角互为余角?
哪些角互为补角?互为余角的有:∠COD和∠ DOB解:互为补角的有:∠AOC和∠ COB, ∠AOD和∠ DOB解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC余角 与 补角 的 性 质 若∠α =∠ β,那么∠α的余角和∠ β的余角有何关系?∠α的补角和∠ β的补角又有何关系?
例3.如图,已知∠AOC= ∠BOD=Rt ∠ ,
指出图中还有哪些角相等,并说明理由。解:∠AOB = ∠COD∵ ∠AOC =∠BOD=Rt ∠∴ ∠AOB =∠DOC∴ ∠AOB +∠BOC=Rt ∠∵ ∠DOC +∠BOC=Rt ∠即∠AOB 与∠DOC 都是∠BOC的余角(同角的余角相等)
例4.已知一个角的补角是这个角的余角的4倍,
求这个角的度数。解:设这个角为x度,则这个角的余角是 度,补角是 度.(90-x)(180-x)由题意,得180-x=4(90-x)解方程,得x=60(度)所以这个角的度数为60°1、判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3
互为余角( )√╳╳练习C 2、要测量两堵墙所成的∠ AOB的度数,但人不能进入围墙,如何测量?5.如图,OA⊥OB,OC⊥OD,且∠ COB=50°,则∠AOD= 。130°3.已知∠α= 60°32′则∠α的余角等于_____ 。
则∠α的补角等于 .29°28′119°28′4. 如果∠α的余角是∠α的2倍,则∠α= .如果∠1的补角是∠1的3倍,则∠1= . 30 °45 °6、如图,OB平分∠COD,∠AOB=90°,∠AOC=125°,求比∠COD的补角小19°3′59″的角的度数。解:∠BOC=∠BOD = ∠BOC =35°∠COD =35°×2 =70°∠COD的补角 =110°∴所求的角 =110°-19°3′59″=90°56′1″。DBCOA∠AOC-∠AOB =125°-90°
=35°7、如图2,点O在直线AB上,OD平分∠ AOC,
OE平分∠COB,
①那么OD与OE的位置关系是 ,
②图中互余角有 对,互补角有 对。图2垂直453.什么是角平分线?课堂小结(一)1.比较角的大小有什么方法?度量法、叠合法2.角分为几类?锐角、直角、钝角、平角、周角从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;课堂小结(二)
2、1平角=______度
3、1直角=______度
4、平角是一条直线吗?
5、周角是一条射线吗?360°180°90°( )( )2、∠A与∠P哪个角较大?怎样比较呢?新课引入1267度56度方法一: 度量法,即用量角器量出角的度数,通过比角的度数来比较角的大小.度数大的角大,度数小的角小;反之,角大度数就大,角小度数就小.方法二: 叠合法1观察下列两图,考虑该如何比较∠1和∠2的大小?1探索新知BACABC(p)Q角的大小比较方法:叠合法
测量法请比较每组图中∠ ABC和∠ DEF的大小. BC和ED重合BC落在∠ DEF 的外部BC落在∠ DEF的内部=>< 请观察下图中的一组角,如果要把他们分类,你将怎样分?你的分类标准是什么呢? 等于90°的角.直角:小于直角的角.大于直角而小于平角的角.锐角:钝角:角的分类平角、周角 角的分类例 1、根据右图解下列问题(1)比较∠AOB、∠AOC
∠AOD、∠AOE的大小(2)找出图中的直角、锐角和钝角解:(1)由右图可以看出:
∠ AOB < ∠ AOC < ∠ AOD < ∠ AOE(2)图中的直角有∠AOC,∠BOD ,∠ COE;锐角有∠ AOB, ∠ BOC ,∠ COD, ∠ DOE;钝角有∠ AOD, ∠ BOE。做一做 在一张透明纸上任意画一个角∠ AOB (如右图),把这张透明纸折叠,使角的两边OA和OB重合,然后把这张纸展开、铺平,画出折痕OC。 ∠ AOC与∠ BOC之间有怎样的大小关系?∠ AOC=∠ BOCOABC 从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线.如果给你任意一个角∠AOB,
你有什么方法画出它的角平分线?AOB想一想 你会用量角器画一个角的平分线? 先用量角器量出这个角的大小,再以这个角的顶点为顶点, 一边为始边,在角的内部画一条线,使它与始边所成的角的大小是原角的一半,这条射线就是这个角的平分线。(1)海洋世界在大门的正东方向,你能说出它在大门的北偏东多少度吗?(2)在图中连接各个景点与大门,并用适当的方式表示各角。(3)上面这些角中,哪些是锐角、直角、钝角,并比较它们的大小?学以致用在大门的北偏东900∠BOD, ∠BOA, ∠BOC, ∠DOA, ∠DOC, ∠AOC∠BOC锐角:∠BOD, ∠DOA ∠AOC.∠BOA,∠DOC直角钝角.(4)你能比较出这些角的大小吗? (1)根据图形填空:①∠DBA=∠DBC+ ;②∠DBC=∠DBP- =∠DBA- ;③∠DBP+∠ABC-∠ABD= 。(2)变式训练 Ⅰ:如图若∠CBD=30o, ∠ABC=90o,你能求出哪些角的度数? Ⅱ:若在Ⅰ的条件下再添上BP平分∠ABD,你还能求出哪些角的度数? 例2、∠ABC∠PBC∠ABC∠PBC1. 根据图形填空:
①∠AOB=∠AOC+∠ ;
②∠AOD=∠AOB—∠ =∠ —∠COD;
③∠AOC+∠BOD—∠AOB= .BOCBODAOC∠COD 练习2. 如图,∠ABC=60°,∠ABD=145°,BE平分∠ABC,求∠DBE的度数.解: ∵ ∠ABC=60°,∠ABD=145°∠ABD- ∠ABC= 145°- 60°=85°又∵ BE平分∠ABC∴ ∠CBE= ∠ABC= × 60°= 30° ∠CBD+∠CBE= 85°+ 30°=115°∴ ∠CBD=∴ ∠DBE=利用一副三角板,我们能画出哪些度数的角? 探究活动180 o15 o135 o150 o75 o105 o60 o30 o45 o120 o∠AOB=900 ∠1=40.6°, ∠2=49.4°∠ AOB=1800∠4=128.70 ∠3=51.30先观察下图, ∠1+∠2与Rt∠AOB相等吗?再观察下图,∠3+∠4与∠AOB相等吗?∠1+∠2= 900∠3+∠4= 1800 余角 与 补角 的定义余角:如果两个角的和是直角,那么称这两个角互为余角
补角:如果两个角的和是平角,那么称这两个角互为补角.补角与余角是两个角之间的相互关系。
补角与余角与角的位置无关,只与它的度数有关。互为余角的有: ∠1和∠ 3.1、 如图已知∠1=42°, ∠2=138°, ∠ 3=48°,
问图中有没有互余或互补的角?互为补角的有:∠1和∠ 2解:练习2、如图,点O为直线AB上一点, ∠AOC=Rt ∠,
OD是∠ BOC内的一条射线。
图中哪些角互为余角?
哪些角互为补角?互为余角的有:∠COD和∠ DOB解:互为补角的有:∠AOC和∠ COB, ∠AOD和∠ DOB解:∠BOC=∠AOB -∠AOC
=90°- ∠AOC∠AOD= ∠AOB -∠BOD
=90°- ∠AOC余角 与 补角 的 性 质 若∠α =∠ β,那么∠α的余角和∠ β的余角有何关系?∠α的补角和∠ β的补角又有何关系?
例3.如图,已知∠AOC= ∠BOD=Rt ∠ ,
指出图中还有哪些角相等,并说明理由。解:∠AOB = ∠COD∵ ∠AOC =∠BOD=Rt ∠∴ ∠AOB =∠DOC∴ ∠AOB +∠BOC=Rt ∠∵ ∠DOC +∠BOC=Rt ∠即∠AOB 与∠DOC 都是∠BOC的余角(同角的余角相等)
例4.已知一个角的补角是这个角的余角的4倍,
求这个角的度数。解:设这个角为x度,则这个角的余角是 度,补角是 度.(90-x)(180-x)由题意,得180-x=4(90-x)解方程,得x=60(度)所以这个角的度数为60°1、判断:
①一个角的余角一定是锐角( )
②一个角的补角一定是钝角( )
③若∠1+∠2+∠3=90°,那么∠1、∠2、∠3
互为余角( )√╳╳练习C 2、要测量两堵墙所成的∠ AOB的度数,但人不能进入围墙,如何测量?5.如图,OA⊥OB,OC⊥OD,且∠ COB=50°,则∠AOD= 。130°3.已知∠α= 60°32′则∠α的余角等于_____ 。
则∠α的补角等于 .29°28′119°28′4. 如果∠α的余角是∠α的2倍,则∠α= .如果∠1的补角是∠1的3倍,则∠1= . 30 °45 °6、如图,OB平分∠COD,∠AOB=90°,∠AOC=125°,求比∠COD的补角小19°3′59″的角的度数。解:∠BOC=∠BOD = ∠BOC =35°∠COD =35°×2 =70°∠COD的补角 =110°∴所求的角 =110°-19°3′59″=90°56′1″。DBCOA∠AOC-∠AOB =125°-90°
=35°7、如图2,点O在直线AB上,OD平分∠ AOC,
OE平分∠COB,
①那么OD与OE的位置关系是 ,
②图中互余角有 对,互补角有 对。图2垂直453.什么是角平分线?课堂小结(一)1.比较角的大小有什么方法?度量法、叠合法2.角分为几类?锐角、直角、钝角、平角、周角从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线(1) 和为直角的两个角称互为余角;
(2) 和为平角的两个角称互为补角;(1) 同角或等角的余角相等;
(2) 同角或等角的补角相等;课堂小结(二)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
