16.2.2 二次根式的除法 课件(共15张PPT)
文档属性
| 名称 | 16.2.2 二次根式的除法 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 19:01:52 | ||
图片预览




文档简介
(共15张PPT)
第十六章 二次根式
16.3二次根式的加减
第1课时 二次根式的加减
理解同类二次根式,并能判定哪些是同类二次根式;
核心素养目标:
理解和掌握二次根式加减的方法;
先提出问题,分析问题,在分析问题中,渗透对二次根式进行加减的方法的理解.再总结经验,用它来指导根式的计算和化简.
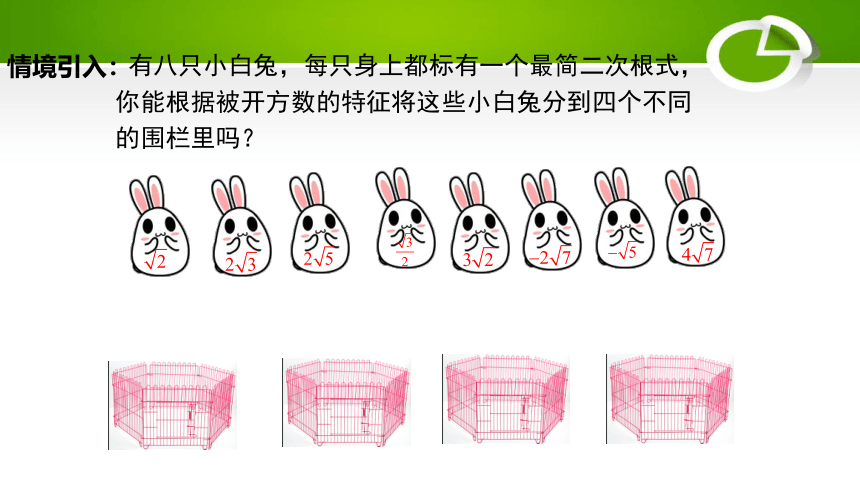
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的围栏里吗?
情境引入:
问题1.满足什么条件的根式是最简二次根式
试化简下列二次根式:
问题2.上述化简后的二次根式有什么特点 你会怎么对它们进行分类
几个二次根式化简后被开方数相同
为一组;
为一组.
交流预习:
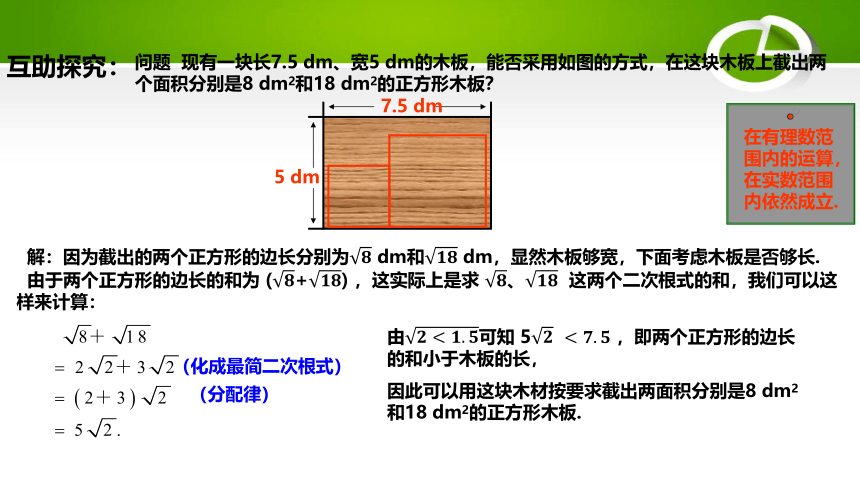
解:因为截出的两个正方形的边长分别为 dm和 dm,显然木板够宽,下面考虑木板是否够长.
问题 现有一块长7.5 dm、宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
由于两个正方形的边长的和为 (+) ,这实际上是求 、 这两个二次根式的和,我们可以这样来计算:
7.5 dm
5 dm
(化成最简二次根式)
(分配律)
在有理数范围内的运算,在实数范围内依然成立.
互助探究:
由可知 5 ,即两个正方形的边长的和小于木板的长,
因此可以用这块木材按要求截出两面积分别是8 dm2和18 dm2的正方形木板.
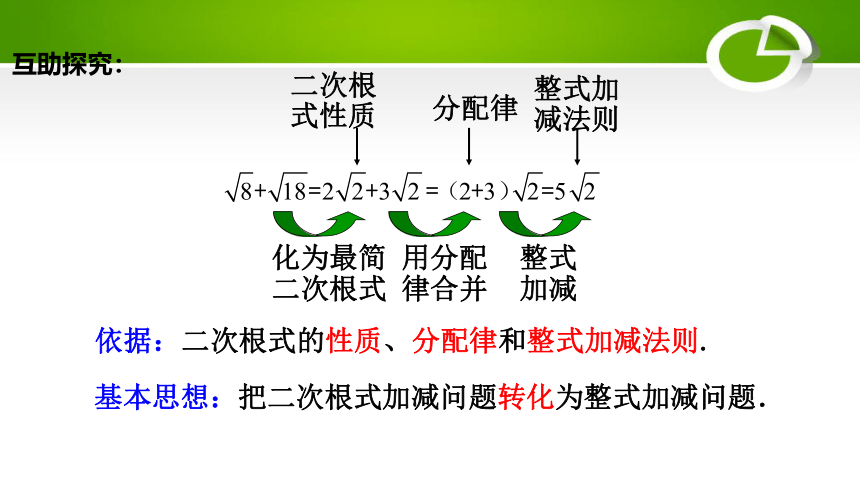
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
互助探究:
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例1 计算:
(1)
.
解:(1)
例题精讲:
例2 计算
解:
解:原式
例题精讲:
教材13页练习1
下列计算是否正确?为什么?
不正确
不正确
正确
跟踪练习:
教材13页练习2
计算:
(1)
(2)
.
(3)
(4)
跟踪练习:
如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
解:
答:圆环的宽度d为 cm.
R-r
跟踪练习:
教材13页练习3
二次根式加减
法则
注意
运算顺序
运算原理
一化简二判断三合并
运算律仍然适用
与实数的运算顺序一样
课堂小结:
1.二次根式: 中,与 能进行合并的是( )
A.
B .
C .
D .
2.下列运算中错误的是( )
A.
B.
C.
D.
A
C
课堂检测:
课后作业:
必做题:教科书第13页练习2,3;
选做题:习题16.3第1,2,3题.
第十六章 二次根式
16.3二次根式的加减
第1课时 二次根式的加减
理解同类二次根式,并能判定哪些是同类二次根式;
核心素养目标:
理解和掌握二次根式加减的方法;
先提出问题,分析问题,在分析问题中,渗透对二次根式进行加减的方法的理解.再总结经验,用它来指导根式的计算和化简.
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的围栏里吗?
情境引入:
问题1.满足什么条件的根式是最简二次根式
试化简下列二次根式:
问题2.上述化简后的二次根式有什么特点 你会怎么对它们进行分类
几个二次根式化简后被开方数相同
为一组;
为一组.
交流预习:
解:因为截出的两个正方形的边长分别为 dm和 dm,显然木板够宽,下面考虑木板是否够长.
问题 现有一块长7.5 dm、宽5 dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8 dm2和18 dm2的正方形木板?
由于两个正方形的边长的和为 (+) ,这实际上是求 、 这两个二次根式的和,我们可以这样来计算:
7.5 dm
5 dm
(化成最简二次根式)
(分配律)
在有理数范围内的运算,在实数范围内依然成立.
互助探究:
由可知 5 ,即两个正方形的边长的和小于木板的长,
因此可以用这块木材按要求截出两面积分别是8 dm2和18 dm2的正方形木板.
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
互助探究:
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例1 计算:
(1)
.
解:(1)
例题精讲:
例2 计算
解:
解:原式
例题精讲:
教材13页练习1
下列计算是否正确?为什么?
不正确
不正确
正确
跟踪练习:
教材13页练习2
计算:
(1)
(2)
.
(3)
(4)
跟踪练习:
如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
解:
答:圆环的宽度d为 cm.
R-r
跟踪练习:
教材13页练习3
二次根式加减
法则
注意
运算顺序
运算原理
一化简二判断三合并
运算律仍然适用
与实数的运算顺序一样
课堂小结:
1.二次根式: 中,与 能进行合并的是( )
A.
B .
C .
D .
2.下列运算中错误的是( )
A.
B.
C.
D.
A
C
课堂检测:
课后作业:
必做题:教科书第13页练习2,3;
选做题:习题16.3第1,2,3题.
