3.1 一元一次方程及其解法 (1) 课件(共28张PPT)
文档属性
| 名称 | 3.1 一元一次方程及其解法 (1) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1003.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 14:38:27 | ||
图片预览








文档简介
(共28张PPT)
沪科版 七年级上册
3.1 一元一次方程及其解法 (1)
教学目标
1.知道等式的基本性质,掌握利用等式的基本性质解一元一次方程;
2.学会写一元一次方程的检验,理解解一元一次方程过程中的转化思想;
3.通过解一元一次方程体验探索成功的乐趣。
教学重点:利用等式的基本性质解简单的一元一次方程。
教学难点:理解解一元一次方程的实质是对等式的变形,变形的目的是将原方程变形为x=a(其中a为常数)的形式.
给出的下列式子的名称:
含有未知数的等式叫做方程.
2x-5,
2x,
2x-5=7,
2x+5=-1.
单项式
多项式
方程
方程
学习新知
(1) 在参加2008年北京奥运会的中国代表队中,羽毛球运动员有19人,比跳水运动员的2倍少1人.参加奥运会的跳水运动员有多少人?
解:
设参加奥运会的跳水运动员有x人.
根据题意,
得
2x
-1
=19
跳水运动员的2倍少1人=羽毛球运动员有19人
(2) 王玲今年12岁,她爸爸36岁,问再过几年,她爸爸年龄是她年龄的2倍?
解:
设再过x年,王玲的年龄是 岁,她爸爸的年龄为 .
根据题意,
得
36+x
(12+x)
(36+x)
(12+x)
=2
王玲爸爸的年龄=王玲年龄的2倍
只含有一个未知数(元),未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程.
观察所列的方程,每个方程有几个未知数,未知数的指数是多少?
2x-1=19
36+x
=2(12+x)
一.判断下列式子是不是方程,是打”√”不是打”X”:
(1) 1+2=3 ( ) (4) ( )
(2) 1+2x=4 ( ) (5) x+y=2 ( )
(3) x+1-3 ( ) (6) x2-1=0 ( )
x
x
x
√
√
√
x+2﹥1
练习巩固
当 x = 5 时,
+
1700
=2450
150x
对于方程
左边= 1700+150×5 =2 450,
右边=2450
所以 左边=右边,
所以 x = 5 是这个方程的解.
当x = 4 时,
右边=2450
所以 左边≠右边,
所以 x=4不是这个方程的解.
左边= 1700+150×4 =2 300,
使方程等号左右两边相等的未知数的值,叫做方程的解.
一元方程的解也叫做方程的根.
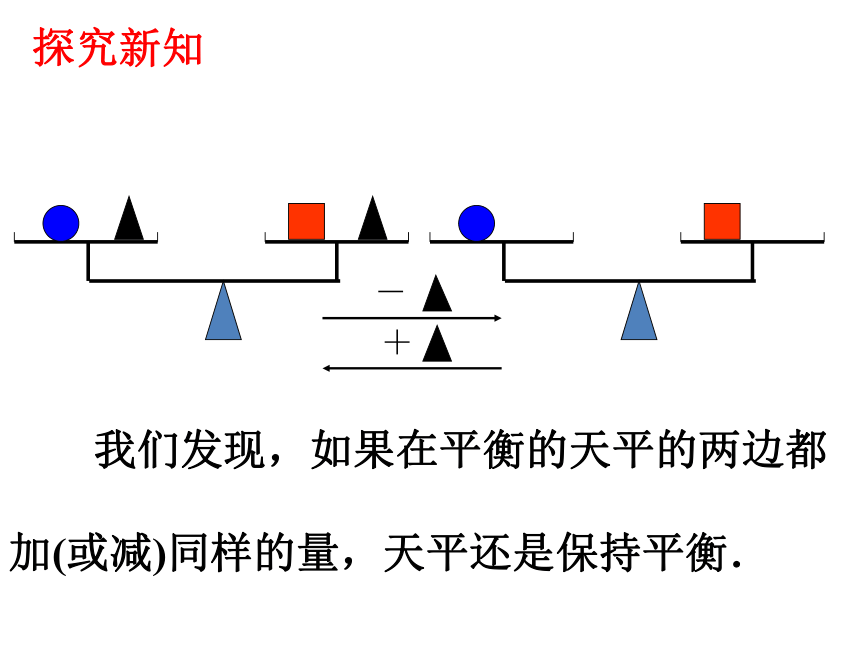
我们发现,如果在平衡的天平的两边都加(或减)同样的量,天平还是保持平衡.
-
+
探究新知
如果 a = b,那么 a = b
等式的性质1
等式两边加(或减)同一个数(或式子),
结果仍相等.
± c
± c
用式子的形式怎样表示
我们发现,如果在天平的两边都乘以(或除以)不为0的同样的量,天平还保持平衡.
÷
×
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 a = b,那么ac =
如果 a = b,那么 (c≠ 0).
等式的性质2
bc
a
c
b
c
=
用式子的形式怎样表示
等式的基本性质3
如果a=b,那么b=a.
等式的基本性质4
如果a=b,b=c,那么a=c.
根据这一性质,在解题过程中一个量用与它相等的量来代替,简称等量代换.
(对称性)
(传递性)
在下面的括号内填上适当的数或者式子:
(1)因为x-5=4
所以x-5+5=4+( )
(2)因为2x=x-5
所以2x+( ) =x-5-3x
(3)因为-3x+8=6-x
所以-3x+( )+8-8= 6+x-x-8
5
-3x
x
练习巩固
1.说明下列变形是根据等式哪一条基本性质得到的
(1)如果5x+3=7,那么5x=4
(2)如果-8x=4,那么x=-0.5
(3)如果-5a=-5b,那么a=b
等式基本性质1,
等式基本性质2 ,
等式基本性质2 ,
两边同减去3.
两边同除以-8.
两边同除以-5.
(4)如果3x=2x+1,那么x=1;
(5)如果-0.25=x,那么x=-0.25;
(6)如果x=y,y=z ,那么x=z.
等式基本性质4
等式基本性质3
等式基本性质1,
两边同减去2x
1.说明下列变形是根据等式哪一条基本性质得到的
例1.解方程:2x-1=19.
解: 方程两边同时加上1,得
2x-1+1=19+1
即 2x=20
两边都除以2,得
x=10
检验:把x=10分别代入原方程的两边,得
左边=2×10-1=19,
即 左边=右边.
所以 x=10是原方程的解.
(等式基本性质1)
(等式基本性质2)
右边=19,
例题解析
练习:根据等式的性质解下列方程,并检验:
(1) 5x-7=8;
(1)两边加 7,得
5x-7+7=8+7;
化简,得:
5x=15;
两边同时除以5,得
x = 3.
检验:
当x=3时,
左边=5 × 3-7 = 8,
方程的右边 = 8,
所以左边=右边,
所以x=3是方程的解.
练习:根据等式的性质解下列方程,并检验:
(2) 27=7+4x;
(2)两边减7,得
27-7=7+4x-7;
化简,得:
20=4x;
两边同时除以4,得
5 = x.
检验:
当x=5时,
左边=27,
右边 =7+4×5=27 ,
所以左边=右边,
所以x=5是方程的解.
即 x=5
练习:根据等式的性质解下列方程,并检验:
(3) = x- ;
(3)两边加 ,得
+ = x - + ;
化简,得:
= x;
两边同时乘以3,得
2= x.
检验:
当x=2时,
所以左边=右边,
所以x=2是方程的解.
1
2
1
6
1
3
1
6
1
2
1
6
1
6
1
6
1
3
2
3
1
3
左边= ,
右边 = ×2- = ,
1
2
1
2
1
6
1
3
即 x=2
归纳总结:
2.解一元一次方程的实质就是:
——利用等式的性质求出未知数的值.
——将方程化为“x=a (a为常数)”的形式.
1.等式的基本性质;
① 如果 a = b,那么 a ± c = b ± c
② 如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
a
c
b
c
=
2.已知 x = y,下列变形中不一定正确的是( ).
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
x
c2
y
c2
=
选择题
1.下列各式中,是方程的是( ).
A. x + 3 B. x - 2 > 0
C. 2x + 7 = 3 D. 2 + 3 = 5
巩固提高
C
D
2
3.在下列方程中一元一次方程的个数有( )
(1)3x+5=12; (2) + =5;
(3)2x+y=3; (4) =2.
x-3
x
x
2
x+1
3
4.已知方程3x2m-1-3=0是关于x的一元一次方程,
则m的值是( )
A.1个 B.2个 C.3个 D.4个
A.0 B.1 C.-1 D.0或-1
B
B
3.写一个解为 x=-2的一元一次方程: .
2. 若3x4n-7+5 =0 是一元一次方程,则n= .
4.方程x+8=4的解是 .
1.若a+2b = x+10,则2a+2b = x+10+ .
填空题
巩固提高
a
2
x=-2
x+2=0
6.已知关于x的方程3x-2m=4的解是x=m,则m
的值是___.
7.已知方程︱x︱=2,那么方程的解是 .
5.若x=-3是方程x+a=4的解,则a的值是 .
7
4
x=2
或x=-2
今天作业
课本P91第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
3.1 一元一次方程及其解法 (1)
教学目标
1.知道等式的基本性质,掌握利用等式的基本性质解一元一次方程;
2.学会写一元一次方程的检验,理解解一元一次方程过程中的转化思想;
3.通过解一元一次方程体验探索成功的乐趣。
教学重点:利用等式的基本性质解简单的一元一次方程。
教学难点:理解解一元一次方程的实质是对等式的变形,变形的目的是将原方程变形为x=a(其中a为常数)的形式.
给出的下列式子的名称:
含有未知数的等式叫做方程.
2x-5,
2x,
2x-5=7,
2x+5=-1.
单项式
多项式
方程
方程
学习新知
(1) 在参加2008年北京奥运会的中国代表队中,羽毛球运动员有19人,比跳水运动员的2倍少1人.参加奥运会的跳水运动员有多少人?
解:
设参加奥运会的跳水运动员有x人.
根据题意,
得
2x
-1
=19
跳水运动员的2倍少1人=羽毛球运动员有19人
(2) 王玲今年12岁,她爸爸36岁,问再过几年,她爸爸年龄是她年龄的2倍?
解:
设再过x年,王玲的年龄是 岁,她爸爸的年龄为 .
根据题意,
得
36+x
(12+x)
(36+x)
(12+x)
=2
王玲爸爸的年龄=王玲年龄的2倍
只含有一个未知数(元),未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程.
观察所列的方程,每个方程有几个未知数,未知数的指数是多少?
2x-1=19
36+x
=2(12+x)
一.判断下列式子是不是方程,是打”√”不是打”X”:
(1) 1+2=3 ( ) (4) ( )
(2) 1+2x=4 ( ) (5) x+y=2 ( )
(3) x+1-3 ( ) (6) x2-1=0 ( )
x
x
x
√
√
√
x+2﹥1
练习巩固
当 x = 5 时,
+
1700
=2450
150x
对于方程
左边= 1700+150×5 =2 450,
右边=2450
所以 左边=右边,
所以 x = 5 是这个方程的解.
当x = 4 时,
右边=2450
所以 左边≠右边,
所以 x=4不是这个方程的解.
左边= 1700+150×4 =2 300,
使方程等号左右两边相等的未知数的值,叫做方程的解.
一元方程的解也叫做方程的根.
我们发现,如果在平衡的天平的两边都加(或减)同样的量,天平还是保持平衡.
-
+
探究新知
如果 a = b,那么 a = b
等式的性质1
等式两边加(或减)同一个数(或式子),
结果仍相等.
± c
± c
用式子的形式怎样表示
我们发现,如果在天平的两边都乘以(或除以)不为0的同样的量,天平还保持平衡.
÷
×
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 a = b,那么ac =
如果 a = b,那么 (c≠ 0).
等式的性质2
bc
a
c
b
c
=
用式子的形式怎样表示
等式的基本性质3
如果a=b,那么b=a.
等式的基本性质4
如果a=b,b=c,那么a=c.
根据这一性质,在解题过程中一个量用与它相等的量来代替,简称等量代换.
(对称性)
(传递性)
在下面的括号内填上适当的数或者式子:
(1)因为x-5=4
所以x-5+5=4+( )
(2)因为2x=x-5
所以2x+( ) =x-5-3x
(3)因为-3x+8=6-x
所以-3x+( )+8-8= 6+x-x-8
5
-3x
x
练习巩固
1.说明下列变形是根据等式哪一条基本性质得到的
(1)如果5x+3=7,那么5x=4
(2)如果-8x=4,那么x=-0.5
(3)如果-5a=-5b,那么a=b
等式基本性质1,
等式基本性质2 ,
等式基本性质2 ,
两边同减去3.
两边同除以-8.
两边同除以-5.
(4)如果3x=2x+1,那么x=1;
(5)如果-0.25=x,那么x=-0.25;
(6)如果x=y,y=z ,那么x=z.
等式基本性质4
等式基本性质3
等式基本性质1,
两边同减去2x
1.说明下列变形是根据等式哪一条基本性质得到的
例1.解方程:2x-1=19.
解: 方程两边同时加上1,得
2x-1+1=19+1
即 2x=20
两边都除以2,得
x=10
检验:把x=10分别代入原方程的两边,得
左边=2×10-1=19,
即 左边=右边.
所以 x=10是原方程的解.
(等式基本性质1)
(等式基本性质2)
右边=19,
例题解析
练习:根据等式的性质解下列方程,并检验:
(1) 5x-7=8;
(1)两边加 7,得
5x-7+7=8+7;
化简,得:
5x=15;
两边同时除以5,得
x = 3.
检验:
当x=3时,
左边=5 × 3-7 = 8,
方程的右边 = 8,
所以左边=右边,
所以x=3是方程的解.
练习:根据等式的性质解下列方程,并检验:
(2) 27=7+4x;
(2)两边减7,得
27-7=7+4x-7;
化简,得:
20=4x;
两边同时除以4,得
5 = x.
检验:
当x=5时,
左边=27,
右边 =7+4×5=27 ,
所以左边=右边,
所以x=5是方程的解.
即 x=5
练习:根据等式的性质解下列方程,并检验:
(3) = x- ;
(3)两边加 ,得
+ = x - + ;
化简,得:
= x;
两边同时乘以3,得
2= x.
检验:
当x=2时,
所以左边=右边,
所以x=2是方程的解.
1
2
1
6
1
3
1
6
1
2
1
6
1
6
1
6
1
3
2
3
1
3
左边= ,
右边 = ×2- = ,
1
2
1
2
1
6
1
3
即 x=2
归纳总结:
2.解一元一次方程的实质就是:
——利用等式的性质求出未知数的值.
——将方程化为“x=a (a为常数)”的形式.
1.等式的基本性质;
① 如果 a = b,那么 a ± c = b ± c
② 如果 a = b,那么 a c = b c
如果 a = b,那么 (c≠ 0)
a
c
b
c
=
2.已知 x = y,下列变形中不一定正确的是( ).
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
x
c2
y
c2
=
选择题
1.下列各式中,是方程的是( ).
A. x + 3 B. x - 2 > 0
C. 2x + 7 = 3 D. 2 + 3 = 5
巩固提高
C
D
2
3.在下列方程中一元一次方程的个数有( )
(1)3x+5=12; (2) + =5;
(3)2x+y=3; (4) =2.
x-3
x
x
2
x+1
3
4.已知方程3x2m-1-3=0是关于x的一元一次方程,
则m的值是( )
A.1个 B.2个 C.3个 D.4个
A.0 B.1 C.-1 D.0或-1
B
B
3.写一个解为 x=-2的一元一次方程: .
2. 若3x4n-7+5 =0 是一元一次方程,则n= .
4.方程x+8=4的解是 .
1.若a+2b = x+10,则2a+2b = x+10+ .
填空题
巩固提高
a
2
x=-2
x+2=0
6.已知关于x的方程3x-2m=4的解是x=m,则m
的值是___.
7.已知方程︱x︱=2,那么方程的解是 .
5.若x=-3是方程x+a=4的解,则a的值是 .
7
4
x=2
或x=-2
今天作业
课本P91第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
