3.1 一元一次方程及其解法 (5) 课件(共23张PPT)
文档属性
| 名称 | 3.1 一元一次方程及其解法 (5) 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 961.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 14:40:32 | ||
图片预览








文档简介
(共23张PPT)
沪科版 七年级上册
3.1 一元一次方程及其解法 (5)
教学目标
加深对一元一次方程及其相关概念的理解;理解解一元一次方程的一般步骤,熟练地解一元一次方程;以方程为工具,分析、解决实际问题. 体会列方程中蕴涵的 “数学建模思想”和解方程中蕴涵的“化归思想”;会一元一次方程的简单应用。
教学重点:一元一次方程的解法
教学难点:熟练地解一元一次方
变形名称
去分母
去括号
移项
系数化为1
防止漏乘,注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了.
合并同类项
解含有分母的一元一次方程的步骤:
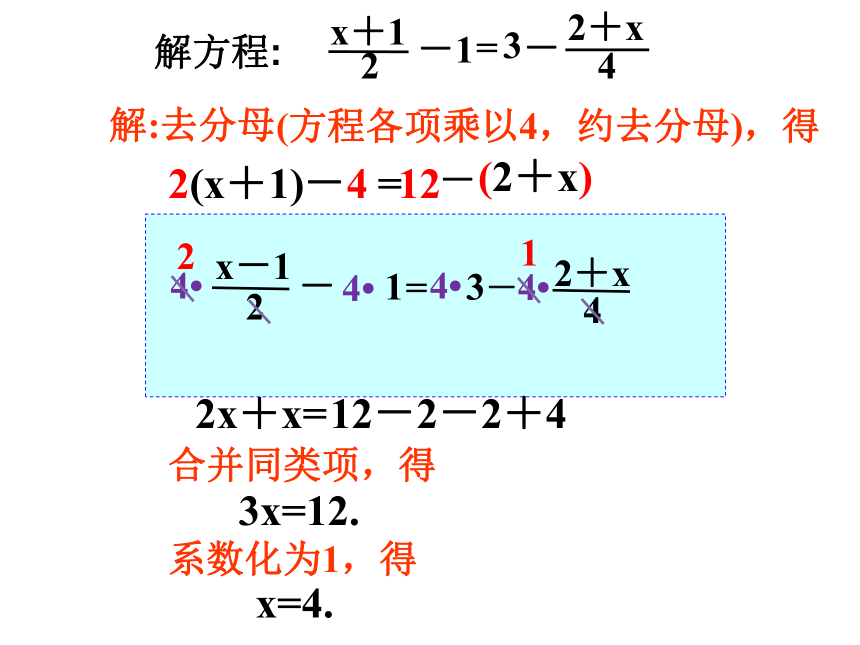
复习旧知
=
12
-2-x
4
2+x
-
2
x+1
=
3
解方程:
-1
解:去分母
合并同类项,得
移项,得
2(x+1)
系数化为1,得
去括号,得
2x+x=
3x=12.
x=4.
2x+2-4
(方程各项乘以4,约去分母),得
2
3-
4
-
2+x
x-1
1
=
4
4
4
4
2
1
(2+x)
-4
=
12
-
12-2-2+4
(1)什么叫做方程?请你举出一个例子.
(2)什么叫做方程的解?
使方程等号左右两边相等的未知数的值,
叫做方程的解.
含有未知数的等式叫做方程.
(3)什么叫做一元一次方程?
请你举出一个一元一次方程的例子.
只含有一个未知数,未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程.
1.若a=b,则a±c=b±c.
2.若a=b,则ac=bc, .
3.对称性:如果a=b,那么b=a.
4.传递性:如果a=b,b=c,那么a=c.
等式的基本性质:
(4)等式的基本性质是什么?
a
c
b
c
=
(c≠ 0)
1.下列各式中,是方程的是( )
A.x + 3 B.x -2 > 0
C.2x+7 = 3 D.2 + 3 = 5
c
练习一
C
c
2
1
2.在下列方程中哪些是一元一次方程
(1)3x+5=12;
(2) + =5;
(3)2x+y=3;
(4)y2+5y-6=0;
(5) = 2.
x+1
3
9
2
x-3
x
√
√
3.写一个解为 x=-2的一元一次方程: .
4. 若3x4n-7+5是一元一次方程,则n= ;
x+2=0
2
6.若x=-3是方程x+a=4的解,则a= .
5.方程x+8=4的解是 .
7
x= - 4
4n-7=
1
1. 判断,下列方程的变形是否正确?
(1)由3+x=5,得x=5+3;
( )
( )
( )
( )
×
×
×
√
练习二
(2)由7x=-4,得x=- ;
(3)由 y=0,得y=2;
(4)由3=x+2,得x=3-2.
7
4
1
2
如果a=b,那么b=a.
2.若a+2b = x+10,则2a+2b = x+10+ .
a
D
3.已知x = y,下列变形中不一定正确的是( )
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
x
c2
y
c2
=
(c≠ 0)
4.解方程:
0.5
x-3
-
0.2
x+4
=1.6
解:
整理,得
5
10x-30
-
2
10x+40
=1.6
去分母,得
2 (10x-30)
-
5 (10x+40)
=16
去括号,得
20x-60
-
50x-200
=16
移项,得
20x-50x
=
16
+60
+200
合并同类项,得
-30x
=276
系数化为1,得
x=-9.2.
4.解方程:
0.5
x-3
-
0.2
x+4
=1.6
解:
整理,得
2 (x-3)
-
5 (x+4)
=1.6
去括号,得
2x-6
-
5x-20
=1.6
移项,得
2x-5x
=
1.6
+6
+20
合并同类项,得
-3x
=27.6
系数化为1,得
x=-9.2.
5.在公式 v=v0+at 中,已知v=100,v0=25,
a=10,求t.
解:把v=100,v0=25, a=10代入v=v0+at,得
100=25+10t
-10t =25-100
-10t =-75
t = 7.5
练习三
6.在公式 S=2πr(r+h)中,已知S=942,r=10,
求h(π取3.14).
解:把S=942, r=10代入S=2πr(r+h),得
942=2×3.14×(10+h )
150=10+h
-h =10-150
h = 140
-h =-140
7. 已知x=5是方程ax-8=20+a的解,求系数a.
解:把x=5, 代入ax-8=20+a,得
5a-8=20+a
5a-a=20+8
4a=28
a = 7
1.依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
去分母,得3(3x+5)=2(2x-1). ( )
去括号,得9x+15=4x-2. ( )
( ),得9x-4x=-15-2. ( )
合并同类项,得5x=-17.
( ),得 ( )
巩固提高
分数的基本性质
等式性质2
去括号的法则
移项
等式性质1
等式性质2
未知数系数化为1
(1) 3[2x-1-3(2x-1)]=5.
2. 解下列方程:
(2) x- =2- .
x-1
2
3
x+2
解:(1)
3[2x-1-6x+3]=5
3[-4x+2]=5
-12x+6=5
-12x=-1
x=
12
1
(2) 6x-2(x+2)
=12-3(x-1)
6x-2x-4=
12-3x+3
4x-4=
15-3x
7x=19
x=
7
19
3.解方程:
x+2( x+1 )= 8+x
1
2
5
4
解:
x+ x+2 = 8+x
1
2
5
2
3x+2 = 8+x
2x= 6
x = 3
今天作业
课本P126第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 七年级上册
3.1 一元一次方程及其解法 (5)
教学目标
加深对一元一次方程及其相关概念的理解;理解解一元一次方程的一般步骤,熟练地解一元一次方程;以方程为工具,分析、解决实际问题. 体会列方程中蕴涵的 “数学建模思想”和解方程中蕴涵的“化归思想”;会一元一次方程的简单应用。
教学重点:一元一次方程的解法
教学难点:熟练地解一元一次方
变形名称
去分母
去括号
移项
系数化为1
防止漏乘,注意添括号;
注意符号,防止漏乘;
移项要变号,防止漏项;
系数为1或-1时,记得省略1;
分子、分母不要写倒了.
合并同类项
解含有分母的一元一次方程的步骤:
复习旧知
=
12
-2-x
4
2+x
-
2
x+1
=
3
解方程:
-1
解:去分母
合并同类项,得
移项,得
2(x+1)
系数化为1,得
去括号,得
2x+x=
3x=12.
x=4.
2x+2-4
(方程各项乘以4,约去分母),得
2
3-
4
-
2+x
x-1
1
=
4
4
4
4
2
1
(2+x)
-4
=
12
-
12-2-2+4
(1)什么叫做方程?请你举出一个例子.
(2)什么叫做方程的解?
使方程等号左右两边相等的未知数的值,
叫做方程的解.
含有未知数的等式叫做方程.
(3)什么叫做一元一次方程?
请你举出一个一元一次方程的例子.
只含有一个未知数,未知数的次数都是1,且等式两边都是整式的方程叫做一元一次方程.
1.若a=b,则a±c=b±c.
2.若a=b,则ac=bc, .
3.对称性:如果a=b,那么b=a.
4.传递性:如果a=b,b=c,那么a=c.
等式的基本性质:
(4)等式的基本性质是什么?
a
c
b
c
=
(c≠ 0)
1.下列各式中,是方程的是( )
A.x + 3 B.x -2 > 0
C.2x+7 = 3 D.2 + 3 = 5
c
练习一
C
c
2
1
2.在下列方程中哪些是一元一次方程
(1)3x+5=12;
(2) + =5;
(3)2x+y=3;
(4)y2+5y-6=0;
(5) = 2.
x+1
3
9
2
x-3
x
√
√
3.写一个解为 x=-2的一元一次方程: .
4. 若3x4n-7+5是一元一次方程,则n= ;
x+2=0
2
6.若x=-3是方程x+a=4的解,则a= .
5.方程x+8=4的解是 .
7
x= - 4
4n-7=
1
1. 判断,下列方程的变形是否正确?
(1)由3+x=5,得x=5+3;
( )
( )
( )
( )
×
×
×
√
练习二
(2)由7x=-4,得x=- ;
(3)由 y=0,得y=2;
(4)由3=x+2,得x=3-2.
7
4
1
2
如果a=b,那么b=a.
2.若a+2b = x+10,则2a+2b = x+10+ .
a
D
3.已知x = y,下列变形中不一定正确的是( )
A.x-5=y-5 B.-3x=-3y
C.mx=my D.
x
c2
y
c2
=
(c≠ 0)
4.解方程:
0.5
x-3
-
0.2
x+4
=1.6
解:
整理,得
5
10x-30
-
2
10x+40
=1.6
去分母,得
2 (10x-30)
-
5 (10x+40)
=16
去括号,得
20x-60
-
50x-200
=16
移项,得
20x-50x
=
16
+60
+200
合并同类项,得
-30x
=276
系数化为1,得
x=-9.2.
4.解方程:
0.5
x-3
-
0.2
x+4
=1.6
解:
整理,得
2 (x-3)
-
5 (x+4)
=1.6
去括号,得
2x-6
-
5x-20
=1.6
移项,得
2x-5x
=
1.6
+6
+20
合并同类项,得
-3x
=27.6
系数化为1,得
x=-9.2.
5.在公式 v=v0+at 中,已知v=100,v0=25,
a=10,求t.
解:把v=100,v0=25, a=10代入v=v0+at,得
100=25+10t
-10t =25-100
-10t =-75
t = 7.5
练习三
6.在公式 S=2πr(r+h)中,已知S=942,r=10,
求h(π取3.14).
解:把S=942, r=10代入S=2πr(r+h),得
942=2×3.14×(10+h )
150=10+h
-h =10-150
h = 140
-h =-140
7. 已知x=5是方程ax-8=20+a的解,求系数a.
解:把x=5, 代入ax-8=20+a,得
5a-8=20+a
5a-a=20+8
4a=28
a = 7
1.依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
去分母,得3(3x+5)=2(2x-1). ( )
去括号,得9x+15=4x-2. ( )
( ),得9x-4x=-15-2. ( )
合并同类项,得5x=-17.
( ),得 ( )
巩固提高
分数的基本性质
等式性质2
去括号的法则
移项
等式性质1
等式性质2
未知数系数化为1
(1) 3[2x-1-3(2x-1)]=5.
2. 解下列方程:
(2) x- =2- .
x-1
2
3
x+2
解:(1)
3[2x-1-6x+3]=5
3[-4x+2]=5
-12x+6=5
-12x=-1
x=
12
1
(2) 6x-2(x+2)
=12-3(x-1)
6x-2x-4=
12-3x+3
4x-4=
15-3x
7x=19
x=
7
19
3.解方程:
x+2( x+1 )= 8+x
1
2
5
4
解:
x+ x+2 = 8+x
1
2
5
2
3x+2 = 8+x
2x= 6
x = 3
今天作业
课本P126第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
