【备考2023】浙教版科学中考第一轮复习--物理模块(十四):欧姆定律与电路计算【word,含答案解析】
文档属性
| 名称 | 【备考2023】浙教版科学中考第一轮复习--物理模块(十四):欧姆定律与电路计算【word,含答案解析】 |

|
|
| 格式 | doc | ||
| 文件大小 | 770.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2022-12-12 00:00:00 | ||
图片预览




文档简介
一、欧姆定律
1.探究电流与电压、电阻的关系
控制变量法设计对照实验:
①保持电阻不变,改变电压研究电流随电压的变化关系;
②保持电压不变,改变电阻研究电流随电阻的变化关系。
实验结论:
①在电阻一定的情况下,导体中的电流与加在导体两端的电压成正比;
②在电压一定的情况下,导体中的电流与导体的电阻成反比。
2.欧姆定律的内容:导体中的电流,跟这段导体两端的电压成正比,跟这段导体的电阻成反比。数学表达式:I=U/R
【注意】
1.欧姆定律适用于纯电阻电路。所谓纯电阻电路指用电器工作时,消耗的电能完全转化为内能的电路,含电动机的电路不能直接用欧姆定律计算。
2.I、U、R对应同一导体或同一段电路,不同时刻、不同导体或不同段电路三者不能混用。
3.同一导体(即R一定时),则I与U成正比;同一电源(即U一定时),则I与R成反比,不能说成是R与I成反比。
4.导体的电阻由导体本身的长度、横截面积、材料、温度等因素决定。电阻值可通过欧姆定律变形公式R=U/I计算,R与U和I的比值有关,但R与外加电压U和通过电流I等因素无关,即使电阻两端没有外加电压,内部没有电流通过,电阻依然存在。
二、伏安法测电阻
1.用电压表和电流表分别测出电路中某一导体两端的电压和通过的电流,就可以根据欧姆定律算出这个导体的电阻,这种用电压表和电流表测电阻的方法叫伏安法。
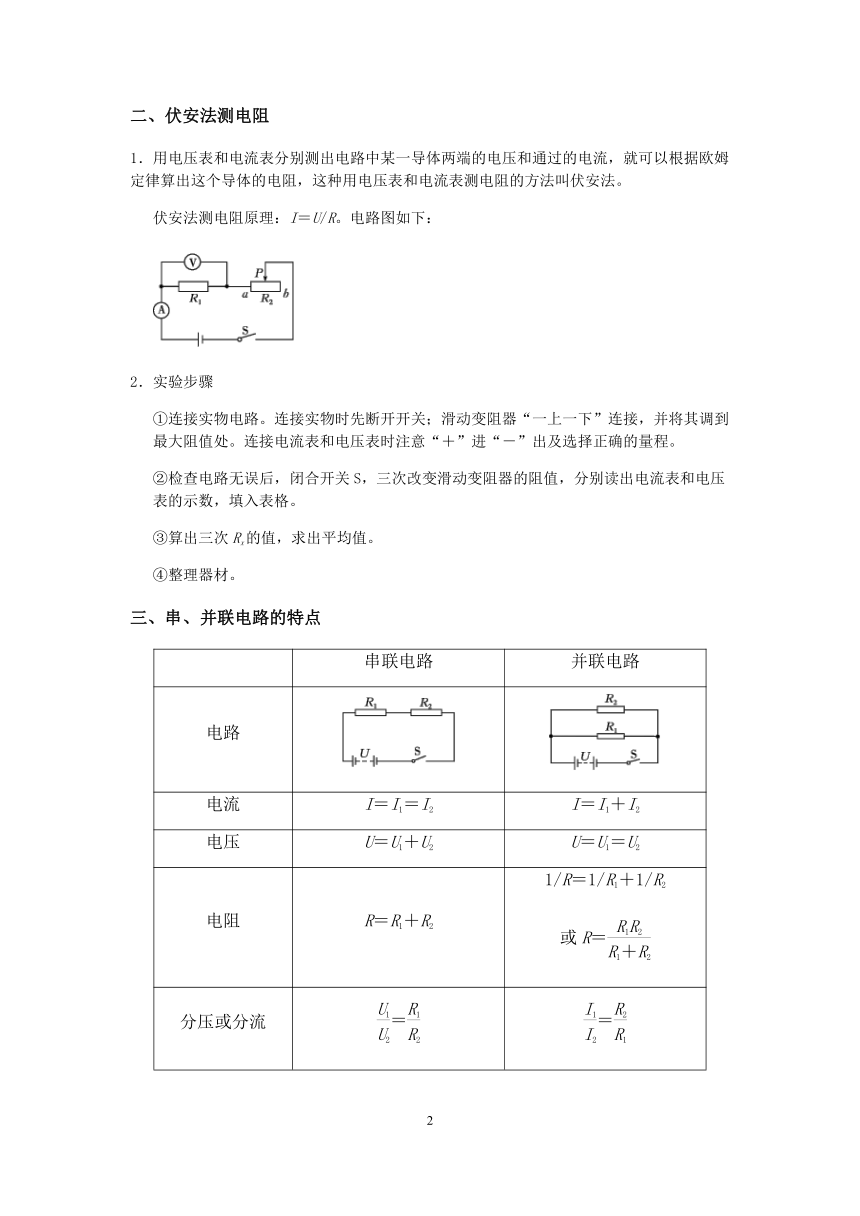
伏安法测电阻原理:I=U/R。电路图如下:
2.实验步骤
①连接实物电路。连接实物时先断开开关;滑动变阻器“一上一下”连接,并将其调到最大阻值处。连接电流表和电压表时注意“+”进“-”出及选择正确的量程。
②检查电路无误后,闭合开关S,三次改变滑动变阻器的阻值,分别读出电流表和电压表的示数,填入表格。
③算出三次Rx的值,求出平均值。
④整理器材。
三、串、并联电路的特点
串联电路 并联电路
电路
电流 I=I1=I2 I=I1+I2
电压 U=U1+U2 U=U1=U2
电阻 R=R1+R2 1/R=1/R1+1/R2或R=
分压或分流 = =
四、欧姆电路动态分析
串联电路中电压与电阻成正比,即=(分压原理),因此串联电路中,电阻越大电压就越大,当其中一个电阻增大时,它两端的电压也会变大,又因为电路总电压不变,所以其他用电器的电压就会变小。并联电路中,电流与电阻成反比,即=(分流原理),因此串联电路中,电阻越大电流就越小。
步 骤:(1)判断用电器的串并联方式(电路较复杂时,电压表=断路;电流表=短路);
(2)弄清电表的测量对象;
(3)认清滑动变阻器滑片的移动或开关开、闭对电路阻值的影响;
(4)利用欧姆定律及其变形公式,结合串联或并联电路的特点进行分析。
【总结】
常规分析方法:局部电阻变化→总电阻变化→总电流变化→局部电流、电压变化(先分析定值电阻的电流、电压的变化,再分析局部电阻变化的那部分电路的变化情况)
简便分析方法:“串反并同”或“大电阻大电压”即测量对象与变阻器串联时,变化与变阻器相同,反之相反。
五、欧姆定律故障分析
串联电路单故障判断方法
并联电路单故障判断方法
注 意:①在复杂电路故障判断时,先列出故障原因,再把电表变化现象列出,寻找合适选项。
②并联电路基本上不考短路故障,只会涉及电压表(测电源)与干路电流;因此重点需要放在串联电路故障分析上,增加总结环节。
总结:常见的电路故障及原因
故障 原因
闭合开关后,灯泡忽明忽暗,两表指针来回摆动 电路某处接触不良
闭合开关前灯泡发光,闭合开关后灯泡不亮了两表也无示数 开关与电源并联导致所有东西都被短路
闭合开关后灯泡不亮电流表几乎无示数电压表所呈示数几乎为电源电压 灯泡断路故电压表串联到了电路中或电流表与电压表位置互换
闭合开关后无论怎样移动滑动变阻器的滑片灯泡亮度与两表示数均无改变 变阻器没有按照一上一下的方法来接
闭合开关后,无论怎样移动滑片灯泡都不亮 电路某一处断路或灯泡被导线或电流表短路
例1、下列对物理量的理解不恰当的是( )
A.对于定值电阻尽管有R,但是R并不与U成正比
B.对于同种物质尽管有ρ,但是ρ并不与m成正比
C.对于同一受力面尽管有p,但是p并不与F成正比
D.匀速运动的物体尽管有v,但是v并不与s成正比
例2、如图甲是非接触式红外线测温枪,它是通过接收人体辐射的红外线来显示被测人的体温。
(1)图乙是它的工作原理图,R是滑动变阻器,R0是热敏电阻,当人体温度升高时,电压表示数将变小。
①则其所用的热敏电阻阻值随温度变化的特点是图丙中的 曲线。
②为随着环境温度的升高,测量设备常会在无人通过时报警,为防止误报,应将滑动变阻器的滑片向 滑动。
(2)若上题中热敏电阻R0在检测到体温达到37.3℃的人体而报警时,其阻值为150Ω,报警电压为1.5V,电源电压恒定为5V,则此时滑动变阻器R接入电路的阻值为 。
例3、小金用如图甲所示的电路图,研究通过导体的电流与导体电阻的关系,电源电压为6V。改变电阻R的阻值,调节滑动变阻器滑片,保持R两端的电压不变,记下相应的4次实验的电流和电阻值,描绘在乙图中。
(1)实验开始时,小金根据甲电路图连接好电路,闭合开关,发现电压表有示数,电流表没有示数,则此次电路的故障可能是 ,小金排除故障后继续实验。
(2)实验过程中,移动滑动变阻器滑片时,眼睛应注视 ;
A.滑动变阻器B.电压表示数C.电流表示数
(3)根据图乙中所描的点可知,该实验中所选用的滑动变阻器的阻值至少为 欧;
(4)小金发现图像中每次描出的点与两坐标轴围成的面积(如图乙中阴影部分)总是相等,根据题意可知其原因是 。
例4、在“探究电流与电阻关系”的实验时,为了使实验操作简便,小敏用电阻箱来代替不同的定值电阻,电阻箱能提供的阻值是0~9999欧之间的任意整数值。现提供的器材有:电源(恒为6伏)、滑动变阻器(1安 50欧)、电压表(0~3伏)、电流表(0~0.6安)、电阻箱、开关和导线若干。
(1)请完成实物图甲的连接(要求滑片在最右端时滑动变阻器接入阻值最大)。
(2)实验中滑动变阻器的作用是 。
(3)实验开始时,调节电阻箱使接入阻值为5欧,闭合开关,再调节滑片使电压表示数达到设定值,电流表示数如图乙所示,则此时电压表示数为 2 伏。
(4)小敏多次改变电阻箱的接入阻值,测得相应电流,并得出了实验结论。根据所给量程和设定电压,电阻箱可调节的范围为 。
1.为了研究小灯泡电流与电压的关系,小明选择额定电压为2.5伏的小灯泡、电压为4伏的电源以及其它相关器材按图甲连接电路,进行实验。
(1)在实验过程中,小明将滑动变阻器的滑片从A端开始移动,直到灯泡正常发光,在此过程中测得小灯泡电流和电压的几组数据,并正确画出曲线a,如图乙所示。该实验中小明选择的滑动变阻器可能是 。
A、滑动变阻器R1(20欧,3安)
B、滑动变阻器R2(50欧,2安)
C、滑动变阻器R3(2000欧,0.25安)
(2)小明在图乙中还画出了本实验中滑动变阻器的电流随电压变化的曲线b,老师据图指出该曲线是错误的,其理由是 。
2.如图甲所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器R2的滑片P由a端移动到b端,测得电阻R1两端的电压与通过R1的电流的变化关系如图乙所示。则:
(1)变阻器R2的最大阻值为 。
(2)变阻器R2两端电压的变化范围为 。
3.用如图所示的电路图研究“电流与电阻的关系”。电流表量程为“0—0.6A”,电压表量程为“0—3V”,滑动变阻器的规格为“50Ω 1A”,电源电压3伏恒定不变。在AB间分别接入阻值不同的电阻R,移动滑动变阻器的滑片,读出电流表示数并记录。
(1)分析表中数据,可得出的实验结论是 ;
(2)为了使实验结论更可靠,应该 ,再多测几组数据,AB间允许接入电阻R的取值范围是 欧。
实验组次 1 2 3
电阻R/欧 5 10 20
电流I/安 0.4 0.2 0.1
4.随着科技的进步,智能设备逐步走入千家万户,某科研小组对自动储水装置进行研究。图甲的储水容器底有一个质量0.5千克、底面积100平方厘米的长方体浮桶,桶上端通过轻质弹簧与紧贴力敏电阻的轻质绝缘片A相连,距容器底0.4米处的侧壁有排水双控阀门。控制电路如图乙所示,其电源电压U为12伏,此时滑动变阻器接入电路的阻值为10欧,当电流表示数为0.6安,且桶底升至阀门所处高度时,阀门才感应排水。力敏电阻R与它所受压力F的对应关系如表所示(弹簧均在弹性限度内)。
压力F/牛 2 4 …… 12 15
电阻R/欧 110 70 …… 16 10
(1)未加水时,力敏电阻所受压力为2牛,电流表的示数是多少安?
(2)当双控阀门打开排水时,此时容器内水面距底部的距离为多少米?
(3)若要增加该装置的储水量,应如何调节控制电路中的滑动变阻器?并说明理由。
1.如图甲所示,电源电压恒为9伏,滑动变阻器的最大阻值为100欧,电流在0.1~0.4安之间时电子元件均能正常工作。若通过此电子元件的电流与其两端电压的关系如图乙所示,据此回答下列问题:
(1)电子元件处于正常工作状态时,通过电子元件的电流为I1,通过滑动变阻器的电流为I2,则I1 I2(填“>”“=”或“<”)。
(2)为使电子元件处于正常工作状态,滑动变阻器接入电路的最大阻值为 欧。
2.研究小组同学设计实验探究“电流与电阻的关系”。
【实验器材】
两节新干电池,滑动变阻器(10Ω,1A),电流表(0~0.6A、0~3A),电压表(0~3V、0~15V),定值电阻(2Ω、4Ω、6Ω、8Ω),开关,导线若干(所有器材均完好)。
【实验探究】
小组同学连接的电路如图甲所示,检查后发现有一根导线连接错误。
(1)图甲电路开关闭合后,电流表、电压表会出现的现象是 ;
(2)找出图甲中连接错误的导线并画“×”,再补充一根导线,使电路连接正确;
(3)正确连接电路,依次接入电阻进行实验,实验中出现如图乙所示情况,为了此次读数更精确,在不更换电路元件的前提下,需要做的调整是 ;
【问题讨论】
(4)为确保电路安全,并能使所有定值电阻接入电路都能完成实验,定值电阻两端电压最大不能超过 V。
3.小舟和小嘉两位同学分别探究“电流和电阻的关系”。小舟探究过程如下:
【实验步骤】
Ⅰ.根据设计的方案将阻值为5Ω的电阻接入电路,闭合开关,调节滑动变阻器的滑片,观察并记录相关数据;
Ⅱ.换用阻值为10Ω、20Ω的电阻,重复上述过程。
次数 电阻/Ω 电流/A
1 5 0.30
2 10 0.20
3 20 0.12
请你用笔画线代替导线,将电压表接入图甲电路中。
【得出结论】小舟对记录的数据进行处理,并绘制成图乙,据此得出的结论是 。
【交流反思】小嘉用和小舟同样的器材进行实验却无法得出正确结论,其记录的数据如表所示,请你帮他分析原因: 。
答案及解析
例1、解:
A、对于定值电阻尽管有R,但是R大小与导体的材料、长度、横截面积和温度有关,与U无关,故R并不与U成正比,故A正确;
B、物体的密度与物质的种类有关,种类和状态不变,密度不变,故B正确;
C、对于同一受力面,受力面积不变,根据p可知,p与F成正比,故C错误;
D、匀速运动的物体的速度不变,与路程无关,故D正确。
故选:C。
例2、解:由图乙可知,滑动变阻器R和热敏电阻R0串联接入电路,电压表测量热敏电阻R0两端的电压,
(1)①当人体温度升高时,电压表示数将减小,根据串联电路电压规律可知,滑动变阻器R两端的电压增大,根据欧姆定律可知,通过滑动变阻器的电流增大,即电路中的电流增大,根据欧姆定律可知,当电源电压一定时,电路中的总电阻减小,根据串联电路电阻规律可知,热敏电阻的阻值将减小,即人体温度升高时热敏电阻的阻值减小,故图丙中表示热敏电阻R0的阻值随温度变化的特点是A曲线;
②随着环境温度的升高,测量设备常会在无人通过时报警,由此①可知,温度升高,电压表示数减小,防止无人通过时报警,即要增大热敏电阻两端的电压,根据串联电路分压规律可知,滑动变阻器两端的电压减小,由此可知滑动变阻器接入电路的阻值减小,即滑动变阻器的滑片P向左移动;
(2)热敏电阻R0在检测到体温达到37.3℃的人体而报醫时,通过热敏电阻R0的电流I00.01A,通过滑动变阻器R的电流I滑=I0=0.01A,此时滑动变阻器R两端的电压U滑=U﹣U0=5V﹣1.5V=3.5V,滑动变阻器R接入电路的阻值R滑350Ω。
故答案为:(1)①A;②左;(3)350Ω。
例3、解:(1)实验开始时,小金根据甲电路图连接好电路,闭合开关,电流表没有示数,则电路可能断路,电压表有示数,则电压表与电源接通,则此次电路的故障可能是定值电阻断路;
(2)研究通过导体的电流与导体电阻的关系,应控制定值电阻两端的电压不变,实验过程中,移动滑动变阻器滑片时,眼睛应注视电压表示数,故选B;
(3)实验中应控制定值电阻两端的电压不变,根据欧姆定律可知定值电阻两端的电压UV=IR=0.1A×20Ω=2V,
根据串联电路的电压特点特点可知滑动变阻器两端的电压U滑=U﹣UV=6V﹣2V=4V,根据串联分压特点可知:,
该实验中所选用的滑动变阻器的阻值至少为R滑=2R=2×20Ω=40Ω;
(4)图像中每次描出的点与两坐标轴围成的面积,实验中应控制定值电阻两端的电压不变,结合UV=IR可知图像中每次描出的点与两坐标轴围成的面积(如图乙中阴影部分)总是相等,根据题意可知其原因是:定值电阻两端的电压不变。
故答案为:(1)定值电阻断路;(2)B;(3)40;(4)定值电阻两端的电压不变。
例4、解:(1)滑动变阻器串联在电路中,滑片在最右端时滑动变阻器接入阻值最大,故滑动变阻器左下接线柱连入电路中,如图所示:
;
(2)探究电流与电阻的关系,应保持电阻两端的电压不变,因此实验中滑动变阻器的作用控制定值电阻两端的电压不变,同时还有保护电路的作用;
(3)由图乙可知,电流表的量程为0~0.6A,分度值为0.02A,示数为0.4A,则电阻箱两端的电压为:UV=IR=0.4A×5Ω=2V,即电压表的示数为2V;
(4)由(3)可知,电阻箱两端的电压始终保持UV=2V,根据串联电路电压的规律,变阻器分得的电压:U滑=U﹣UV=6V﹣2V=4V,则电阻箱两端的电压为变阻器分得电压的0.5倍,根据分压原理,当变阻器连入电路中的电阻最大50Ω时,电阻箱接入电路的电阻为:R大=0.5×50Ω=25Ω;因为滑动变阻器允许通过的最大电流为1A,电流表的量程为0~0.6A,由串联电路的电流特点可知,电路中允许通过的最大为0.6A,由欧姆定律可知,此时电阻箱接入电路的最小电阻:R小3.3Ω,由电阻箱的特点可知,电阻箱接入电路的最小电阻为4Ω,因此电阻箱可调节的范围为4Ω~25Ω。
故答案为:(1)如图所示;(2)保护电路和控制定值电阻两端的电压不变;(3)2;(4)4Ω~25Ω。
1.解:(1)原电路中,灯与变阻器串联,为保护电路,闭合开关前,变阻器连入电路中的电阻应最大,此时电路中的电流最小,由图a可知,滑片在A时对应的电压U1=0.5V,电流I=0.1A,根据串联电路电压的规律,变阻器的电压:
U滑=U﹣U1=4V﹣0.5V=3.5V,由欧姆定律I,变阻器的最大电阻:
R滑35Ω>20Ω;因0.3A>0.25A(滑动变阻器R3允许通过的最大电流),故只能选用滑动变阻器R2(50欧,2安)B;
(2)图乙中还画出了本实验中滑动变阻器的电流随电压变化的曲线b,根据串联电路电压的规律:电路的总电压等于各部分电压之和,故变阻器与灯的电压之和为4V,而图中曲线b与a交点处,电压之和大于4V,故曲线b是错误的。
故答案为:(1)B;(2)小灯泡与滑动变阻器串联,两者电压之和为4V,而图中曲线b与a交点处,电压之和大于4V,故曲线b是错误的。
2.解:由电路图可知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,电流表测电路中的电流。
(1)当滑片位于a端时,电路为R1的简单电路,电压表V1的示数即为电源的电压,由图乙可知,电源的电压U=24V;
当滑片位于b端时,变阻器接入电路中的电阻最大,电路中的电流最小,
由图图可知,R1两端的电压U1=8V,通过的电流I1=1A,
因串联电路中总电压等于各分电压之和,
所以,R2两端的电压:
U2=U﹣U1=24V﹣8V=16V,
因串联电路中各处的电流相等,
所以,变阻器R2的最大阻值:R216Ω;
(2)当滑片位于a端时,电路为R1的简单电路,电压表V2的示数最小为0V,
当滑片位于b端时,变阻器接入电路中的电阻最大,电压表V2的示数最大,最大为16V,所以变阻器R2两端电压的变化范围为0V~16V。
故答案为:(1)16Ω;(2)0V~16V。
3.解:(1)根据表中数据知:电流与电阻的乘积都为5Ω×0.4A=10Ω×0.2A=20Ω×0.1A=2V,故可以得出:电压一定时,导体中的电流与导体的电阻成反比;
(2)为了使实验结论更可靠,控制AB间电压2伏不变;
因电流表的量程为0~0.6A,滑动变阻器允许通过的最大电流为1A,
所以,为了保证电路的安全,电路中的最大电流为0.6A,此时定值电阻和滑动变阻器接入电路中的电阻都最小,
根据欧姆定律可知,此时电路中的定值电阻最小为:
R小3.3Ω;
因为滑动变阻器的最大电阻为50Ω,当滑动变阻器的电阻最大时,定值电阻阻值也最大;
根据串联分压原理和欧姆定律可知,此时电流的电流为:
I′0.02A;
定值电阻的最大值为:
R大100Ω,
故AB间允许接入电阻R的取值范围是3.3~100Ω。
故答案为:(1)电压一定时,导体中的电流与导体的电阻成反比;(2)保持AB间电压2V不变;3.3~100。
4.解:(1)由表格数据知,力敏电阻所受压力为2N时,力敏电阻的阻值为110Ω,电路的总电阻:R总=R0+R=10Ω+110Ω=120Ω;
电流表的示数为:I0.1A;
(2)浮桶的重力:G=mg=0.5kg×10N/kg=5N;
当电流表示数为0.6A,且桶底升至阀门所处高度时,阀门才感应排水,
此时电路中的总电阻:R总′20Ω,
此时力敏电阻的阻值:R′=R总′﹣R0=20Ω﹣10Ω=10Ω,
由表格数据知,此时力敏电阻所受压力为15N,根据物体间力的作用是相互的,所以弹簧给浮桶向下的压力也是15N,
浮桶受到竖直向上的浮力、竖直向下的重力和压力,这三个力平衡,
则此时浮桶受到的浮力:F浮=G+F=5N+15N=20N,
浮桶排开水的体积:V排2.0×10﹣3m3=2000cm3,
则浮桶浸入水中的深度为:h120cm=0.20m,
当电流表示数为0.6A,且桶底升至阀门所处高度时,阀门才感应排水,
所以此时容器内水的深度:h=h1+h2=0.20m+0.4m=0.60m;
(3)水的压力越大时,压敏电阻的阻值越小,电路的总电阻越小,根据欧姆定律可知,电路中的电流越大;当电流表的示数最大时,该装置测量的压力最大,由电流表的量程一定可知,最大测量时的示数一定,由R可知,最大测量时电路的总电阻一定,要增加该装置的储水量,压敏电阻的阻值越小,则滑动变阻器的阻值越大,所以滑片应向下移动。
答:(1)未加水时,力敏电阻所受压力为2牛,电流表的示数是0.1A;
(2)当双控阀门打开排水时,此时容器内水面距底部的距离为0.60m;
(3)滑动变阻器的滑片向下移动;最大测量时电路的总电阻一定,要增加该装置的储水量,压敏电阻的阻值越小,则滑动变阻器的阻值越大。
1.解:(1)根据图甲可知,电子元件和变阻器串联,根据“串联电路各处电流都相等”的规律可知,电流I1=I2。
(3)根据乙图可知,通过电路的最小电流为0.1A,此时电子元件的电压为2V,
因串联电路两端电压等于各部分电压之和,所以滑动变阻器的电压:U滑=U总﹣U=9V﹣2V=7V;
由I可得,滑动变阻器接入的最大阻值:R滑70Ω。
故答案为:=;70。
2.解:(1)由于电压表的电阻很大,在电路中相当于开路,电路中的电流几乎为零,所以电流表几乎没有示数;电压表此时相当于测量电源电压,所以电压表示数接近3V;
(2)原电路中,电流表与电阻并联,电压表串联在电路中是错误的,电流表应与电阻串联,电压表与电阻并联,电流通过开关回到电源负极,如下图所示:
(3)由图乙指针的偏转情况可知,电流表所接的量程太大,所以要换用0~0.6A的小量程进行实验;
(4)根据题意可知,滑动变阻器允许通过的最大电流为1A,为确保电路安全,电路中的最大电流为I大=1A,
当使用2Ω的定值电阻进行实验时,根据欧姆定律可知,定值电阻两端的电压U大=I大R=1A×2Ω=2V;
当定值电阻两端的电压大于2V时,2Ω的定值就不能用来实验,所以定值电阻两端电压最大不能超过2V。
故答案为:(1)电流表几乎没有示数,电压表示数接近3V;(2)见解析;(3)电流表改接0~0.6A量程;(4)2。
3.解:(1)由图知电源电压为3V,所以电压表选择0~3V的量程与定值电阻并联,见下图:
(2)由图象可知,电流与电阻的乘积为:U=IR=0.4A×5Ω=﹣﹣﹣=0.1A×20Ω=﹣﹣﹣=2V,为一定值,故可得出结论:在电压一定时,导体中的电流与导体的电阻成反比;
(3)在探究电流与电阻的关系时需要控制电阻两端的电压不变,由表格数据知5Ω×0.30A≠10Ω×0.20A≠20Ω×0.12A,即电流与电阻的乘积不是定值,即没有保持电阻两端的电压不变,所以无法得出正确结论。
故答案为:(1)见解答图;(2)在电压一定时,导体中的电流与导体的电阻成反比;(3)没有保持电阻两端的电压不变。
2023浙教版科学中考第一轮复习--物理模块(十四)
欧姆定律与电路计算
1.探究电流与电压、电阻的关系
控制变量法设计对照实验:
①保持电阻不变,改变电压研究电流随电压的变化关系;
②保持电压不变,改变电阻研究电流随电阻的变化关系。
实验结论:
①在电阻一定的情况下,导体中的电流与加在导体两端的电压成正比;
②在电压一定的情况下,导体中的电流与导体的电阻成反比。
2.欧姆定律的内容:导体中的电流,跟这段导体两端的电压成正比,跟这段导体的电阻成反比。数学表达式:I=U/R
【注意】
1.欧姆定律适用于纯电阻电路。所谓纯电阻电路指用电器工作时,消耗的电能完全转化为内能的电路,含电动机的电路不能直接用欧姆定律计算。
2.I、U、R对应同一导体或同一段电路,不同时刻、不同导体或不同段电路三者不能混用。
3.同一导体(即R一定时),则I与U成正比;同一电源(即U一定时),则I与R成反比,不能说成是R与I成反比。
4.导体的电阻由导体本身的长度、横截面积、材料、温度等因素决定。电阻值可通过欧姆定律变形公式R=U/I计算,R与U和I的比值有关,但R与外加电压U和通过电流I等因素无关,即使电阻两端没有外加电压,内部没有电流通过,电阻依然存在。
二、伏安法测电阻
1.用电压表和电流表分别测出电路中某一导体两端的电压和通过的电流,就可以根据欧姆定律算出这个导体的电阻,这种用电压表和电流表测电阻的方法叫伏安法。
伏安法测电阻原理:I=U/R。电路图如下:
2.实验步骤
①连接实物电路。连接实物时先断开开关;滑动变阻器“一上一下”连接,并将其调到最大阻值处。连接电流表和电压表时注意“+”进“-”出及选择正确的量程。
②检查电路无误后,闭合开关S,三次改变滑动变阻器的阻值,分别读出电流表和电压表的示数,填入表格。
③算出三次Rx的值,求出平均值。
④整理器材。
三、串、并联电路的特点
串联电路 并联电路
电路
电流 I=I1=I2 I=I1+I2
电压 U=U1+U2 U=U1=U2
电阻 R=R1+R2 1/R=1/R1+1/R2或R=
分压或分流 = =
四、欧姆电路动态分析
串联电路中电压与电阻成正比,即=(分压原理),因此串联电路中,电阻越大电压就越大,当其中一个电阻增大时,它两端的电压也会变大,又因为电路总电压不变,所以其他用电器的电压就会变小。并联电路中,电流与电阻成反比,即=(分流原理),因此串联电路中,电阻越大电流就越小。
步 骤:(1)判断用电器的串并联方式(电路较复杂时,电压表=断路;电流表=短路);
(2)弄清电表的测量对象;
(3)认清滑动变阻器滑片的移动或开关开、闭对电路阻值的影响;
(4)利用欧姆定律及其变形公式,结合串联或并联电路的特点进行分析。
【总结】
常规分析方法:局部电阻变化→总电阻变化→总电流变化→局部电流、电压变化(先分析定值电阻的电流、电压的变化,再分析局部电阻变化的那部分电路的变化情况)
简便分析方法:“串反并同”或“大电阻大电压”即测量对象与变阻器串联时,变化与变阻器相同,反之相反。
五、欧姆定律故障分析
串联电路单故障判断方法
并联电路单故障判断方法
注 意:①在复杂电路故障判断时,先列出故障原因,再把电表变化现象列出,寻找合适选项。
②并联电路基本上不考短路故障,只会涉及电压表(测电源)与干路电流;因此重点需要放在串联电路故障分析上,增加总结环节。
总结:常见的电路故障及原因
故障 原因
闭合开关后,灯泡忽明忽暗,两表指针来回摆动 电路某处接触不良
闭合开关前灯泡发光,闭合开关后灯泡不亮了两表也无示数 开关与电源并联导致所有东西都被短路
闭合开关后灯泡不亮电流表几乎无示数电压表所呈示数几乎为电源电压 灯泡断路故电压表串联到了电路中或电流表与电压表位置互换
闭合开关后无论怎样移动滑动变阻器的滑片灯泡亮度与两表示数均无改变 变阻器没有按照一上一下的方法来接
闭合开关后,无论怎样移动滑片灯泡都不亮 电路某一处断路或灯泡被导线或电流表短路
例1、下列对物理量的理解不恰当的是( )
A.对于定值电阻尽管有R,但是R并不与U成正比
B.对于同种物质尽管有ρ,但是ρ并不与m成正比
C.对于同一受力面尽管有p,但是p并不与F成正比
D.匀速运动的物体尽管有v,但是v并不与s成正比
例2、如图甲是非接触式红外线测温枪,它是通过接收人体辐射的红外线来显示被测人的体温。
(1)图乙是它的工作原理图,R是滑动变阻器,R0是热敏电阻,当人体温度升高时,电压表示数将变小。
①则其所用的热敏电阻阻值随温度变化的特点是图丙中的 曲线。
②为随着环境温度的升高,测量设备常会在无人通过时报警,为防止误报,应将滑动变阻器的滑片向 滑动。
(2)若上题中热敏电阻R0在检测到体温达到37.3℃的人体而报警时,其阻值为150Ω,报警电压为1.5V,电源电压恒定为5V,则此时滑动变阻器R接入电路的阻值为 。
例3、小金用如图甲所示的电路图,研究通过导体的电流与导体电阻的关系,电源电压为6V。改变电阻R的阻值,调节滑动变阻器滑片,保持R两端的电压不变,记下相应的4次实验的电流和电阻值,描绘在乙图中。
(1)实验开始时,小金根据甲电路图连接好电路,闭合开关,发现电压表有示数,电流表没有示数,则此次电路的故障可能是 ,小金排除故障后继续实验。
(2)实验过程中,移动滑动变阻器滑片时,眼睛应注视 ;
A.滑动变阻器B.电压表示数C.电流表示数
(3)根据图乙中所描的点可知,该实验中所选用的滑动变阻器的阻值至少为 欧;
(4)小金发现图像中每次描出的点与两坐标轴围成的面积(如图乙中阴影部分)总是相等,根据题意可知其原因是 。
例4、在“探究电流与电阻关系”的实验时,为了使实验操作简便,小敏用电阻箱来代替不同的定值电阻,电阻箱能提供的阻值是0~9999欧之间的任意整数值。现提供的器材有:电源(恒为6伏)、滑动变阻器(1安 50欧)、电压表(0~3伏)、电流表(0~0.6安)、电阻箱、开关和导线若干。
(1)请完成实物图甲的连接(要求滑片在最右端时滑动变阻器接入阻值最大)。
(2)实验中滑动变阻器的作用是 。
(3)实验开始时,调节电阻箱使接入阻值为5欧,闭合开关,再调节滑片使电压表示数达到设定值,电流表示数如图乙所示,则此时电压表示数为 2 伏。
(4)小敏多次改变电阻箱的接入阻值,测得相应电流,并得出了实验结论。根据所给量程和设定电压,电阻箱可调节的范围为 。
1.为了研究小灯泡电流与电压的关系,小明选择额定电压为2.5伏的小灯泡、电压为4伏的电源以及其它相关器材按图甲连接电路,进行实验。
(1)在实验过程中,小明将滑动变阻器的滑片从A端开始移动,直到灯泡正常发光,在此过程中测得小灯泡电流和电压的几组数据,并正确画出曲线a,如图乙所示。该实验中小明选择的滑动变阻器可能是 。
A、滑动变阻器R1(20欧,3安)
B、滑动变阻器R2(50欧,2安)
C、滑动变阻器R3(2000欧,0.25安)
(2)小明在图乙中还画出了本实验中滑动变阻器的电流随电压变化的曲线b,老师据图指出该曲线是错误的,其理由是 。
2.如图甲所示的电路中,电源电压保持不变,闭合开关S后,滑动变阻器R2的滑片P由a端移动到b端,测得电阻R1两端的电压与通过R1的电流的变化关系如图乙所示。则:
(1)变阻器R2的最大阻值为 。
(2)变阻器R2两端电压的变化范围为 。
3.用如图所示的电路图研究“电流与电阻的关系”。电流表量程为“0—0.6A”,电压表量程为“0—3V”,滑动变阻器的规格为“50Ω 1A”,电源电压3伏恒定不变。在AB间分别接入阻值不同的电阻R,移动滑动变阻器的滑片,读出电流表示数并记录。
(1)分析表中数据,可得出的实验结论是 ;
(2)为了使实验结论更可靠,应该 ,再多测几组数据,AB间允许接入电阻R的取值范围是 欧。
实验组次 1 2 3
电阻R/欧 5 10 20
电流I/安 0.4 0.2 0.1
4.随着科技的进步,智能设备逐步走入千家万户,某科研小组对自动储水装置进行研究。图甲的储水容器底有一个质量0.5千克、底面积100平方厘米的长方体浮桶,桶上端通过轻质弹簧与紧贴力敏电阻的轻质绝缘片A相连,距容器底0.4米处的侧壁有排水双控阀门。控制电路如图乙所示,其电源电压U为12伏,此时滑动变阻器接入电路的阻值为10欧,当电流表示数为0.6安,且桶底升至阀门所处高度时,阀门才感应排水。力敏电阻R与它所受压力F的对应关系如表所示(弹簧均在弹性限度内)。
压力F/牛 2 4 …… 12 15
电阻R/欧 110 70 …… 16 10
(1)未加水时,力敏电阻所受压力为2牛,电流表的示数是多少安?
(2)当双控阀门打开排水时,此时容器内水面距底部的距离为多少米?
(3)若要增加该装置的储水量,应如何调节控制电路中的滑动变阻器?并说明理由。
1.如图甲所示,电源电压恒为9伏,滑动变阻器的最大阻值为100欧,电流在0.1~0.4安之间时电子元件均能正常工作。若通过此电子元件的电流与其两端电压的关系如图乙所示,据此回答下列问题:
(1)电子元件处于正常工作状态时,通过电子元件的电流为I1,通过滑动变阻器的电流为I2,则I1 I2(填“>”“=”或“<”)。
(2)为使电子元件处于正常工作状态,滑动变阻器接入电路的最大阻值为 欧。
2.研究小组同学设计实验探究“电流与电阻的关系”。
【实验器材】
两节新干电池,滑动变阻器(10Ω,1A),电流表(0~0.6A、0~3A),电压表(0~3V、0~15V),定值电阻(2Ω、4Ω、6Ω、8Ω),开关,导线若干(所有器材均完好)。
【实验探究】
小组同学连接的电路如图甲所示,检查后发现有一根导线连接错误。
(1)图甲电路开关闭合后,电流表、电压表会出现的现象是 ;
(2)找出图甲中连接错误的导线并画“×”,再补充一根导线,使电路连接正确;
(3)正确连接电路,依次接入电阻进行实验,实验中出现如图乙所示情况,为了此次读数更精确,在不更换电路元件的前提下,需要做的调整是 ;
【问题讨论】
(4)为确保电路安全,并能使所有定值电阻接入电路都能完成实验,定值电阻两端电压最大不能超过 V。
3.小舟和小嘉两位同学分别探究“电流和电阻的关系”。小舟探究过程如下:
【实验步骤】
Ⅰ.根据设计的方案将阻值为5Ω的电阻接入电路,闭合开关,调节滑动变阻器的滑片,观察并记录相关数据;
Ⅱ.换用阻值为10Ω、20Ω的电阻,重复上述过程。
次数 电阻/Ω 电流/A
1 5 0.30
2 10 0.20
3 20 0.12
请你用笔画线代替导线,将电压表接入图甲电路中。
【得出结论】小舟对记录的数据进行处理,并绘制成图乙,据此得出的结论是 。
【交流反思】小嘉用和小舟同样的器材进行实验却无法得出正确结论,其记录的数据如表所示,请你帮他分析原因: 。
答案及解析
例1、解:
A、对于定值电阻尽管有R,但是R大小与导体的材料、长度、横截面积和温度有关,与U无关,故R并不与U成正比,故A正确;
B、物体的密度与物质的种类有关,种类和状态不变,密度不变,故B正确;
C、对于同一受力面,受力面积不变,根据p可知,p与F成正比,故C错误;
D、匀速运动的物体的速度不变,与路程无关,故D正确。
故选:C。
例2、解:由图乙可知,滑动变阻器R和热敏电阻R0串联接入电路,电压表测量热敏电阻R0两端的电压,
(1)①当人体温度升高时,电压表示数将减小,根据串联电路电压规律可知,滑动变阻器R两端的电压增大,根据欧姆定律可知,通过滑动变阻器的电流增大,即电路中的电流增大,根据欧姆定律可知,当电源电压一定时,电路中的总电阻减小,根据串联电路电阻规律可知,热敏电阻的阻值将减小,即人体温度升高时热敏电阻的阻值减小,故图丙中表示热敏电阻R0的阻值随温度变化的特点是A曲线;
②随着环境温度的升高,测量设备常会在无人通过时报警,由此①可知,温度升高,电压表示数减小,防止无人通过时报警,即要增大热敏电阻两端的电压,根据串联电路分压规律可知,滑动变阻器两端的电压减小,由此可知滑动变阻器接入电路的阻值减小,即滑动变阻器的滑片P向左移动;
(2)热敏电阻R0在检测到体温达到37.3℃的人体而报醫时,通过热敏电阻R0的电流I00.01A,通过滑动变阻器R的电流I滑=I0=0.01A,此时滑动变阻器R两端的电压U滑=U﹣U0=5V﹣1.5V=3.5V,滑动变阻器R接入电路的阻值R滑350Ω。
故答案为:(1)①A;②左;(3)350Ω。
例3、解:(1)实验开始时,小金根据甲电路图连接好电路,闭合开关,电流表没有示数,则电路可能断路,电压表有示数,则电压表与电源接通,则此次电路的故障可能是定值电阻断路;
(2)研究通过导体的电流与导体电阻的关系,应控制定值电阻两端的电压不变,实验过程中,移动滑动变阻器滑片时,眼睛应注视电压表示数,故选B;
(3)实验中应控制定值电阻两端的电压不变,根据欧姆定律可知定值电阻两端的电压UV=IR=0.1A×20Ω=2V,
根据串联电路的电压特点特点可知滑动变阻器两端的电压U滑=U﹣UV=6V﹣2V=4V,根据串联分压特点可知:,
该实验中所选用的滑动变阻器的阻值至少为R滑=2R=2×20Ω=40Ω;
(4)图像中每次描出的点与两坐标轴围成的面积,实验中应控制定值电阻两端的电压不变,结合UV=IR可知图像中每次描出的点与两坐标轴围成的面积(如图乙中阴影部分)总是相等,根据题意可知其原因是:定值电阻两端的电压不变。
故答案为:(1)定值电阻断路;(2)B;(3)40;(4)定值电阻两端的电压不变。
例4、解:(1)滑动变阻器串联在电路中,滑片在最右端时滑动变阻器接入阻值最大,故滑动变阻器左下接线柱连入电路中,如图所示:
;
(2)探究电流与电阻的关系,应保持电阻两端的电压不变,因此实验中滑动变阻器的作用控制定值电阻两端的电压不变,同时还有保护电路的作用;
(3)由图乙可知,电流表的量程为0~0.6A,分度值为0.02A,示数为0.4A,则电阻箱两端的电压为:UV=IR=0.4A×5Ω=2V,即电压表的示数为2V;
(4)由(3)可知,电阻箱两端的电压始终保持UV=2V,根据串联电路电压的规律,变阻器分得的电压:U滑=U﹣UV=6V﹣2V=4V,则电阻箱两端的电压为变阻器分得电压的0.5倍,根据分压原理,当变阻器连入电路中的电阻最大50Ω时,电阻箱接入电路的电阻为:R大=0.5×50Ω=25Ω;因为滑动变阻器允许通过的最大电流为1A,电流表的量程为0~0.6A,由串联电路的电流特点可知,电路中允许通过的最大为0.6A,由欧姆定律可知,此时电阻箱接入电路的最小电阻:R小3.3Ω,由电阻箱的特点可知,电阻箱接入电路的最小电阻为4Ω,因此电阻箱可调节的范围为4Ω~25Ω。
故答案为:(1)如图所示;(2)保护电路和控制定值电阻两端的电压不变;(3)2;(4)4Ω~25Ω。
1.解:(1)原电路中,灯与变阻器串联,为保护电路,闭合开关前,变阻器连入电路中的电阻应最大,此时电路中的电流最小,由图a可知,滑片在A时对应的电压U1=0.5V,电流I=0.1A,根据串联电路电压的规律,变阻器的电压:
U滑=U﹣U1=4V﹣0.5V=3.5V,由欧姆定律I,变阻器的最大电阻:
R滑35Ω>20Ω;因0.3A>0.25A(滑动变阻器R3允许通过的最大电流),故只能选用滑动变阻器R2(50欧,2安)B;
(2)图乙中还画出了本实验中滑动变阻器的电流随电压变化的曲线b,根据串联电路电压的规律:电路的总电压等于各部分电压之和,故变阻器与灯的电压之和为4V,而图中曲线b与a交点处,电压之和大于4V,故曲线b是错误的。
故答案为:(1)B;(2)小灯泡与滑动变阻器串联,两者电压之和为4V,而图中曲线b与a交点处,电压之和大于4V,故曲线b是错误的。
2.解:由电路图可知,R1与R2串联,电压表V1测R1两端的电压,电压表V2测R2两端的电压,电流表测电路中的电流。
(1)当滑片位于a端时,电路为R1的简单电路,电压表V1的示数即为电源的电压,由图乙可知,电源的电压U=24V;
当滑片位于b端时,变阻器接入电路中的电阻最大,电路中的电流最小,
由图图可知,R1两端的电压U1=8V,通过的电流I1=1A,
因串联电路中总电压等于各分电压之和,
所以,R2两端的电压:
U2=U﹣U1=24V﹣8V=16V,
因串联电路中各处的电流相等,
所以,变阻器R2的最大阻值:R216Ω;
(2)当滑片位于a端时,电路为R1的简单电路,电压表V2的示数最小为0V,
当滑片位于b端时,变阻器接入电路中的电阻最大,电压表V2的示数最大,最大为16V,所以变阻器R2两端电压的变化范围为0V~16V。
故答案为:(1)16Ω;(2)0V~16V。
3.解:(1)根据表中数据知:电流与电阻的乘积都为5Ω×0.4A=10Ω×0.2A=20Ω×0.1A=2V,故可以得出:电压一定时,导体中的电流与导体的电阻成反比;
(2)为了使实验结论更可靠,控制AB间电压2伏不变;
因电流表的量程为0~0.6A,滑动变阻器允许通过的最大电流为1A,
所以,为了保证电路的安全,电路中的最大电流为0.6A,此时定值电阻和滑动变阻器接入电路中的电阻都最小,
根据欧姆定律可知,此时电路中的定值电阻最小为:
R小3.3Ω;
因为滑动变阻器的最大电阻为50Ω,当滑动变阻器的电阻最大时,定值电阻阻值也最大;
根据串联分压原理和欧姆定律可知,此时电流的电流为:
I′0.02A;
定值电阻的最大值为:
R大100Ω,
故AB间允许接入电阻R的取值范围是3.3~100Ω。
故答案为:(1)电压一定时,导体中的电流与导体的电阻成反比;(2)保持AB间电压2V不变;3.3~100。
4.解:(1)由表格数据知,力敏电阻所受压力为2N时,力敏电阻的阻值为110Ω,电路的总电阻:R总=R0+R=10Ω+110Ω=120Ω;
电流表的示数为:I0.1A;
(2)浮桶的重力:G=mg=0.5kg×10N/kg=5N;
当电流表示数为0.6A,且桶底升至阀门所处高度时,阀门才感应排水,
此时电路中的总电阻:R总′20Ω,
此时力敏电阻的阻值:R′=R总′﹣R0=20Ω﹣10Ω=10Ω,
由表格数据知,此时力敏电阻所受压力为15N,根据物体间力的作用是相互的,所以弹簧给浮桶向下的压力也是15N,
浮桶受到竖直向上的浮力、竖直向下的重力和压力,这三个力平衡,
则此时浮桶受到的浮力:F浮=G+F=5N+15N=20N,
浮桶排开水的体积:V排2.0×10﹣3m3=2000cm3,
则浮桶浸入水中的深度为:h120cm=0.20m,
当电流表示数为0.6A,且桶底升至阀门所处高度时,阀门才感应排水,
所以此时容器内水的深度:h=h1+h2=0.20m+0.4m=0.60m;
(3)水的压力越大时,压敏电阻的阻值越小,电路的总电阻越小,根据欧姆定律可知,电路中的电流越大;当电流表的示数最大时,该装置测量的压力最大,由电流表的量程一定可知,最大测量时的示数一定,由R可知,最大测量时电路的总电阻一定,要增加该装置的储水量,压敏电阻的阻值越小,则滑动变阻器的阻值越大,所以滑片应向下移动。
答:(1)未加水时,力敏电阻所受压力为2牛,电流表的示数是0.1A;
(2)当双控阀门打开排水时,此时容器内水面距底部的距离为0.60m;
(3)滑动变阻器的滑片向下移动;最大测量时电路的总电阻一定,要增加该装置的储水量,压敏电阻的阻值越小,则滑动变阻器的阻值越大。
1.解:(1)根据图甲可知,电子元件和变阻器串联,根据“串联电路各处电流都相等”的规律可知,电流I1=I2。
(3)根据乙图可知,通过电路的最小电流为0.1A,此时电子元件的电压为2V,
因串联电路两端电压等于各部分电压之和,所以滑动变阻器的电压:U滑=U总﹣U=9V﹣2V=7V;
由I可得,滑动变阻器接入的最大阻值:R滑70Ω。
故答案为:=;70。
2.解:(1)由于电压表的电阻很大,在电路中相当于开路,电路中的电流几乎为零,所以电流表几乎没有示数;电压表此时相当于测量电源电压,所以电压表示数接近3V;
(2)原电路中,电流表与电阻并联,电压表串联在电路中是错误的,电流表应与电阻串联,电压表与电阻并联,电流通过开关回到电源负极,如下图所示:
(3)由图乙指针的偏转情况可知,电流表所接的量程太大,所以要换用0~0.6A的小量程进行实验;
(4)根据题意可知,滑动变阻器允许通过的最大电流为1A,为确保电路安全,电路中的最大电流为I大=1A,
当使用2Ω的定值电阻进行实验时,根据欧姆定律可知,定值电阻两端的电压U大=I大R=1A×2Ω=2V;
当定值电阻两端的电压大于2V时,2Ω的定值就不能用来实验,所以定值电阻两端电压最大不能超过2V。
故答案为:(1)电流表几乎没有示数,电压表示数接近3V;(2)见解析;(3)电流表改接0~0.6A量程;(4)2。
3.解:(1)由图知电源电压为3V,所以电压表选择0~3V的量程与定值电阻并联,见下图:
(2)由图象可知,电流与电阻的乘积为:U=IR=0.4A×5Ω=﹣﹣﹣=0.1A×20Ω=﹣﹣﹣=2V,为一定值,故可得出结论:在电压一定时,导体中的电流与导体的电阻成反比;
(3)在探究电流与电阻的关系时需要控制电阻两端的电压不变,由表格数据知5Ω×0.30A≠10Ω×0.20A≠20Ω×0.12A,即电流与电阻的乘积不是定值,即没有保持电阻两端的电压不变,所以无法得出正确结论。
故答案为:(1)见解答图;(2)在电压一定时,导体中的电流与导体的电阻成反比;(3)没有保持电阻两端的电压不变。
2023浙教版科学中考第一轮复习--物理模块(十四)
欧姆定律与电路计算
同课章节目录
