苏教版(2019)高中数学必修第二册 12.3_复数的几何意义_教学设计
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 12.3_复数的几何意义_教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 801.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 19:21:50 | ||
图片预览


文档简介
第十二章 复数
12.3 复数的几何意义
本章共分三小节,第一小节讲复数的概念,首先简要地说明了人们在解实数系方程的过程中,产生了扩充实数集的需要,从而自然地引入虚数单位i, 在此基础上,给出了复数的有关概念和复数的代数形式然后,通过了复数与复平面的点的一一对应,给出了复数的儿何意义,第二小节讲复数的运算,分别给出了复数的代数形式的加法、减法运算法则和复数的代数形式的乘法、除法的运算法则。第三小节讲数系的扩充,介绍了数集从自然数集开始,扩充到复数的过程,并说明了数系的每一次扩充,都解决了某些运算不能进行的矛盾。最后,说明了复数集内负数可以开平方的问题。
课程目标 学科素养
1.了解可以用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系. 2.掌握实轴、虚轴、模等概念. 3.理解向量加法、减法的几何意义,能用几何意义解决一些简单问题. a数学抽象: 通过复数代数形式及几何意义的理解提升数学抽象素养. b数学运算: 通过复数模的学习及应用培养数学运算素养.
1.教学重点:掌握实轴、虚轴、模等概念.
2.教学难点:理解向量加法、减法的几何意义,能用几何意义解决一些简单问题.
多媒体调试、讲义分发。
19世纪末20世纪初,著名的德国数学家高斯在证明代数基本定理时,首次引进“复数”这个名词,他把复数与平面内的点一一对应起来,创立了复平面,依赖平面内的点或有向线段(向量)建立了复数的几何基础.
复数的几何意义,从形的角度表明了复数的“存在性”,为进一步研究复数奠定了基础.
知识点一 复平面
建立了直角坐标系来表示复数的平面叫作复平面,x轴叫作实轴,y轴叫作虚轴.实轴上的点都表示实数;除原点外,虚轴上的点都表示纯虚数.
知识点二 复数的几何意义
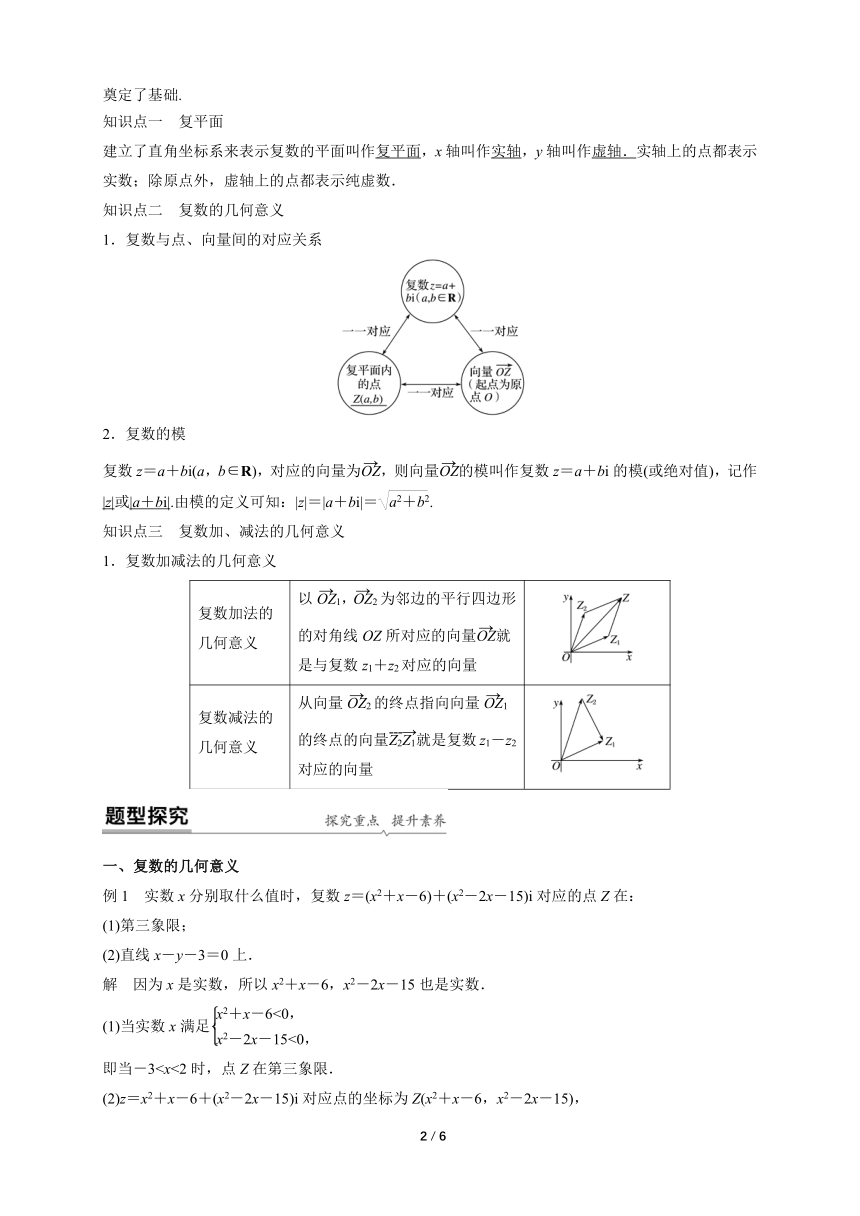
1.复数与点、向量间的对应关系
2.复数的模
复数z=a+bi(a,b∈R),对应的向量为,则向量的模叫作复数z=a+bi的模(或绝对值),记作|z|或|a+bi|.由模的定义可知:|z|=|a+bi|=.
知识点三 复数加、减法的几何意义
1.复数加减法的几何意义
复数加法的几何意义 以1,2为邻边的平行四边形的对角线OZ所对应的向量就是与复数z1+z2对应的向量
复数减法的几何意义 从向量2的终点指向向量1的终点的向量就是复数z1-z2对应的向量
一、复数的几何意义
例1 实数x分别取什么值时,复数z=(x2+x-6)+(x2-2x-15)i对应的点Z在:
(1)第三象限;
(2)直线x-y-3=0上.
解 因为x是实数,所以x2+x-6,x2-2x-15也是实数.
(1)当实数x满足
即当-3(2)z=x2+x-6+(x2-2x-15)i对应点的坐标为Z(x2+x-6,x2-2x-15),
当实数x满足(x2+x-6)-(x2-2x-15)-3=0,
即当x=-2时,点Z在直线x-y-3=0上.
延伸探究
若本例中的条件不变,其对应的点在:
(1)虚轴上;(2)第四象限.
解 (1)当实数x满足x2+x-6=0,
即当x=-3或2时,点Z在虚轴上.
(2)当实数x满足
即当2反思感悟 按照复数和复平面内所有点所构成的集合之间的一一对应关系,每一个复数都对应着一个有序实数对,只要在复平面内找出这个有序实数对所表示的点,就可根据点的位置判断复数实部、虚部的取值.
跟踪训练1 求当实数m为何值时,复数z=(m2-8m+15)+(m2+3m-28)i在复平面内的对应点分别满足下列条件:
(1)位于第四象限;
(2)位于x轴的负半轴上.
解 (1)由题意,知
解得
即-7故当-7(2)由题意,知
由②得m=-7或m=4.
因为m=-7不适合不等式①,m=4适合不等式①,
所以m=4.
故当m=4时,复数z的对应点位于x轴的负半轴上.
二、复数模及其几何意义的应用
例2 已知复数z1=-i及z2=-+i.
(1)求|z1|及|z2|的值;
(2)设z∈C,满足|z2|≤|z|≤|z1|的点Z的集合是什么图形?
解 (1)|z1|=|-i|==2,
|z2|== =1.
(2)由(1)知1≤|z|≤2,设z=x+yi(x,y∈R),
因为不等式|z|≥1的解集是圆x2+y2=1上和该圆外部所有点组成的集合,不等式|z|≤2的解集是圆x2+y2=4上和该圆内部所有点组成的集合,所以满足条件1≤|z|≤2的点Z的集合是以原点O为圆心,以1和2为半径的两圆所夹的圆环,并包括圆环的边界,如图所示.
反思感悟 (1)在计算复数的模时,应先找出复数的实部和虚部,然后再利用模的公式进行计算,两个虚数不能比较大小,但它们的模可以比较大小.
(2)复数的模表示该复数在复平面内对应的点到原点的距离.
跟踪训练2 设z为复数,且|z|=|z+1|=1,求|z-1|的值.
解 设z=a+bi(a,b∈R).
∵z+1=(a+1)+bi,且|z|=|z+1|=1,
∴∴即
即解得
∴|z-1|=|(a+bi)-1|=
==.
三、复数加、减法的几何意义
例3 如图所示,平行四边形OABC的顶点O,A,C分别对应的复数为0,3+2i,-2+4i.
求:(1)表示的复数;
(2)表示的复数;
(3)表示的复数.
解 因为A,C对应的复数分别为3+2i,-2+4i,
由复数的几何意义,知与表示的复数分别为3+2i,-2+4i.
(1)因为=-,所以表示的复数为-3-2i.
(2)因为=-,
所以表示的复数为(3+2i)-(-2+4i)=5-2i.
(3)因为=+,
所以表示的复数为(3+2i)+(-2+4i)=1+6i.
反思感悟 (1)常用技巧
①形转化为数:利用几何意义可以把几何图形的变换转化成复数运算去处理.
②数转化为形:对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
(2)常见结论:在复平面内,z1,z2对应的点分别为A,B,z1+z2对应的点为C,O为坐标原点,则
①四边形OACB为平行四边形.
②若|z1+z2|=|z1-z2|,则四边形OACB为矩形.
③若|z1|=|z2|,则四边形OACB为菱形.
④若|z1|=|z2|且|z1+z2|=|z1-z2|,则四边形OACB为正方形.
跟踪训练3 (1)已知复平面内的平面向量,表示的复数分别是-2+i,3+2i,则||=________.
答案
解析 ∵=+,
∴表示的复数为(-2+i)+(3+2i)=1+3i,
∴||==.
(2)若z1=2+i,z2=3+ai,复数z2-z1所对应的点在第四象限,则实数a的取值范围是______.
答案 (-∞,1)
解析 z2-z1=1+(a-1)i,
由题意知a-1<0,∴a<1.
1.若=(0,-3),则对应的复数为( )
A.0 B.-3 C.-3i D.3
答案 C
2.当A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案 D
解析 ∵∴复数z=(3m-2)+(m-1)i在复平面内对应的点位于第四象限.
3.若复数z=(m-2)+(m+1)i为纯虚数(i为虚数单位),其中m∈R,则|z|=________.
答案 3
解析 因为复数z=(m-2)+(m+1)i为纯虚数(i为虚数单位),
所以m-2=0且m+1≠0,解得m=2,所以z=3i,所以|z|=3.
4.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于第________象限.
答案 四
解析 ∵z1-z2=5-7i,∴z1-z2在复平面内对应的点为(5,-7),其位于第四象限.
5.设平行四边形ABCD在复平面内,A为原点,B,D两点对应的复数分别是3+2i和2-4i,则点C对应的复数是__________.
答案 5-2i
解析 方法一 由题意得,,表示的复数分别为3+2i,2-4i,
∵=+=3+2i+2-4i=5-2i,
∴点C对应的复数是5-2i.
方法二 设AC与BD的交点为E,则E点坐标为,设点C坐标为(x,y),则x=5,y=-2,故点C对应的复数为5-2i.
余弦定理与勾股定理的关系:余弦定理可以看作是勾股定理的推广,勾股定理可以看作是余弦定理的特例.
(1)如果一个三角形两边的平方和大于第三边的平方,那么第三边所对的角是锐角.
(2)如果一个三角形两边的平方和小于第三边的平方,那么第三边所对的角是钝角.
(3)如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角是直角.
2 / 6
12.3 复数的几何意义
本章共分三小节,第一小节讲复数的概念,首先简要地说明了人们在解实数系方程的过程中,产生了扩充实数集的需要,从而自然地引入虚数单位i, 在此基础上,给出了复数的有关概念和复数的代数形式然后,通过了复数与复平面的点的一一对应,给出了复数的儿何意义,第二小节讲复数的运算,分别给出了复数的代数形式的加法、减法运算法则和复数的代数形式的乘法、除法的运算法则。第三小节讲数系的扩充,介绍了数集从自然数集开始,扩充到复数的过程,并说明了数系的每一次扩充,都解决了某些运算不能进行的矛盾。最后,说明了复数集内负数可以开平方的问题。
课程目标 学科素养
1.了解可以用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系. 2.掌握实轴、虚轴、模等概念. 3.理解向量加法、减法的几何意义,能用几何意义解决一些简单问题. a数学抽象: 通过复数代数形式及几何意义的理解提升数学抽象素养. b数学运算: 通过复数模的学习及应用培养数学运算素养.
1.教学重点:掌握实轴、虚轴、模等概念.
2.教学难点:理解向量加法、减法的几何意义,能用几何意义解决一些简单问题.
多媒体调试、讲义分发。
19世纪末20世纪初,著名的德国数学家高斯在证明代数基本定理时,首次引进“复数”这个名词,他把复数与平面内的点一一对应起来,创立了复平面,依赖平面内的点或有向线段(向量)建立了复数的几何基础.
复数的几何意义,从形的角度表明了复数的“存在性”,为进一步研究复数奠定了基础.
知识点一 复平面
建立了直角坐标系来表示复数的平面叫作复平面,x轴叫作实轴,y轴叫作虚轴.实轴上的点都表示实数;除原点外,虚轴上的点都表示纯虚数.
知识点二 复数的几何意义
1.复数与点、向量间的对应关系
2.复数的模
复数z=a+bi(a,b∈R),对应的向量为,则向量的模叫作复数z=a+bi的模(或绝对值),记作|z|或|a+bi|.由模的定义可知:|z|=|a+bi|=.
知识点三 复数加、减法的几何意义
1.复数加减法的几何意义
复数加法的几何意义 以1,2为邻边的平行四边形的对角线OZ所对应的向量就是与复数z1+z2对应的向量
复数减法的几何意义 从向量2的终点指向向量1的终点的向量就是复数z1-z2对应的向量
一、复数的几何意义
例1 实数x分别取什么值时,复数z=(x2+x-6)+(x2-2x-15)i对应的点Z在:
(1)第三象限;
(2)直线x-y-3=0上.
解 因为x是实数,所以x2+x-6,x2-2x-15也是实数.
(1)当实数x满足
即当-3
当实数x满足(x2+x-6)-(x2-2x-15)-3=0,
即当x=-2时,点Z在直线x-y-3=0上.
延伸探究
若本例中的条件不变,其对应的点在:
(1)虚轴上;(2)第四象限.
解 (1)当实数x满足x2+x-6=0,
即当x=-3或2时,点Z在虚轴上.
(2)当实数x满足
即当2
跟踪训练1 求当实数m为何值时,复数z=(m2-8m+15)+(m2+3m-28)i在复平面内的对应点分别满足下列条件:
(1)位于第四象限;
(2)位于x轴的负半轴上.
解 (1)由题意,知
解得
即-7
由②得m=-7或m=4.
因为m=-7不适合不等式①,m=4适合不等式①,
所以m=4.
故当m=4时,复数z的对应点位于x轴的负半轴上.
二、复数模及其几何意义的应用
例2 已知复数z1=-i及z2=-+i.
(1)求|z1|及|z2|的值;
(2)设z∈C,满足|z2|≤|z|≤|z1|的点Z的集合是什么图形?
解 (1)|z1|=|-i|==2,
|z2|== =1.
(2)由(1)知1≤|z|≤2,设z=x+yi(x,y∈R),
因为不等式|z|≥1的解集是圆x2+y2=1上和该圆外部所有点组成的集合,不等式|z|≤2的解集是圆x2+y2=4上和该圆内部所有点组成的集合,所以满足条件1≤|z|≤2的点Z的集合是以原点O为圆心,以1和2为半径的两圆所夹的圆环,并包括圆环的边界,如图所示.
反思感悟 (1)在计算复数的模时,应先找出复数的实部和虚部,然后再利用模的公式进行计算,两个虚数不能比较大小,但它们的模可以比较大小.
(2)复数的模表示该复数在复平面内对应的点到原点的距离.
跟踪训练2 设z为复数,且|z|=|z+1|=1,求|z-1|的值.
解 设z=a+bi(a,b∈R).
∵z+1=(a+1)+bi,且|z|=|z+1|=1,
∴∴即
即解得
∴|z-1|=|(a+bi)-1|=
==.
三、复数加、减法的几何意义
例3 如图所示,平行四边形OABC的顶点O,A,C分别对应的复数为0,3+2i,-2+4i.
求:(1)表示的复数;
(2)表示的复数;
(3)表示的复数.
解 因为A,C对应的复数分别为3+2i,-2+4i,
由复数的几何意义,知与表示的复数分别为3+2i,-2+4i.
(1)因为=-,所以表示的复数为-3-2i.
(2)因为=-,
所以表示的复数为(3+2i)-(-2+4i)=5-2i.
(3)因为=+,
所以表示的复数为(3+2i)+(-2+4i)=1+6i.
反思感悟 (1)常用技巧
①形转化为数:利用几何意义可以把几何图形的变换转化成复数运算去处理.
②数转化为形:对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
(2)常见结论:在复平面内,z1,z2对应的点分别为A,B,z1+z2对应的点为C,O为坐标原点,则
①四边形OACB为平行四边形.
②若|z1+z2|=|z1-z2|,则四边形OACB为矩形.
③若|z1|=|z2|,则四边形OACB为菱形.
④若|z1|=|z2|且|z1+z2|=|z1-z2|,则四边形OACB为正方形.
跟踪训练3 (1)已知复平面内的平面向量,表示的复数分别是-2+i,3+2i,则||=________.
答案
解析 ∵=+,
∴表示的复数为(-2+i)+(3+2i)=1+3i,
∴||==.
(2)若z1=2+i,z2=3+ai,复数z2-z1所对应的点在第四象限,则实数a的取值范围是______.
答案 (-∞,1)
解析 z2-z1=1+(a-1)i,
由题意知a-1<0,∴a<1.
1.若=(0,-3),则对应的复数为( )
A.0 B.-3 C.-3i D.3
答案 C
2.当
C.第三象限 D.第四象限
答案 D
解析 ∵
3.若复数z=(m-2)+(m+1)i为纯虚数(i为虚数单位),其中m∈R,则|z|=________.
答案 3
解析 因为复数z=(m-2)+(m+1)i为纯虚数(i为虚数单位),
所以m-2=0且m+1≠0,解得m=2,所以z=3i,所以|z|=3.
4.设z1=3-4i,z2=-2+3i,则z1-z2在复平面内对应的点位于第________象限.
答案 四
解析 ∵z1-z2=5-7i,∴z1-z2在复平面内对应的点为(5,-7),其位于第四象限.
5.设平行四边形ABCD在复平面内,A为原点,B,D两点对应的复数分别是3+2i和2-4i,则点C对应的复数是__________.
答案 5-2i
解析 方法一 由题意得,,表示的复数分别为3+2i,2-4i,
∵=+=3+2i+2-4i=5-2i,
∴点C对应的复数是5-2i.
方法二 设AC与BD的交点为E,则E点坐标为,设点C坐标为(x,y),则x=5,y=-2,故点C对应的复数为5-2i.
余弦定理与勾股定理的关系:余弦定理可以看作是勾股定理的推广,勾股定理可以看作是余弦定理的特例.
(1)如果一个三角形两边的平方和大于第三边的平方,那么第三边所对的角是锐角.
(2)如果一个三角形两边的平方和小于第三边的平方,那么第三边所对的角是钝角.
(3)如果一个三角形两边的平方和等于第三边的平方,那么第三边所对的角是直角.
2 / 6
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
