苏教版(2019)高中数学必修第一册 《函数的奇偶性》精品课件(共13张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《函数的奇偶性》精品课件(共13张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 19:26:00 | ||
图片预览




文档简介
(共13张PPT)
苏教版同步教材精品课件
5.4函数的奇偶性
情境引入
在日常生活中,我们经常会接触到一些外形十分对称的物体,如飞翔的小鸟,美丽的蝴蝶,巴黎的埃菲尔铁塔,风车等.
这些对称的物体常常给我们一种美的感受,其实,这种美在我们数学里面也有大量的体现,这节课我们就来感受一下数学的对称美.
设计意图:通过实际生活中的例子,让学生对对称有一个初步的感性认识,为下一步对概念的理性认识做好铺垫.让学生感受到函数的奇偶性和我们的生活密切相关,进而激发学生的学习兴趣.
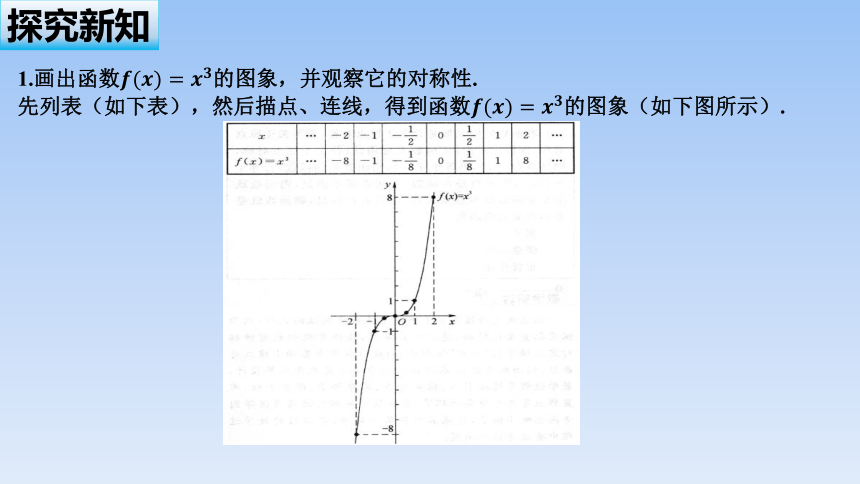
1.画出函数的图象,并观察它的对称性.
先列表(如下表),然后描点、连线,得到函数的图象(如下图所示).
探究新知
观察图象,发现函数的图象关于原点对称,并且当自变量取一对相反数时,它们的函数值也互为相反数,例如,事实上,对于函数的定义域内的任意一个x,都有,这时我们称函数为奇函数.
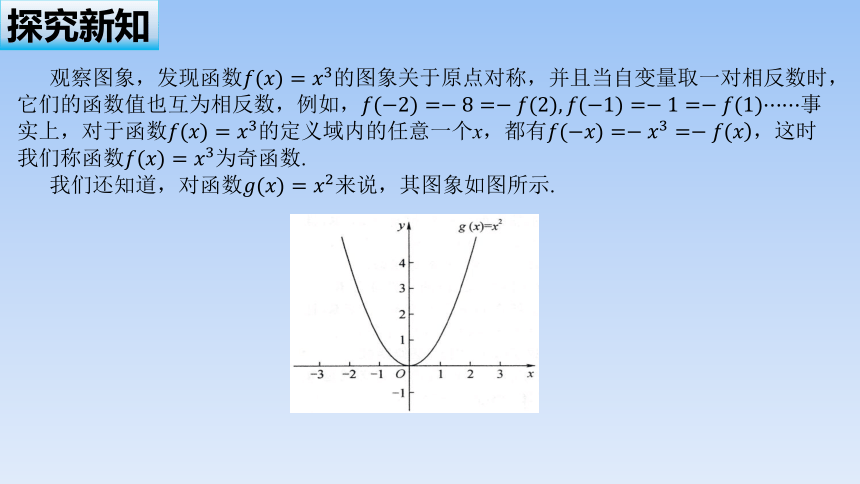
我们还知道,对函数来说,其图象如图所示.
探究新知
观察图象,发现函数的图象关于y轴对称,并且当自变量取一对相反数时,它们的函数值相等,例如,事实上,对于函数的定义域内的任意一个x,都有,这时我们称函数为偶函数.
探究新知
2.奇函数、偶函数的定义.
偶函数:一般地,设函数的定义域是A.如果对于任意的,都有,并且,那么称函数偶函数.
奇函数:一般地,设函数的定义域是A.如果对于任意的,都有,并且 ,那么称函数是奇函数.
如果函数是奇函数或偶函数,那么我们称函数具有奇偶性.
偶函数的图象关于y轴对称,奇函数的图象关于原点对称.
设计意图:理解函数奇偶性概念的形成过程,从中培养学生的观察、归纳能力,同时渗透数形结合和从特殊到般的数学思想方法,从知识体系的高度加深理解函数的奇偶性.
探究新知
重点强调:
(1)当函数是奇函数或偶函数时,称函数具有奇偶性.奇函数和偶函数的定义域均关于原点对称,如或.
(2)在研究一个函数时,如果知道它是奇函数或偶函数,就可以先研究它在非负区间上的性质,再利用对称性可知它在非正区间上的性质,从而减少工作量.
(3)具有奇偶性的函数的图象的特征:偶函数的图象关于y轴对称,奇函数的图象关于原点对称.
探究新知
典例剖析
例1、判定下列函数是否为偶函数或奇函数:
(1);(2);
(3);(4).
解析
(1)函数的定义域是R.
因为对于任意的,都有,且,
所以函数偶函数.
(2)函数的定义域是R.
因为对于任意的,都有,且,
所以函数是奇函数.
(3)函数的定义域是R.
因为对于任意的,都有,且,
所以函数是偶函数.
典例剖析
例1、判定下列函数是否为偶函数或奇函数:
(1);(2);
(3);(4).
解析
(4)函数的定义域是R.
因为,
所以.
因此,根据函数奇偶性定义可以知道,函数
既不是奇函数,也不是偶函数.
思考:判断函数奇偶性的方法是什么?
提示:看函数的定义域是否关于原点对称,若不关于原点对称,则得出结论:该函数无奇偶性;若关于原点对称,则计算,若等于,则函数是偶函数,若等于,则函数是奇函数,若两者都不满足,则函数既不是奇函数也不是偶函数,若两者都满足,则函数既是奇函数又是偶函数.
设计意图:理解并掌握判断函数奇偶性的方法,并明确根据奇偶性可将函数分为四类:奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数.
典例剖析
典例剖析
例2、判断函数是否具有奇偶性.
解析
函数的定义域为R.
因为对于任意的,都有,且
,
所以函数为奇函数.
设计意图:巩固函数奇偶性的判断方法.
课堂小结
通过这节课的学习,学生要能理清楚以下几个问题:
(1)单调性描述的是函数的变化规律,奇偶性描述的是函数的什么规律?
(2)偶函数和奇函数的定义分别是什么?
(3)判断函数的奇偶性的方法是什么?
作 业
教材第119页练习第5,6,7题.
苏教版同步教材精品课件
5.4函数的奇偶性
情境引入
在日常生活中,我们经常会接触到一些外形十分对称的物体,如飞翔的小鸟,美丽的蝴蝶,巴黎的埃菲尔铁塔,风车等.
这些对称的物体常常给我们一种美的感受,其实,这种美在我们数学里面也有大量的体现,这节课我们就来感受一下数学的对称美.
设计意图:通过实际生活中的例子,让学生对对称有一个初步的感性认识,为下一步对概念的理性认识做好铺垫.让学生感受到函数的奇偶性和我们的生活密切相关,进而激发学生的学习兴趣.
1.画出函数的图象,并观察它的对称性.
先列表(如下表),然后描点、连线,得到函数的图象(如下图所示).
探究新知
观察图象,发现函数的图象关于原点对称,并且当自变量取一对相反数时,它们的函数值也互为相反数,例如,事实上,对于函数的定义域内的任意一个x,都有,这时我们称函数为奇函数.
我们还知道,对函数来说,其图象如图所示.
探究新知
观察图象,发现函数的图象关于y轴对称,并且当自变量取一对相反数时,它们的函数值相等,例如,事实上,对于函数的定义域内的任意一个x,都有,这时我们称函数为偶函数.
探究新知
2.奇函数、偶函数的定义.
偶函数:一般地,设函数的定义域是A.如果对于任意的,都有,并且,那么称函数偶函数.
奇函数:一般地,设函数的定义域是A.如果对于任意的,都有,并且 ,那么称函数是奇函数.
如果函数是奇函数或偶函数,那么我们称函数具有奇偶性.
偶函数的图象关于y轴对称,奇函数的图象关于原点对称.
设计意图:理解函数奇偶性概念的形成过程,从中培养学生的观察、归纳能力,同时渗透数形结合和从特殊到般的数学思想方法,从知识体系的高度加深理解函数的奇偶性.
探究新知
重点强调:
(1)当函数是奇函数或偶函数时,称函数具有奇偶性.奇函数和偶函数的定义域均关于原点对称,如或.
(2)在研究一个函数时,如果知道它是奇函数或偶函数,就可以先研究它在非负区间上的性质,再利用对称性可知它在非正区间上的性质,从而减少工作量.
(3)具有奇偶性的函数的图象的特征:偶函数的图象关于y轴对称,奇函数的图象关于原点对称.
探究新知
典例剖析
例1、判定下列函数是否为偶函数或奇函数:
(1);(2);
(3);(4).
解析
(1)函数的定义域是R.
因为对于任意的,都有,且,
所以函数偶函数.
(2)函数的定义域是R.
因为对于任意的,都有,且,
所以函数是奇函数.
(3)函数的定义域是R.
因为对于任意的,都有,且,
所以函数是偶函数.
典例剖析
例1、判定下列函数是否为偶函数或奇函数:
(1);(2);
(3);(4).
解析
(4)函数的定义域是R.
因为,
所以.
因此,根据函数奇偶性定义可以知道,函数
既不是奇函数,也不是偶函数.
思考:判断函数奇偶性的方法是什么?
提示:看函数的定义域是否关于原点对称,若不关于原点对称,则得出结论:该函数无奇偶性;若关于原点对称,则计算,若等于,则函数是偶函数,若等于,则函数是奇函数,若两者都不满足,则函数既不是奇函数也不是偶函数,若两者都满足,则函数既是奇函数又是偶函数.
设计意图:理解并掌握判断函数奇偶性的方法,并明确根据奇偶性可将函数分为四类:奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数.
典例剖析
典例剖析
例2、判断函数是否具有奇偶性.
解析
函数的定义域为R.
因为对于任意的,都有,且
,
所以函数为奇函数.
设计意图:巩固函数奇偶性的判断方法.
课堂小结
通过这节课的学习,学生要能理清楚以下几个问题:
(1)单调性描述的是函数的变化规律,奇偶性描述的是函数的什么规律?
(2)偶函数和奇函数的定义分别是什么?
(3)判断函数的奇偶性的方法是什么?
作 业
教材第119页练习第5,6,7题.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
