山东省泰安高新区第一中学2013-2014学年青岛版九年级上期末模拟试题及答案
文档属性
| 名称 | 山东省泰安高新区第一中学2013-2014学年青岛版九年级上期末模拟试题及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 135.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-08 14:06:28 | ||
图片预览



文档简介
2013-2014学年上学期期末模拟测试
九年级数学试题
一.选择题(共15小题,每小题4分,共计60分)
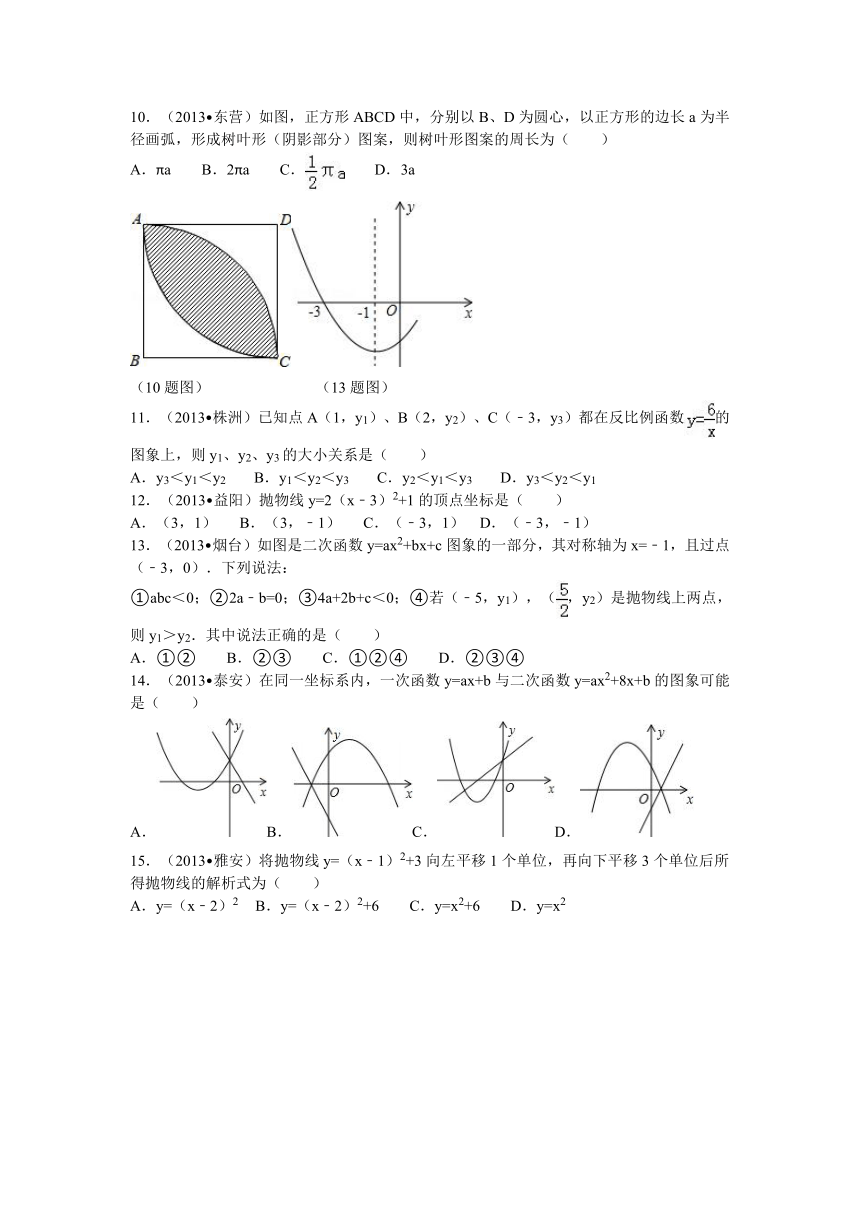
1.(2013 齐齐哈尔)下列数字中既是轴对称图形又是中心对称图形的有几个( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(2013 海南)如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD
(2题图) (4题图) (7题图) (8题图)
3.(2013 宜宾)矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
4.(2013 泰安)在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
5.(2013 威海)已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是( )
A.m≥﹣ B.m≥0 C.m≥1 D.m≥2
6.(2012 临沂)用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
7.(2013 兰州)如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )
A.3cm B.4cm C.5cm D.6cm
8.(2012 枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
A. B. C. D.
9.(2012 潍坊)已知两圆半径r1、r2分别是方程x2﹣7x+10=0的两根,两圆的圆心距为7,则两圆的位置关系是( )
A.相交 B.内切 C.外切 D.外离
10.(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
(10题图) (13题图)
11.(2013 株洲)已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数的图象上,则y1、y2、y3的大小关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y1
12.(2013 益阳)抛物线y=2(x﹣3)2+1的顶点坐标是( )
A.(3,1) B.(3,﹣1) C.(﹣3,1) D.(﹣3,﹣1)
13.(2013 烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:
①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A.①② B.②③ C.①②④ D.②③④
14.(2013 泰安)在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
A.B.C.D.
15.(2013 雅安)将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
A.y=(x﹣2)2 B.y=(x﹣2)2+6 C.y=x2+6 D.y=x2
答题栏
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共5小题,每小题3分,共计15分)
16.(2012 佳木斯)如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,请添加一个条件 _________ ,使四边形AECF是平行四边形(只填一个即可).
(16题图) (17题图) (18题图) (19题图)
17.(2013 盘锦)如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为 _________ .
18.(2013 聊城)如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 _________ .
19.(2013 天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为 _________ (度).
20.(2007 十堰)已知Rt△ABC的两直角边的长分别为6cm和8cm,则它的外接圆的半径与内切圆半径的比为 _________ .
三.解答题(共5小题)
21.(本大题8分)(2013 铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
22.(本大题8分)(2013 贵阳)2010年底某市汽车拥有量为100万辆,而截止到2012年底,该市的汽车拥有量已达到144万辆.
(1)求2010年底至2012年底该市汽车拥有量的年平均增长率;
(2)该市交通部门为控制汽车拥有量的增长速度,要求到2013年底全市汽车拥有量不超过155.52万辆,预计2013年报废的汽车数量是2012年底汽车拥有量的10%,求2012年底至2013年底该市汽车拥有量的年增长率要控制在什么范围才能达到要求.
23.(本大题8分)(2013 西宁)如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上,CE⊥AD于点E.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为8,CE=2,求CD的长.
24.(本大题9分)(2013 茂名)如图,反比例函数的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
25.(本大题12分)(2013 营口)如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2013-2014学年上学期期末模拟测试
九年级数学试题
参考答案与试题解析
一.选择题(每小题4分,共15小题,60分)
1.B. 2.D 3.B4.C 5.B 6.D7.C 8.B 9.C10.A11.D12.A13.C14.C 15.D
二.填空题(共5小题,每小题3分,共计15分)
16. AF=CE 17. 2 .18. 3 .19. 55 .20. 5:2 .
三.解答题(共5小题)
21. 解答: (1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
22. 解答: 解:(1)设2010年底至2012年底该市汽车拥有量的年平均增长率是x,
根据题意,100(1+x)2=144
1+x=±1.2
∴x1=0.2=20% x2=﹣2.2(不合题意,舍去)
答:2010年底至2012年底该市汽车拥有量的年平均增长率是20%.
(2)设2012年底到2013年底该市汽车拥有量的年平均增长率为y,
根据题意得:144(1+y)﹣144×10%≤155.52
解得:y≤0.18
答:2012年底至2013年底该市汽车拥有量的年增长率要控制在不超过18%能达到要求.
23. 解答: (1)证明:连接OA,∵BC为⊙O的直径,∴∠BAC=90°,∴∠B+∠ACB=90°,
∵OA=OC,∴∠OAC=∠OCA,
∵∠CAD=∠B,∴∠CAD+∠OAC=90°,即∠OAD=90°,∴OA⊥AD,∵点A在圆上,∴AD是⊙O的切线;
(2)解:∵CE⊥AD,∴∠CED=∠OAD=90°,∴CE∥OA,∴△CED∽△OAD,∴,CE=2,
设CD=x,则OD=x+8,即,解得x=,经检验x=是原分式方程的解,所以CD=.
24.解答: 解:(1)将A(m,3),B(﹣3,n)分别代入反比例解析式得:3=,n=,
解得:m=2,n=﹣2,∴A(2,3),B(﹣3,﹣2),
将A与B代入一次函数解析式得:,解得:,则一次函数解析式为y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴由函数图象得:反比例函数值大于一次函数值的自变量x的取值范围为x<﹣3或0<x<2.
25. 解答: 解:(1)设抛物线的解析式为y=ax2+bx+c
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.
把点A(1,0)、点B(﹣3,0)代入,得解得a=﹣1,b=﹣2
∴抛物线的解析式为y=﹣x2﹣2x+3.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4
∴顶点D的坐标为(﹣1,4);
(2)△BCD是直角三角形.
理由如下:解法一:过点D分别作x轴、y轴的垂线,垂足分别为E、F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
∴CD2=DF2+CF2=2
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=DE2+BE2=20
∴BC2+CD2=BD2
∴△BCD为直角三角形.
解法二:过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3
∴OB=OC∴∠OCB=45°
∵在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1
∴DF=CF
∴∠DCF=45°
∴∠BCD=180°﹣∠DCF﹣∠OCB=90°
∴△BCD为直角三角形.
(3)①△BCD的三边,==,又=,故当P是原点O时,△ACP∽△DBC;
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3﹣a,=,即=,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3﹣b,则=,即=,解得:b=﹣,故P是(0,﹣)时,则△ACP∽△CBD一定成立;
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1﹣d,当AC与CD是对应边时,=,即=,解得:d=1﹣3,此时,两个三角形不相似;
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1﹣e,当AC与DC是对应边时,=,即=,解得:e=﹣9,符合条件.
总之,符合条件的点P的坐标为:.
九年级数学试题
一.选择题(共15小题,每小题4分,共计60分)
1.(2013 齐齐哈尔)下列数字中既是轴对称图形又是中心对称图形的有几个( )
A. 1个 B. 2个 C. 3个 D. 4个
2.(2013 海南)如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO B.CD=AB C.∠BAD=∠BCD D.AC=BD
(2题图) (4题图) (7题图) (8题图)
3.(2013 宜宾)矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B. 对角线相等
C.对角线互相平分 D. 两组对角分别相等
4.(2013 泰安)在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
5.(2013 威海)已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是( )
A.m≥﹣ B.m≥0 C.m≥1 D.m≥2
6.(2012 临沂)用配方法解一元二次方程x2﹣4x=5时,此方程可变形为( )
A.(x+2)2=1 B.(x﹣2)2=1 C.(x+2)2=9 D.(x﹣2)2=9
7.(2013 兰州)如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )
A.3cm B.4cm C.5cm D.6cm
8.(2012 枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
A. B. C. D.
9.(2012 潍坊)已知两圆半径r1、r2分别是方程x2﹣7x+10=0的两根,两圆的圆心距为7,则两圆的位置关系是( )
A.相交 B.内切 C.外切 D.外离
10.(2013 东营)如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa B.2πa C. D.3a
(10题图) (13题图)
11.(2013 株洲)已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数的图象上,则y1、y2、y3的大小关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y1
12.(2013 益阳)抛物线y=2(x﹣3)2+1的顶点坐标是( )
A.(3,1) B.(3,﹣1) C.(﹣3,1) D.(﹣3,﹣1)
13.(2013 烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:
①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A.①② B.②③ C.①②④ D.②③④
14.(2013 泰安)在同一坐标系内,一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是( )
A.B.C.D.
15.(2013 雅安)将抛物线y=(x﹣1)2+3向左平移1个单位,再向下平移3个单位后所得抛物线的解析式为( )
A.y=(x﹣2)2 B.y=(x﹣2)2+6 C.y=x2+6 D.y=x2
答题栏
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案
二.填空题(共5小题,每小题3分,共计15分)
16.(2012 佳木斯)如图,在平行四边形ABCD中,点E、F分别在边BC、AD上,请添加一个条件 _________ ,使四边形AECF是平行四边形(只填一个即可).
(16题图) (17题图) (18题图) (19题图)
17.(2013 盘锦)如图,等腰梯形ABCD,AD∥BC,BD平分∠ABC,∠A=120°.若梯形的周长为10,则AD的长为 _________ .
18.(2013 聊城)如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 _________ .
19.(2013 天津)如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为 _________ (度).
20.(2007 十堰)已知Rt△ABC的两直角边的长分别为6cm和8cm,则它的外接圆的半径与内切圆半径的比为 _________ .
三.解答题(共5小题)
21.(本大题8分)(2013 铁岭)如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
22.(本大题8分)(2013 贵阳)2010年底某市汽车拥有量为100万辆,而截止到2012年底,该市的汽车拥有量已达到144万辆.
(1)求2010年底至2012年底该市汽车拥有量的年平均增长率;
(2)该市交通部门为控制汽车拥有量的增长速度,要求到2013年底全市汽车拥有量不超过155.52万辆,预计2013年报废的汽车数量是2012年底汽车拥有量的10%,求2012年底至2013年底该市汽车拥有量的年增长率要控制在什么范围才能达到要求.
23.(本大题8分)(2013 西宁)如图,⊙O是△ABC的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上,CE⊥AD于点E.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为8,CE=2,求CD的长.
24.(本大题9分)(2013 茂名)如图,反比例函数的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
25.(本大题12分)(2013 营口)如图,抛物线与x轴交于A(1,0)、B(﹣3,0)两点,与y轴交于点C(0,3),设抛物线的顶点为D.
(1)求该抛物线的解析式与顶点D的坐标.
(2)试判断△BCD的形状,并说明理由.
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
2013-2014学年上学期期末模拟测试
九年级数学试题
参考答案与试题解析
一.选择题(每小题4分,共15小题,60分)
1.B. 2.D 3.B4.C 5.B 6.D7.C 8.B 9.C10.A11.D12.A13.C14.C 15.D
二.填空题(共5小题,每小题3分,共计15分)
16. AF=CE 17. 2 .18. 3 .19. 55 .20. 5:2 .
三.解答题(共5小题)
21. 解答: (1)证明:∵点O为AB的中点,连接DO并延长到点E,使OE=OD,
∴四边形AEBD是平行四边形,
∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,∴∠ADB=90°,∴平行四边形AEBD是矩形;
(2)当∠BAC=90°时,理由:∵∠BAC=90°,AB=AC,AD是△ABC的角平分线,
∴AD=BD=CD,
∵由(1)得四边形AEBD是矩形,∴矩形AEBD是正方形.
22. 解答: 解:(1)设2010年底至2012年底该市汽车拥有量的年平均增长率是x,
根据题意,100(1+x)2=144
1+x=±1.2
∴x1=0.2=20% x2=﹣2.2(不合题意,舍去)
答:2010年底至2012年底该市汽车拥有量的年平均增长率是20%.
(2)设2012年底到2013年底该市汽车拥有量的年平均增长率为y,
根据题意得:144(1+y)﹣144×10%≤155.52
解得:y≤0.18
答:2012年底至2013年底该市汽车拥有量的年增长率要控制在不超过18%能达到要求.
23. 解答: (1)证明:连接OA,∵BC为⊙O的直径,∴∠BAC=90°,∴∠B+∠ACB=90°,
∵OA=OC,∴∠OAC=∠OCA,
∵∠CAD=∠B,∴∠CAD+∠OAC=90°,即∠OAD=90°,∴OA⊥AD,∵点A在圆上,∴AD是⊙O的切线;
(2)解:∵CE⊥AD,∴∠CED=∠OAD=90°,∴CE∥OA,∴△CED∽△OAD,∴,CE=2,
设CD=x,则OD=x+8,即,解得x=,经检验x=是原分式方程的解,所以CD=.
24.解答: 解:(1)将A(m,3),B(﹣3,n)分别代入反比例解析式得:3=,n=,
解得:m=2,n=﹣2,∴A(2,3),B(﹣3,﹣2),
将A与B代入一次函数解析式得:,解得:,则一次函数解析式为y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴由函数图象得:反比例函数值大于一次函数值的自变量x的取值范围为x<﹣3或0<x<2.
25. 解答: 解:(1)设抛物线的解析式为y=ax2+bx+c
由抛物线与y轴交于点C(0,3),可知c=3.即抛物线的解析式为y=ax2+bx+3.
把点A(1,0)、点B(﹣3,0)代入,得解得a=﹣1,b=﹣2
∴抛物线的解析式为y=﹣x2﹣2x+3.
∵y=﹣x2﹣2x+3=﹣(x+1)2+4
∴顶点D的坐标为(﹣1,4);
(2)△BCD是直角三角形.
理由如下:解法一:过点D分别作x轴、y轴的垂线,垂足分别为E、F.
∵在Rt△BOC中,OB=3,OC=3,
∴BC2=OB2+OC2=18
在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1,
∴CD2=DF2+CF2=2
在Rt△BDE中,DE=4,BE=OB﹣OE=3﹣1=2,
∴BD2=DE2+BE2=20
∴BC2+CD2=BD2
∴△BCD为直角三角形.
解法二:过点D作DF⊥y轴于点F.
在Rt△BOC中,∵OB=3,OC=3
∴OB=OC∴∠OCB=45°
∵在Rt△CDF中,DF=1,CF=OF﹣OC=4﹣3=1
∴DF=CF
∴∠DCF=45°
∴∠BCD=180°﹣∠DCF﹣∠OCB=90°
∴△BCD为直角三角形.
(3)①△BCD的三边,==,又=,故当P是原点O时,△ACP∽△DBC;
②当AC是直角边时,若AC与CD是对应边,设P的坐标是(0,a),则PC=3﹣a,=,即=,解得:a=﹣9,则P的坐标是(0,﹣9),三角形ACP不是直角三角形,则△ACP∽△CBD不成立;
③当AC是直角边,若AC与BC是对应边时,设P的坐标是(0,b),则PC=3﹣b,则=,即=,解得:b=﹣,故P是(0,﹣)时,则△ACP∽△CBD一定成立;
④当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(d,0).
则AP=1﹣d,当AC与CD是对应边时,=,即=,解得:d=1﹣3,此时,两个三角形不相似;
⑤当P在x轴上时,AC是直角边,P一定在B的左侧,设P的坐标是(e,0).
则AP=1﹣e,当AC与DC是对应边时,=,即=,解得:e=﹣9,符合条件.
总之,符合条件的点P的坐标为:.
同课章节目录
