5.4.2 第2课时 正弦函数、余弦函数的性质课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共30张PPT)
文档属性
| 名称 | 5.4.2 第2课时 正弦函数、余弦函数的性质课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共30张PPT) | 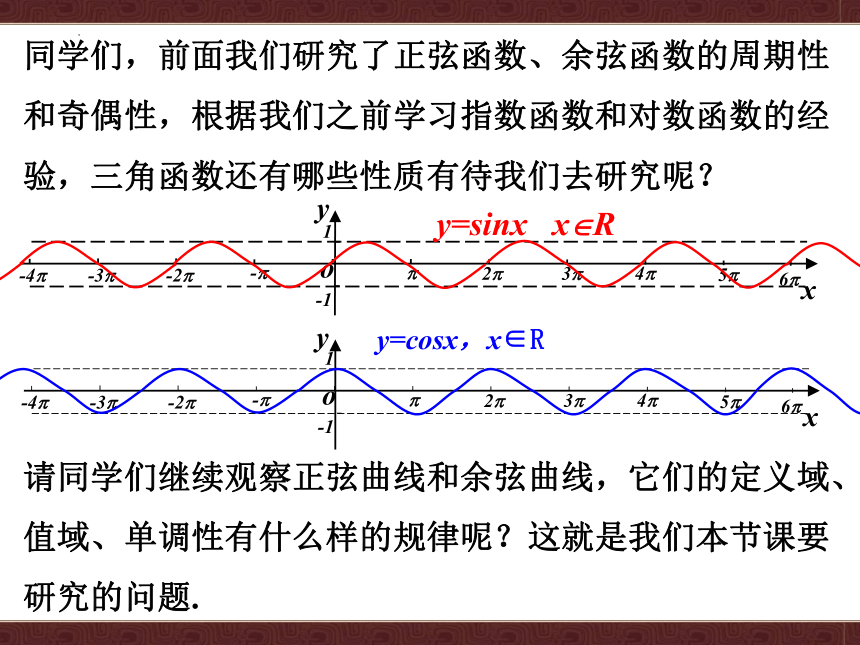 | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 10:27:55 | ||
图片预览








文档简介
同学们,前面我们研究了正弦函数、余弦函数的周期性和奇偶性,根据我们之前学习指数函数和对数函数的经验,三角函数还有哪些性质有待我们去研究呢?
请同学们继续观察正弦曲线和余弦曲线,它们的定义域、值域、单调性有什么样的规律呢?这就是我们本节课要研究的问题.
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
正、余弦函数的图象与性质
学习目标
1.理解正弦函数、余弦函数的单调性具有周期性变化的规律,通过一个周期内的单调性进而研究在整个定义域上的性质.
2.能够利用函数的单调性解决比较函数值的大小以及求函数的最值、值域等问题.
问题1:类比以往对函数性质的研究,正弦函数、余弦函数的还有哪些性质?
有单调性、最值等性质
追问:大家观察????=????????????????,????∈?????2,3????2的图像,函数值有什么特点?
?
当????∈?????2,????2时,曲线逐渐上升, ????=????????????????是增函数, ????????????????的值由-1增大到1,当????∈????2,3????2 时,曲线逐渐下降, ????=????????????????是减函数,????????????????的值由1减小到-1.
?
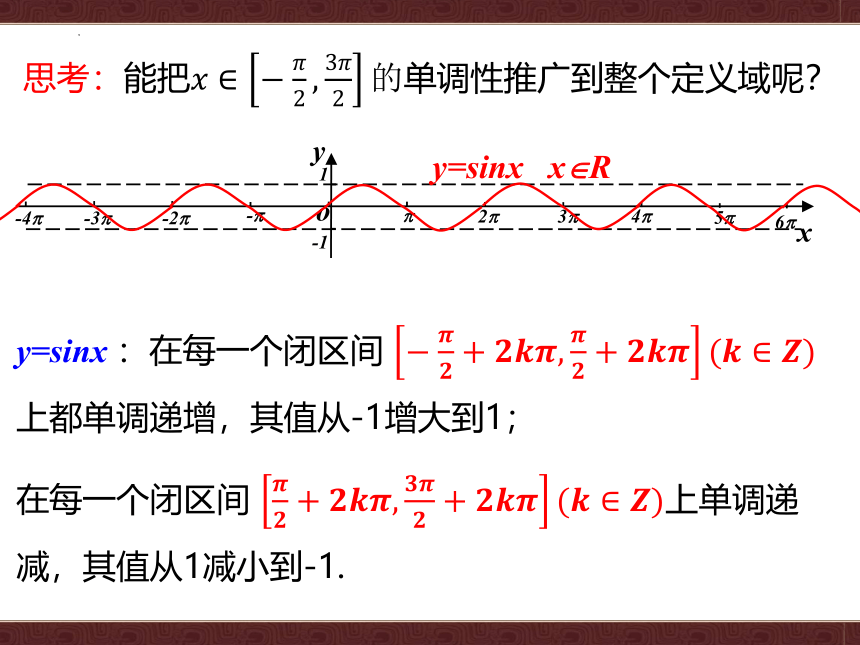
思考:能把????∈?????2,3????2的单调性推广到整个定义域呢?
?
y=sinx :在每一个闭区间 ?????????+????????????,????????+????????????(????∈????)上都单调递增,其值从-1增大到1;
在每一个闭区间 ????????+????????????,????????????+????????????(????∈????)上单调递减,其值从1减小到-1.
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
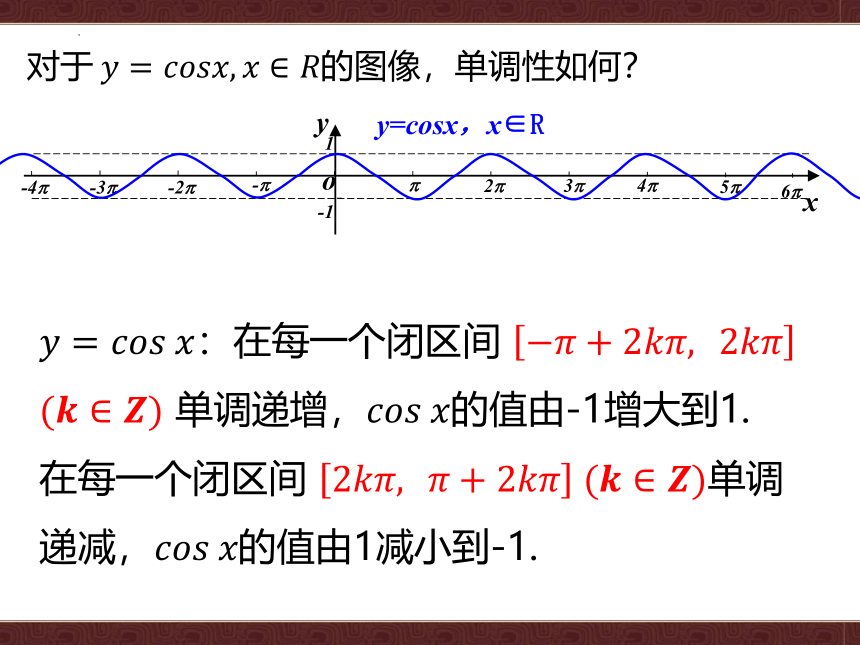
????=?????????????????:在每一个闭区间 ?????+2????????,??2???????? (????∈????) 单调递增,?????????????????的值由-1增大到1.
在每一个闭区间 2????????,??????+2???????? (????∈????)单调递减,?????????????????的值由1减小到-1.
?
对于?????=????????????????,????∈????的图像,单调性如何?
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
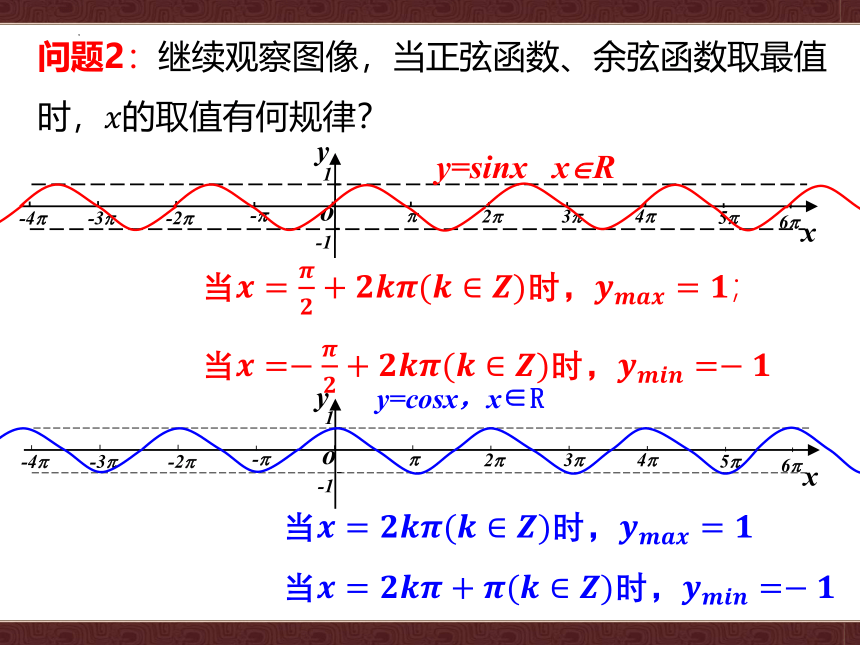
问题2:继续观察图像,当正弦函数、余弦函数取最值时,????的取值有何规律?
?
当????=????????+????????????(????∈????)时,????????????????=????;
当????=?????????+????????????(????∈????)时,????????????????=?????
?
当????=????????????(????∈????)时,????????????????=????
当????=????????????+????(????∈????)时,????????????????=?????
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
问题3:继续观察图像,正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
正弦曲线关于点( ?????????,0) (????∈????)和直线????=????????+????????(????∈????) 对称.
?
余弦曲线关于点(????????+????????,????)(????∈????) 和直线 x= ???????? (????∈????)对称.
?
继续观察相邻对称轴(或对称中心)的距离是
继续观察相邻对称轴和对称中心的距离是
????????
?
????????
?
观察对称轴(或对称中心)的正(余)弦值有什么特点?
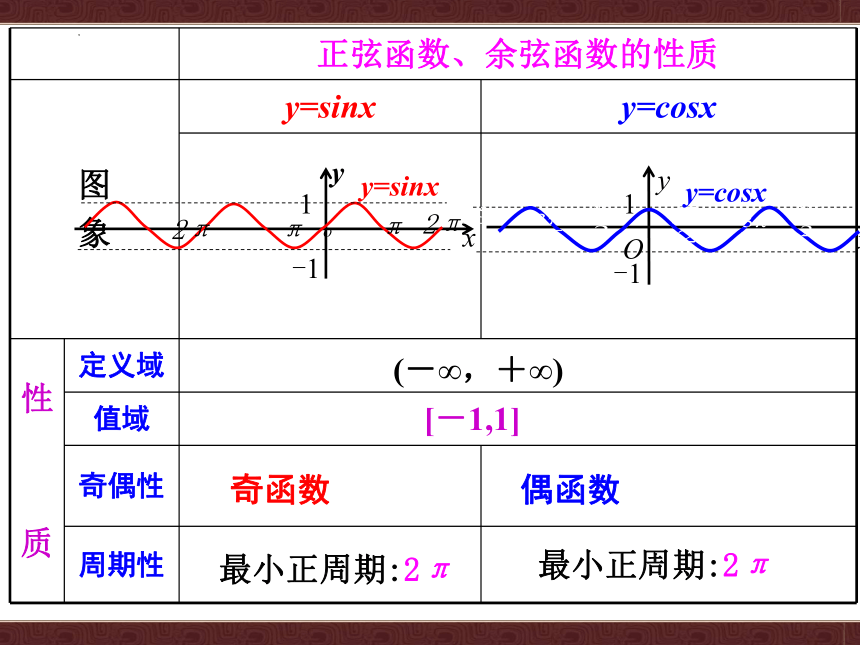
正弦函数、余弦函数的性质
图
象
y=sinx
y=cosx
性
质
定义域
值域
奇偶性
周期性
(-∞,+∞)
[-1,1]
奇函数
偶函数
最小正周期:2π
最小正周期:2π
x
y
-1
O
1
π
2π
-2π
-π
y=sinx
x
y
O
1
-1
y=cosx
性
质
单调性
最值
对称性
在?????????+????????????,????????+????????????(????∈????)上单调递增;
在????????+????????????,????????????+????????????(????∈????)上单调递减
?
在[-π+2kπ, 2kπ]
(k∈Z)上单调递增;
在[2kπ,π+2kπ]
(k∈Z)上单调递减
当????=????????+????????????(????∈????)时,
ymax=1;
当????=?????????+????????????(????∈????)时,
ymin=-1。
?
当x=2kπ (k∈Z) 时,ymax=1;
当x=π+2kπ(k∈Z) 时,ymin=-1。
对称中心:(kπ,0) (k∈Z)
对称轴:????=????????+????????(????∈????)
?
对称中心:(????????+????????,????)(????∈????)
对称轴: x= ???????? (????∈????)
?
图
象
y=sinx
y=cosx
x
y
-1
O
1
π
2π
-2π
-π
y=sinx
x
y
O
1
-1
y=cosx
利用单调性比较大小
性质应用
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
例4 不通过求值,比较下列各数的大小:
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
(1) ;
(2) .
例4 不通过求值,比较下列各数的大小:
比较三角函数值大小的步骤
(1)异名函数化为同名函数.
(2)利用诱导公式把已知角转化到同一单调区间上.
(3)利用函数的单调性比较大小.
反思感悟
(1)cos 1,sin 1;
跟踪训练1
(2)sin 164°与cos 110°.
cos 110° (3)下列关系式中正确的是
A.sin 11°B.sin 168°C.sin 11°D.sin 168°√
(4)已知α,β为锐角三角形的两个内角,则以下结论正确的是
A.sin αC.cos αcos β
√
求正弦函数、余弦函数的单调区间
解:
例5 求函数 的单调递增区间.
由?????????????????????≤????????????+????????≤????????????+????????(????∈????)解得
?????????????????????????≤????≤????????????+????????(k∈Z)
又?????????≤????≤????????,
∴?????????????≤????≤????????。
?
∴所求的单调递增区间为[?????????????,????????]
?
整体代换
求函数 的单调递增区间。
思考:
解:
由????????????+????????≤?????????????????????≤????????????+????????????(????∈????)解得
????????????+????????????≤????≤????????????+????????????????(k∈Z)
又?????????≤????≤????????,
∴?????????≤????≤?????????或∴????????????≤????≤????????.
?
∴所求的单调递增区间为[?????????,?????????],[????????????,????????]
?
整体代换
求函数 的单调递增区间。
思考:
????=?????????????????????????????????=??????????????????????????????????
?
复合法的应用
反思感悟
求正弦、余弦函数的单调区间的策略
(1)结合正、余弦函数的图象,熟记它们的单调区间.
(2)在求形如y=Asin(ωx+φ)(其中A,ω,φ为常数,且A≠0,ω>0)的函数的单调区间时,应采用“换元法”整体代换,将“ωx+φ”看作一个整体“z”,即通过求y=Asin z的单调区间而求出原函数的单调区间.求形如y=Acos(ωx+φ)(其中A,ω,φ为常数,且A≠0,ω>0)的函数的单调区间时,同上.
同时注意单调性复合法的应用
跟踪训练2
整体代换
正弦函数、余弦函数的最值(值域)
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
这两个函数都有最大值、最小值.
(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合
使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合
函数 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
(2)令t=2x,因为使函数 取最大值的t的集合是
所以使函数 取最大值的x的集合是
同理,使函数 取最小值的x的集合是
函数 取最大值是3,最小值是-3。
整体代换
反思感悟
三角函数的值域(最值)问题的求解方法
(1)形如y=Asin x(或y=Acos x)型,可利用正弦函数、余弦函数的有界性,注意对A正、负的讨论.
(2)形如y=Asin(ωx+φ)+b(或y=Acos(ωx+φ)+b)型,可先由定义域求得ωx+φ的范围,然后利用三角函数性质求得sin(ωx+φ)(或cos(ωx+φ))的范围,最后求得值域(最值).
√
跟踪训练3
∴?12≤cos(????+????6)≤32
?
解三角不等式
x
y
O
2π
π
1
-1
例 当x∈[0,2π]时,求不等式??cos????≥12 的解集.
?
若改成:cos????≥12,????∈???? 呢?
?
x
y
O
1
-1
y=cosx
画图原则,能连不散
????,????????∪[????????????,????????]
?
练习
求下列函数 的定义域;
由????>????????+????????????????????????????????????????????≥????≥????得,
????解得????所以定义域为????,????????∪[????????????,????].
?
由?????????????????????????≥?????????????????????????????>????得????????????????≤????????????????????????>????????,
????????????+????????≤????≤????????????+????????????????????????+????????解得????????????+????????≤????所以定义域为:
[????????????+????????,????????????+????????????)????∈????.
?
课堂
小结
1.知识清单:
(1)正弦、余弦函数的单调区间.
(2)比较三角函数值的大小.
(3)正弦、余弦函数的最值(值域).
2.方法归纳:整体代换、换元法.
3.常见误区:单调区间漏写k∈Z;求值域时忽视sin x,cos x本身具有的范围.
请同学们继续观察正弦曲线和余弦曲线,它们的定义域、值域、单调性有什么样的规律呢?这就是我们本节课要研究的问题.
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
正、余弦函数的图象与性质
学习目标
1.理解正弦函数、余弦函数的单调性具有周期性变化的规律,通过一个周期内的单调性进而研究在整个定义域上的性质.
2.能够利用函数的单调性解决比较函数值的大小以及求函数的最值、值域等问题.
问题1:类比以往对函数性质的研究,正弦函数、余弦函数的还有哪些性质?
有单调性、最值等性质
追问:大家观察????=????????????????,????∈?????2,3????2的图像,函数值有什么特点?
?
当????∈?????2,????2时,曲线逐渐上升, ????=????????????????是增函数, ????????????????的值由-1增大到1,当????∈????2,3????2 时,曲线逐渐下降, ????=????????????????是减函数,????????????????的值由1减小到-1.
?
思考:能把????∈?????2,3????2的单调性推广到整个定义域呢?
?
y=sinx :在每一个闭区间 ?????????+????????????,????????+????????????(????∈????)上都单调递增,其值从-1增大到1;
在每一个闭区间 ????????+????????????,????????????+????????????(????∈????)上单调递减,其值从1减小到-1.
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
????=?????????????????:在每一个闭区间 ?????+2????????,??2???????? (????∈????) 单调递增,?????????????????的值由-1增大到1.
在每一个闭区间 2????????,??????+2???????? (????∈????)单调递减,?????????????????的值由1减小到-1.
?
对于?????=????????????????,????∈????的图像,单调性如何?
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
问题2:继续观察图像,当正弦函数、余弦函数取最值时,????的取值有何规律?
?
当????=????????+????????????(????∈????)时,????????????????=????;
当????=?????????+????????????(????∈????)时,????????????????=?????
?
当????=????????????(????∈????)时,????????????????=????
当????=????????????+????(????∈????)时,????????????????=?????
?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
问题3:继续观察图像,正弦曲线除了关于原点对称外,是否还关于其它的点和直线对称?
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?R
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx,x∈R
正弦曲线关于点( ?????????,0) (????∈????)和直线????=????????+????????(????∈????) 对称.
?
余弦曲线关于点(????????+????????,????)(????∈????) 和直线 x= ???????? (????∈????)对称.
?
继续观察相邻对称轴(或对称中心)的距离是
继续观察相邻对称轴和对称中心的距离是
????????
?
????????
?
观察对称轴(或对称中心)的正(余)弦值有什么特点?
正弦函数、余弦函数的性质
图
象
y=sinx
y=cosx
性
质
定义域
值域
奇偶性
周期性
(-∞,+∞)
[-1,1]
奇函数
偶函数
最小正周期:2π
最小正周期:2π
x
y
-1
O
1
π
2π
-2π
-π
y=sinx
x
y
O
1
-1
y=cosx
性
质
单调性
最值
对称性
在?????????+????????????,????????+????????????(????∈????)上单调递增;
在????????+????????????,????????????+????????????(????∈????)上单调递减
?
在[-π+2kπ, 2kπ]
(k∈Z)上单调递增;
在[2kπ,π+2kπ]
(k∈Z)上单调递减
当????=????????+????????????(????∈????)时,
ymax=1;
当????=?????????+????????????(????∈????)时,
ymin=-1。
?
当x=2kπ (k∈Z) 时,ymax=1;
当x=π+2kπ(k∈Z) 时,ymin=-1。
对称中心:(kπ,0) (k∈Z)
对称轴:????=????????+????????(????∈????)
?
对称中心:(????????+????????,????)(????∈????)
对称轴: x= ???????? (????∈????)
?
图
象
y=sinx
y=cosx
x
y
-1
O
1
π
2π
-2π
-π
y=sinx
x
y
O
1
-1
y=cosx
利用单调性比较大小
性质应用
(1) ;
(2) .
解:(1)因为 ,
正弦函数y=sinx在区间 上单调递增,
所以
例4 不通过求值,比较下列各数的大小:
解:(2) ,
且余弦函数在区间[0,π]上单调递减,
所以
(1) ;
(2) .
例4 不通过求值,比较下列各数的大小:
比较三角函数值大小的步骤
(1)异名函数化为同名函数.
(2)利用诱导公式把已知角转化到同一单调区间上.
(3)利用函数的单调性比较大小.
反思感悟
(1)cos 1,sin 1;
跟踪训练1
(2)sin 164°与cos 110°.
cos 110°
A.sin 11°
(4)已知α,β为锐角三角形的两个内角,则以下结论正确的是
A.sin α
√
求正弦函数、余弦函数的单调区间
解:
例5 求函数 的单调递增区间.
由?????????????????????≤????????????+????????≤????????????+????????(????∈????)解得
?????????????????????????≤????≤????????????+????????(k∈Z)
又?????????≤????≤????????,
∴?????????????≤????≤????????。
?
∴所求的单调递增区间为[?????????????,????????]
?
整体代换
求函数 的单调递增区间。
思考:
解:
由????????????+????????≤?????????????????????≤????????????+????????????(????∈????)解得
????????????+????????????≤????≤????????????+????????????????(k∈Z)
又?????????≤????≤????????,
∴?????????≤????≤?????????或∴????????????≤????≤????????.
?
∴所求的单调递增区间为[?????????,?????????],[????????????,????????]
?
整体代换
求函数 的单调递增区间。
思考:
????=?????????????????????????????????=??????????????????????????????????
?
复合法的应用
反思感悟
求正弦、余弦函数的单调区间的策略
(1)结合正、余弦函数的图象,熟记它们的单调区间.
(2)在求形如y=Asin(ωx+φ)(其中A,ω,φ为常数,且A≠0,ω>0)的函数的单调区间时,应采用“换元法”整体代换,将“ωx+φ”看作一个整体“z”,即通过求y=Asin z的单调区间而求出原函数的单调区间.求形如y=Acos(ωx+φ)(其中A,ω,φ为常数,且A≠0,ω>0)的函数的单调区间时,同上.
同时注意单调性复合法的应用
跟踪训练2
整体代换
正弦函数、余弦函数的最值(值域)
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
这两个函数都有最大值、最小值.
(1)使函数 取得最大值的x的集合,就是使函数 取得最大值的x的集合
使函数 取得最小值的x的集合,就是
使函数 取得最小值的x的集合
函数 的最大值是1+1=2;最小值是
-1+1=0.
例3.下列函数有最大、最小值吗?如果有,请写出取最大、最小值时的自变量x的集合,并说出最大、最小值分别是什么.
解:
(2)令t=2x,因为使函数 取最大值的t的集合是
所以使函数 取最大值的x的集合是
同理,使函数 取最小值的x的集合是
函数 取最大值是3,最小值是-3。
整体代换
反思感悟
三角函数的值域(最值)问题的求解方法
(1)形如y=Asin x(或y=Acos x)型,可利用正弦函数、余弦函数的有界性,注意对A正、负的讨论.
(2)形如y=Asin(ωx+φ)+b(或y=Acos(ωx+φ)+b)型,可先由定义域求得ωx+φ的范围,然后利用三角函数性质求得sin(ωx+φ)(或cos(ωx+φ))的范围,最后求得值域(最值).
√
跟踪训练3
∴?12≤cos(????+????6)≤32
?
解三角不等式
x
y
O
2π
π
1
-1
例 当x∈[0,2π]时,求不等式??cos????≥12 的解集.
?
若改成:cos????≥12,????∈???? 呢?
?
x
y
O
1
-1
y=cosx
画图原则,能连不散
????,????????∪[????????????,????????]
?
练习
求下列函数 的定义域;
由????>????????+????????????????????????????????????????????≥????≥????得,
????解得????所以定义域为????,????????∪[????????????,????].
?
由?????????????????????????≥?????????????????????????????>????得????????????????≤????????????????????????>????????,
????????????+????????≤????≤????????????+????????????????????????+????????解得????????????+????????≤????所以定义域为:
[????????????+????????,????????????+????????????)????∈????.
?
课堂
小结
1.知识清单:
(1)正弦、余弦函数的单调区间.
(2)比较三角函数值的大小.
(3)正弦、余弦函数的最值(值域).
2.方法归纳:整体代换、换元法.
3.常见误区:单调区间漏写k∈Z;求值域时忽视sin x,cos x本身具有的范围.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
