5.2.1三角函数的概念 课件——2022-2023学年高一上学期数学人教A版(2019)必修第一册(共19张PPT)
文档属性
| 名称 | 5.2.1三角函数的概念 课件——2022-2023学年高一上学期数学人教A版(2019)必修第一册(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 10:31:38 | ||
图片预览






文档简介
①.与?????????终边相同的角可以表示为????=????????+????·?????????????或????=?????????+????????????吗?
?
课前练
②????????????????与?????相等吗?
?
④公式:????=________
?
????????
?
推论:________________
????扇形=_________________
?
≈0.01745 rad
③ 1?=______????????????;1????????????=________?
?
180????
?
????180
?
????=|α|r
?
????????????????=????????????????????
?
课前练
5.2.1 三角函数的概念
学习目标
1.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义.
2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号.
3.掌握公式一并会应用.
函数是描述客观变化规律的重要数学模型之一。
周而复始
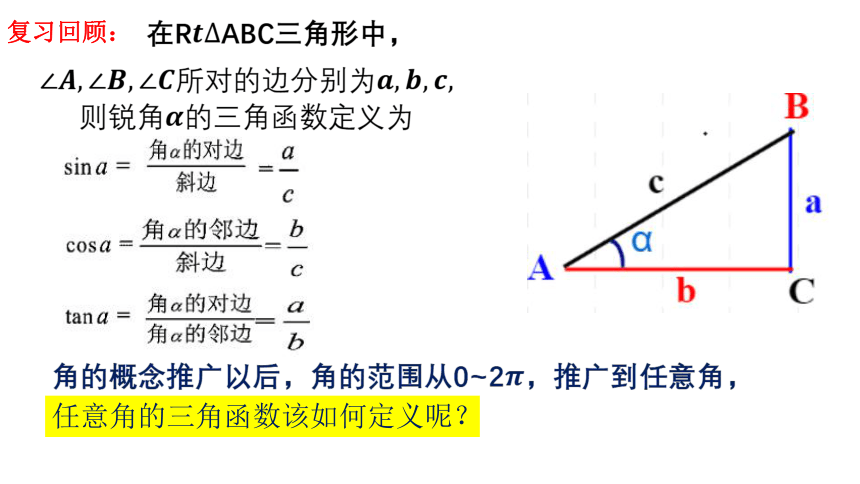
复习回顾:
在R?????ABC三角形中,
?
角的概念推广以后,角的范围从0~2????,推广到任意角,
?
∠????,∠????,∠????所对的边分别为????,????,????,则锐角????的三角函数定义为
?
任意角的三角函数该如何定义呢?
创设情境,引入新课
下面我们在单位圆中来描述圆周上点的位置变化情况。
如图,设点P以点A为起点做逆时针方向旋转
A
P
O
思考1:如何确定点P的位置?
α
易知,点P的位置由角射线OP旋转所形成的角 确定
α
在引入角的弧度制时,我们引用了单位圆,这里,为了研究问题的方便,我们依然以单位圆(半径为1的圆)为例,展开研究
(1,0)
(x,y)
x
为了建立函数模型,我们需要建立平面直角坐标系
这样,就把该问题抽象为一个质点
从点A开始在单位圆上的运动.
问题:如何确定点P的位置?
单位圆
y
思考2:建立坐标系以后,我们还能用什么详细刻画点P的位置?
P点的坐标
思考3: 你能将P点的坐标用角????表示出来吗 ?
?
探究
A(1,0)
P (x, y)
O
x
M
y
如图,设P(x, y)是α的终边OP与单位圆的交点
则
|????????|=____
?
1
????=????????时,????的坐标为_____;
?
????=????????时,????的坐标为_____;
?
????=????????????时,????的坐标为_____;
?
显然,????确定时,P的坐标也是唯一确定的。
?
????????,????????
?
????,????
?
?????????,?????????
?
这里面存在两个函数关系:
(1)点P的纵坐标y是关于α的函数;
(2)点P的横坐标x是关于α的函数;
探究
A(1,0)
P (x, y)
O
x
α
M
y
如图,设P(x, y)是α的终边OP与单位圆的交点
则
|????????|=____
?
1
????????????????=
?
????????????????=
?
????????????????=
?
????????????????
?
=????????=
?
????????????????
?
=????????=
?
????????????????=
?
????????(????≠0)
?
????
?
????
?
????(????,????)=????(????????????????,????????????????
?
事实上,任意给定一个角????∈????,它的终边OP与单位圆交点P的坐标(????,????)都是唯一确定的。
?
课本177页
点P的横坐标x叫做α的余弦函数
点P的纵坐标y叫做α的正弦函数
点P的纵坐标和横坐标的比值????????叫做????的正切函数
?
通常按照习惯,用x表示自变量,用y表示函数
y=sinx ,
y=tanx ,
y=cosx,
????=????????????????
?
????=????????????????
?
????????=????????????????
?
余弦函数
正弦函数
正切函数
我们将正弦函数、余弦函数和正切函数统称为三角函数,
三角函数第一定义(单位圆定义)
x∈R
?
x∈R
?
????≠????2+k??????(????∈????)
?
这三个三角函数的定义域是怎样的?
(????≠0)
?
????终边不在y轴
?
①把角放在平面直角坐标系中;
②构造直角三角形;
③求出角的终边与单位圆的交点坐标;
④利用定义来确定三角函数的值;
例1 求 的正弦值、余弦值和正切值.
?
?
?
?
?
?
【解】在坐标系中作出∠AOB= ,易知∠AOB的终边与单位圆的交点P的坐标为 ,所以
?
?
思考:若把角 改为 呢?
探究
P (x, y)
O
x
α
M
y
如图,设P(x, y)是α的终边OP与任意半径为r的圆的交点
则
????????=______________
?
????????????????=
?
????????????????=
?
????????????????=
?
????????????????
?
????????????????
?
????????????????
?
=????????
?
=????????
?
=????????
?
????
?
=????????+????????
?
课本179页例2
三角函数第二定义
于是,
例2 、已知角 的终边过点 ,求 的三个三角函数值.
解:由已知可得:
【例3】
常见角的三角函数值
?
?
?
?
?
?
?
?
?
?
?
?
?
?
无
?
?
?
?
?
?
?
?
?
牢记常见的三角函数值,做题事半功倍!
三角函数的定义域和函数值的符号
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
[-1,1]
[-1,1]
一全正、二正弦、三正切、四余弦
全(+)是(s)天(t)才(c)
诱导公式一
由三角函数的定义,我们知道:终边相同的角的同一三角函数的值相等.
?
公式一:
其中k∈Z
【问题】公式一说明了角和三角函数值的什么关系?给我们什么启发?
【答】公式一说明了角和三角函数值的对应关系是多角对一值的关系:
即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对因.
课堂小结
任意角的三角函数
借助单位圆定义
求角的三角函数值
作业:
1.整理笔记
2.完成课本184页第2题,分层(42)黄皮136页A组删6.9;
3.有疑问的题目
?
课前练
②????????????????与?????相等吗?
?
④公式:????=________
?
????????
?
推论:________________
????扇形=_________________
?
≈0.01745 rad
③ 1?=______????????????;1????????????=________?
?
180????
?
????180
?
????=|α|r
?
????????????????=????????????????????
?
课前练
5.2.1 三角函数的概念
学习目标
1.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义.
2.掌握任意角三角函数(正弦、余弦、正切)在各象限的符号.
3.掌握公式一并会应用.
函数是描述客观变化规律的重要数学模型之一。
周而复始
复习回顾:
在R?????ABC三角形中,
?
角的概念推广以后,角的范围从0~2????,推广到任意角,
?
∠????,∠????,∠????所对的边分别为????,????,????,则锐角????的三角函数定义为
?
任意角的三角函数该如何定义呢?
创设情境,引入新课
下面我们在单位圆中来描述圆周上点的位置变化情况。
如图,设点P以点A为起点做逆时针方向旋转
A
P
O
思考1:如何确定点P的位置?
α
易知,点P的位置由角射线OP旋转所形成的角 确定
α
在引入角的弧度制时,我们引用了单位圆,这里,为了研究问题的方便,我们依然以单位圆(半径为1的圆)为例,展开研究
(1,0)
(x,y)
x
为了建立函数模型,我们需要建立平面直角坐标系
这样,就把该问题抽象为一个质点
从点A开始在单位圆上的运动.
问题:如何确定点P的位置?
单位圆
y
思考2:建立坐标系以后,我们还能用什么详细刻画点P的位置?
P点的坐标
思考3: 你能将P点的坐标用角????表示出来吗 ?
?
探究
A(1,0)
P (x, y)
O
x
M
y
如图,设P(x, y)是α的终边OP与单位圆的交点
则
|????????|=____
?
1
????=????????时,????的坐标为_____;
?
????=????????时,????的坐标为_____;
?
????=????????????时,????的坐标为_____;
?
显然,????确定时,P的坐标也是唯一确定的。
?
????????,????????
?
????,????
?
?????????,?????????
?
这里面存在两个函数关系:
(1)点P的纵坐标y是关于α的函数;
(2)点P的横坐标x是关于α的函数;
探究
A(1,0)
P (x, y)
O
x
α
M
y
如图,设P(x, y)是α的终边OP与单位圆的交点
则
|????????|=____
?
1
????????????????=
?
????????????????=
?
????????????????=
?
????????????????
?
=????????=
?
????????????????
?
=????????=
?
????????????????=
?
????????(????≠0)
?
????
?
????
?
????(????,????)=????(????????????????,????????????????
?
事实上,任意给定一个角????∈????,它的终边OP与单位圆交点P的坐标(????,????)都是唯一确定的。
?
课本177页
点P的横坐标x叫做α的余弦函数
点P的纵坐标y叫做α的正弦函数
点P的纵坐标和横坐标的比值????????叫做????的正切函数
?
通常按照习惯,用x表示自变量,用y表示函数
y=sinx ,
y=tanx ,
y=cosx,
????=????????????????
?
????=????????????????
?
????????=????????????????
?
余弦函数
正弦函数
正切函数
我们将正弦函数、余弦函数和正切函数统称为三角函数,
三角函数第一定义(单位圆定义)
x∈R
?
x∈R
?
????≠????2+k??????(????∈????)
?
这三个三角函数的定义域是怎样的?
(????≠0)
?
????终边不在y轴
?
①把角放在平面直角坐标系中;
②构造直角三角形;
③求出角的终边与单位圆的交点坐标;
④利用定义来确定三角函数的值;
例1 求 的正弦值、余弦值和正切值.
?
?
?
?
?
?
【解】在坐标系中作出∠AOB= ,易知∠AOB的终边与单位圆的交点P的坐标为 ,所以
?
?
思考:若把角 改为 呢?
探究
P (x, y)
O
x
α
M
y
如图,设P(x, y)是α的终边OP与任意半径为r的圆的交点
则
????????=______________
?
????????????????=
?
????????????????=
?
????????????????=
?
????????????????
?
????????????????
?
????????????????
?
=????????
?
=????????
?
=????????
?
????
?
=????????+????????
?
课本179页例2
三角函数第二定义
于是,
例2 、已知角 的终边过点 ,求 的三个三角函数值.
解:由已知可得:
【例3】
常见角的三角函数值
?
?
?
?
?
?
?
?
?
?
?
?
?
?
无
?
?
?
?
?
?
?
?
?
牢记常见的三角函数值,做题事半功倍!
三角函数的定义域和函数值的符号
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
[-1,1]
[-1,1]
一全正、二正弦、三正切、四余弦
全(+)是(s)天(t)才(c)
诱导公式一
由三角函数的定义,我们知道:终边相同的角的同一三角函数的值相等.
?
公式一:
其中k∈Z
【问题】公式一说明了角和三角函数值的什么关系?给我们什么启发?
【答】公式一说明了角和三角函数值的对应关系是多角对一值的关系:
即给定一个角,它的三角函数值只要存在,就是唯一的;
反过来,给定一个三角函数值,却有无数个角与之对因.
课堂小结
任意角的三角函数
借助单位圆定义
求角的三角函数值
作业:
1.整理笔记
2.完成课本184页第2题,分层(42)黄皮136页A组删6.9;
3.有疑问的题目
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
