5.4.1正弦函数、余弦函数的图象课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共17张PPT)
文档属性
| 名称 | 5.4.1正弦函数、余弦函数的图象课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 10:34:55 | ||
图片预览









文档简介
一物体做匀速直线运动的位移s与时间t之间的关系可以用一次函数来刻画;它做匀变速直线运动的位移s与时间t之间的关系可以用二次函数来刻画
很多自然现象都可以通过函数来刻画其本质……
四季变化
围绕其他行星公转
从前面的学习中我们已经看到三角函数具有“周而复始”的变化规律
同学们,我国著名数学家华罗庚教授写过这样一首诗:“数与形,本是相倚依,焉能分作两边飞.数无形时少直觉,形少数时难入微.数形结合百般好,隔离分家万事非;切莫忘,几何代数统一体,永远联系,切莫分离”诗中充分肯定了数形结合这一重要的数学思想方法,前面我们主要从“数”的角度研究了三角函数的一些问题,这节课我们将从“形”上来研究三角函数.
正、余弦函数的图象
学习目标
1.理解正弦曲线和余弦曲线间的关系,会用“五点(画图)法”画给定区间上的正弦函数、余弦函数的图象.
2.掌握正弦函数与余弦函数图象间的关系以及图象的变换,能通过函数图象解决简单的问题.
我们知道,单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式????????????(????±????????)=?????????????????,????????????(????±????????)=?????????????????来表示.这说明,自变量每增加(减少)????????,正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
?
下面先研究函数????=?????????????????,????∈????的图象,从画函数????=?????????????????,????∈[????,????????]的图象开始.
?
在[0,2π]上取一个值x0,如何利用正弦函数的定义,确定正弦函数值sinx0,并画出点T(x0,sinx0)?
如图,在直角坐标系中画出以原点????为圆心的单位圆⊙????,与????轴正半轴的交点为????(????,????).在单位圆上,将点????绕着点????旋转????????弧度至点????,
根据正弦函数的定义,点????的纵坐标????????=?????????????????????.
由此,以????????为横坐标,????????为纵坐标画点,
即得到函数图象上的点????(????????,?????????????????????).
?
????
?
????????
?
????(????????,?????????????????????)
?
O
y
x
????????
?
????????
?
????
?
????
?
O
y
x
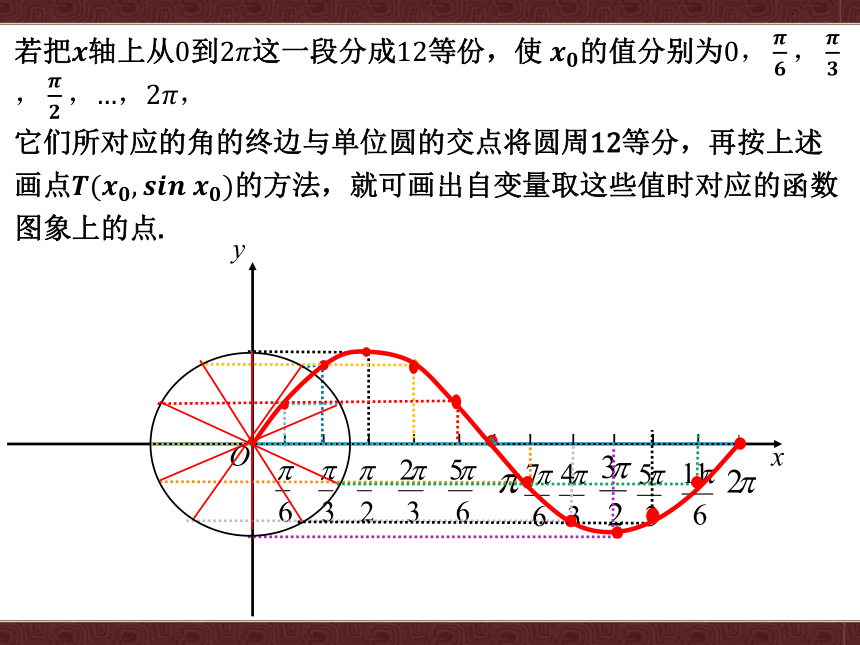
若把????轴上从0到2????这一段分成12等份,使?????????的值分别为0,????????,????????,????????,…,2????,
它们所对应的角的终边与单位圆的交点将圆周12等分,再按上述画点????(????????,?????????????????????)的方法,就可画出自变量取这些值时对应的函数图象上的点.
?
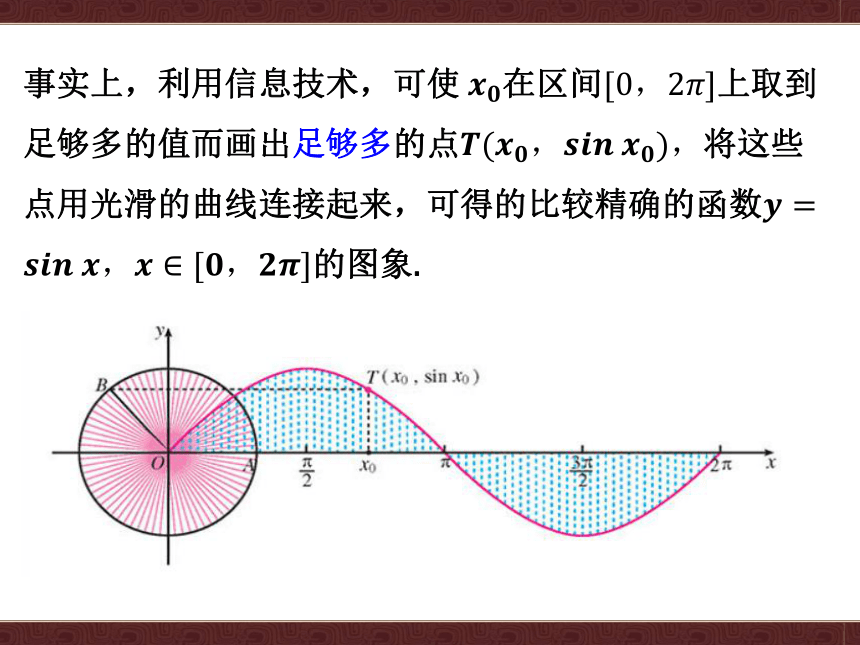
事实上,利用信息技术,可使?????????在区间[0,2????]上取到足够多的值而画出足够多的点????(????????,?????????????????????),将这些点用光滑的曲线连接起来,可得的比较精确的函数????=?????????????????,????∈[????,????????]的图象.
?
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?[0,2?]
y=sinx x?R
正弦曲线
y
x
o
1
-1
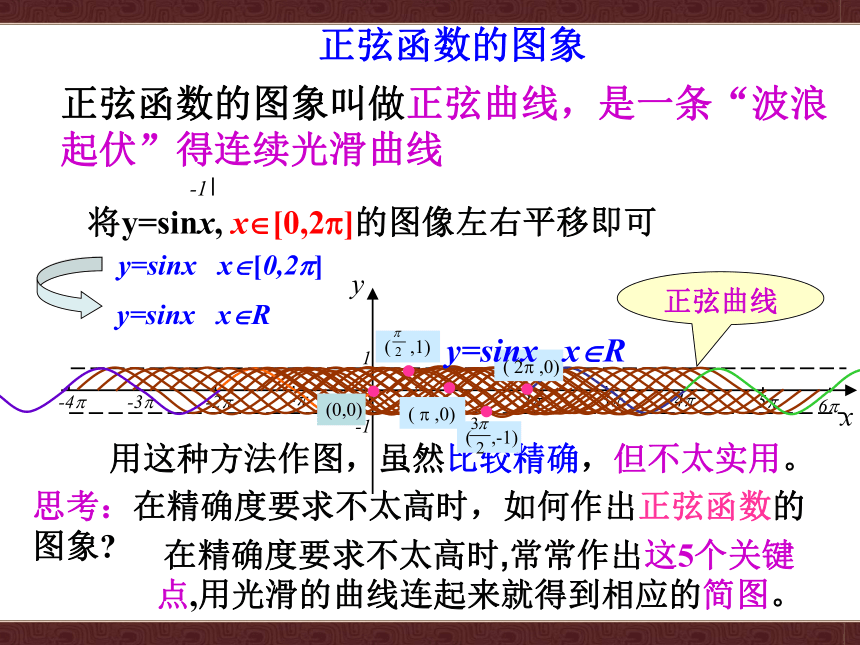
将y=sinx, x?[0,2?]的图像左右平移即可
用这种方法作图,虽然比较精确,但不太实用。
思考:在精确度要求不太高时,如何作出正弦函数的图象?
观察正弦曲线,找出起关键作用的点
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
在精确度要求不太高时,常常作出这5个关键点,用光滑的曲线连起来就得到相应的简图。
y=sinx x?R
y=sinx x?[0,2?]
正弦函数的图象叫做正弦曲线,是一条“波浪起伏”得连续光滑曲线
五点画图法
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
“五点法”画函数y=sinx在[0,2π]内的图象
y
x
o
1
-1
①列表
②描五点
③用光滑的曲线连接起来
“五点法”只画y=sinx在[0,2π]内的图象,要画在R内的图像,需要再左右平移即可
y=sinx x?[0,2?]
思考:你认为应该利用正弦函数和余弦函数的哪些关系,通过怎样的图形变换,才能将正弦函数的图象变换为余弦函数?
对于函数????=?????????????????,由诱导公式?????????????????=????????????(????+????????)得,????=?????????????????=????????????(????+????????),????∈????.
而函数????=????????????(????+????????)的图象可以通过正弦函数????=?????????????????,????∈????的图象向左平移????????个单位长度而得到.所以,将正弦函数的图象向左平移????????个单位长度,就得到余弦函数的图象,如图所示:
?
由三角函数定义可知,正弦函数、余弦函数时一对密切关联得函数。下面我们利用这种关系,借助正函数得图象画余弦函数得图象。
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+ ), x?R
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
正弦曲线
形状完全一样只是位置不同
观察余弦曲线,找出起关键作用的点
函数y=cosx,x∈R的图象叫做余弦曲线
余弦曲线
y=cosx,x∈R
五点画图法
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
“五点法”画函数y=cosx在[0,2π]内的图象
y
x
o
1
-1
①列表
②描五点
③用光滑的曲线连接起来
“五点法”只画y=cosx在[0,2π]内的图象,要画在R内的图像,需要再左右平移即可
y=cosx x?[0,2?]
正弦函数、余弦函数图象的初步认识
一
下列叙述正确的个数为
①y=sin x,x∈[0,2π]的图象关于点P(π,0)成中心对称;
②y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称;
③正弦、余弦函数的图象不超过直线y=1和y=-1所夹的范围.
A.0 B.1 C.2 D.3
√
例1
下列关于正弦函数、余弦函数的图象的描述,不正确的是
A.都可由[0,2π]内的图象向上、向下无限延展得到
B.都是对称图形
C.都与x轴有无数个交点
D.y=sin(-x)的图象与y=sin x的图象关于x轴对称
跟踪训练1
√
“五点(画图)法”应用
二
练 你能画出y=|sin x|在[0,2????]的图像吗?
解:函数y=sin x,[0,2????]的图像如图所示
y
x
O
π
1
2π
-1
y
x
O
π
1
2π
-1
故函数y=|sinx|,[0,2????]的图像如图所示:
请同学们观察,函数y=sin x与函数y=|sin x|的图像有什么关系?
正弦函数、余弦函数图象的应用
三
不等式2sin x-1≥0,x∈[0,2π]的解集为
例3
数形结合
√
延伸探究
1.在本例中把“x∈[0,2π]”改为“x∈R”,求不等式2sin x-1≥0的解集.
反思感悟
利用三角函数图象解三角不等式sin x>a(cos x>a)的步骤:
(1)作出相应的正弦函数(余弦函数)在[0,2π]上的图象.
(2)确定在[0,2π]上sin x=a(cos x=a)的x值.
(3)写出不等式在区间[0,2π]上的解集.
(4)根据诱导公式一写出定义域内的解集.
方程x2-cos x=0的实数解的个数是___,所有的实数解的和为___.
跟踪训练3
2
0
课堂
小结
1.知识清单:
(1)正弦函数、余弦函数的图象.
(2)“五点法”作图.
(3)函数图象的应用.
2.方法归纳:数形结合.
3.常见误区:五点的选取;平移得余弦函数的图象.
很多自然现象都可以通过函数来刻画其本质……
四季变化
围绕其他行星公转
从前面的学习中我们已经看到三角函数具有“周而复始”的变化规律
同学们,我国著名数学家华罗庚教授写过这样一首诗:“数与形,本是相倚依,焉能分作两边飞.数无形时少直觉,形少数时难入微.数形结合百般好,隔离分家万事非;切莫忘,几何代数统一体,永远联系,切莫分离”诗中充分肯定了数形结合这一重要的数学思想方法,前面我们主要从“数”的角度研究了三角函数的一些问题,这节课我们将从“形”上来研究三角函数.
正、余弦函数的图象
学习目标
1.理解正弦曲线和余弦曲线间的关系,会用“五点(画图)法”画给定区间上的正弦函数、余弦函数的图象.
2.掌握正弦函数与余弦函数图象间的关系以及图象的变换,能通过函数图象解决简单的问题.
我们知道,单位圆上任意一点在圆周上旋转一周就回到原来的位置,这一现象可以用公式????????????(????±????????)=?????????????????,????????????(????±????????)=?????????????????来表示.这说明,自变量每增加(减少)????????,正弦函数值、余弦函数值将重复出现.利用这一特性,就可以简化正弦函数、余弦函数的图象与性质的研究过程.
?
下面先研究函数????=?????????????????,????∈????的图象,从画函数????=?????????????????,????∈[????,????????]的图象开始.
?
在[0,2π]上取一个值x0,如何利用正弦函数的定义,确定正弦函数值sinx0,并画出点T(x0,sinx0)?
如图,在直角坐标系中画出以原点????为圆心的单位圆⊙????,与????轴正半轴的交点为????(????,????).在单位圆上,将点????绕着点????旋转????????弧度至点????,
根据正弦函数的定义,点????的纵坐标????????=?????????????????????.
由此,以????????为横坐标,????????为纵坐标画点,
即得到函数图象上的点????(????????,?????????????????????).
?
????
?
????????
?
????(????????,?????????????????????)
?
O
y
x
????????
?
????????
?
????
?
????
?
O
y
x
若把????轴上从0到2????这一段分成12等份,使?????????的值分别为0,????????,????????,????????,…,2????,
它们所对应的角的终边与单位圆的交点将圆周12等分,再按上述画点????(????????,?????????????????????)的方法,就可画出自变量取这些值时对应的函数图象上的点.
?
事实上,利用信息技术,可使?????????在区间[0,2????]上取到足够多的值而画出足够多的点????(????????,?????????????????????),将这些点用光滑的曲线连接起来,可得的比较精确的函数????=?????????????????,????∈[????,????????]的图象.
?
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=sinx x?[0,2?]
y=sinx x?R
正弦曲线
y
x
o
1
-1
将y=sinx, x?[0,2?]的图像左右平移即可
用这种方法作图,虽然比较精确,但不太实用。
思考:在精确度要求不太高时,如何作出正弦函数的图象?
观察正弦曲线,找出起关键作用的点
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
在精确度要求不太高时,常常作出这5个关键点,用光滑的曲线连起来就得到相应的简图。
y=sinx x?R
y=sinx x?[0,2?]
正弦函数的图象叫做正弦曲线,是一条“波浪起伏”得连续光滑曲线
五点画图法
(0,0)
( ,1)
( ? ,0)
( ,-1)
( 2? ,0)
“五点法”画函数y=sinx在[0,2π]内的图象
y
x
o
1
-1
①列表
②描五点
③用光滑的曲线连接起来
“五点法”只画y=sinx在[0,2π]内的图象,要画在R内的图像,需要再左右平移即可
y=sinx x?[0,2?]
思考:你认为应该利用正弦函数和余弦函数的哪些关系,通过怎样的图形变换,才能将正弦函数的图象变换为余弦函数?
对于函数????=?????????????????,由诱导公式?????????????????=????????????(????+????????)得,????=?????????????????=????????????(????+????????),????∈????.
而函数????=????????????(????+????????)的图象可以通过正弦函数????=?????????????????,????∈????的图象向左平移????????个单位长度而得到.所以,将正弦函数的图象向左平移????????个单位长度,就得到余弦函数的图象,如图所示:
?
由三角函数定义可知,正弦函数、余弦函数时一对密切关联得函数。下面我们利用这种关系,借助正函数得图象画余弦函数得图象。
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
余弦函数的图象
正弦函数的图象
x
6?
y
o
-?
-1
2?
3?
4?
5?
-2?
-3?
-4?
1
?
y=cosx=sin(x+ ), x?R
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
正弦曲线
形状完全一样只是位置不同
观察余弦曲线,找出起关键作用的点
函数y=cosx,x∈R的图象叫做余弦曲线
余弦曲线
y=cosx,x∈R
五点画图法
(0,1)
( ,0)
( ? ,-1)
( ,0)
( 2? ,1)
“五点法”画函数y=cosx在[0,2π]内的图象
y
x
o
1
-1
①列表
②描五点
③用光滑的曲线连接起来
“五点法”只画y=cosx在[0,2π]内的图象,要画在R内的图像,需要再左右平移即可
y=cosx x?[0,2?]
正弦函数、余弦函数图象的初步认识
一
下列叙述正确的个数为
①y=sin x,x∈[0,2π]的图象关于点P(π,0)成中心对称;
②y=cos x,x∈[0,2π]的图象关于直线x=π成轴对称;
③正弦、余弦函数的图象不超过直线y=1和y=-1所夹的范围.
A.0 B.1 C.2 D.3
√
例1
下列关于正弦函数、余弦函数的图象的描述,不正确的是
A.都可由[0,2π]内的图象向上、向下无限延展得到
B.都是对称图形
C.都与x轴有无数个交点
D.y=sin(-x)的图象与y=sin x的图象关于x轴对称
跟踪训练1
√
“五点(画图)法”应用
二
练 你能画出y=|sin x|在[0,2????]的图像吗?
解:函数y=sin x,[0,2????]的图像如图所示
y
x
O
π
1
2π
-1
y
x
O
π
1
2π
-1
故函数y=|sinx|,[0,2????]的图像如图所示:
请同学们观察,函数y=sin x与函数y=|sin x|的图像有什么关系?
正弦函数、余弦函数图象的应用
三
不等式2sin x-1≥0,x∈[0,2π]的解集为
例3
数形结合
√
延伸探究
1.在本例中把“x∈[0,2π]”改为“x∈R”,求不等式2sin x-1≥0的解集.
反思感悟
利用三角函数图象解三角不等式sin x>a(cos x>a)的步骤:
(1)作出相应的正弦函数(余弦函数)在[0,2π]上的图象.
(2)确定在[0,2π]上sin x=a(cos x=a)的x值.
(3)写出不等式在区间[0,2π]上的解集.
(4)根据诱导公式一写出定义域内的解集.
方程x2-cos x=0的实数解的个数是___,所有的实数解的和为___.
跟踪训练3
2
0
课堂
小结
1.知识清单:
(1)正弦函数、余弦函数的图象.
(2)“五点法”作图.
(3)函数图象的应用.
2.方法归纳:数形结合.
3.常见误区:五点的选取;平移得余弦函数的图象.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
