5.3.2诱导公式二课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共18张PPT)
文档属性
| 名称 | 5.3.2诱导公式二课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 12:07:25 | ||
图片预览






文档简介
(共18张PPT)
回顾前面的学习,我们利用单位圆定义了三角函数,利用单位圆推出了一组神奇的公式,利用它可以把任意角的三角函数转化为锐角三角函数.
单位圆,这是一个多么美妙的图形!
它就像一轮光芒四射的太阳,照耀我们的探究之路;又像一艘轮船,引领我们在知识的海洋里航行.
这节课,我们将继续在单位圆中探寻三角函数的奥秘.
诱导公式(二)
学习目标
1.理解公式五、六的推导过程并熟记诱导公式,理解和掌握公式的内涵及结构特征.
2.会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简.
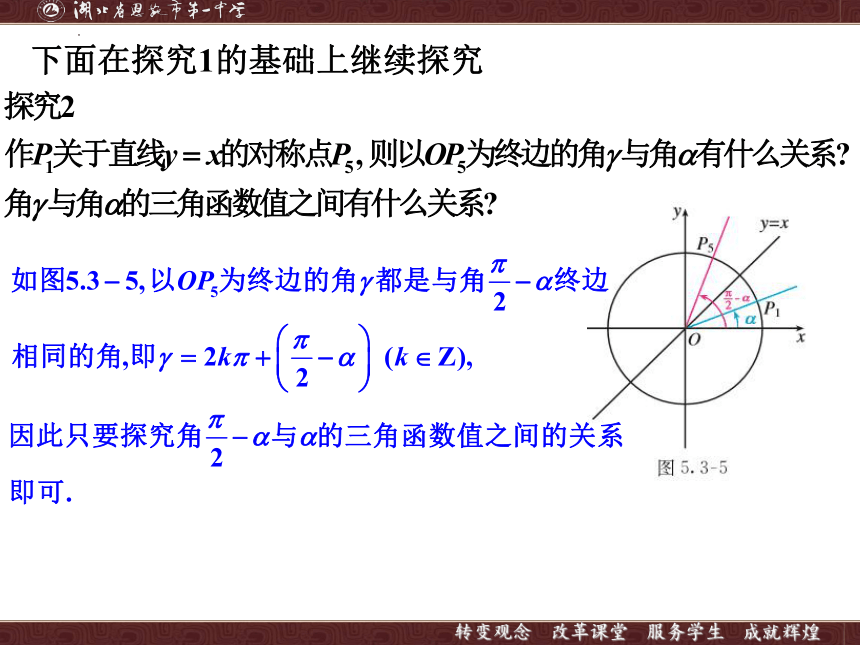
下面在探究1的基础上继续探究
公式五:
公式六:
问题1 你能概括一下公式五、六的共同特点和规律吗?
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.
利用公式五或公式六,可以实现正弦函数与余弦函数的相互转化.
函数名改变,符号看象限
公式一公式六都叫做诱导公式
问题2
(1)请大家花3分钟的时间将公式一~公式六默写下来;
(2)诱导公式可统一什么形式的角(几何形式)的三角函数与的三角函数之间的关系?
(3)你有什么办法记住这些公式?
口诀:奇变偶不变,符号看象限
(1)为奇数时,函数名改变,符号看象限。
(2)为偶数时,函数名不变,符号看象限;
例3.证明:
(1);
(2).
证明:(1)
(2)
.
化简求值
例4.化简
解:原式
=
利用诱导公式化简、求值的策略
(1)已知角求值问题,关键是利用诱导公式把任意角的三角函数值转化成锐角的三角函数值求解,转化过程中注意口诀“奇变偶不变,符号看象限”的应用.
(2)对式子进行化简或求值时,要注意要求的角与已知角之间的关系,并结合诱导公式进行转化,特别要注意角的范围.
反思感悟
f(α)=-cos α.
跟踪训练1
√
诱导公式的综合应用
例5.已知且
求的值.
解:因为+所以由诱导公式五,得:
因为,所以.
由得:
所以
所以.
反思感悟
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形,平方和差、立方和差公式.
√
跟踪训练2
课堂
小结
1.知识清单:利用诱导公式进行化简、求值与证明.
2.方法归纳:公式法、角的构造.
3.常见误区:函数符号的变化,角与角之间的联系与构造.
回顾前面的学习,我们利用单位圆定义了三角函数,利用单位圆推出了一组神奇的公式,利用它可以把任意角的三角函数转化为锐角三角函数.
单位圆,这是一个多么美妙的图形!
它就像一轮光芒四射的太阳,照耀我们的探究之路;又像一艘轮船,引领我们在知识的海洋里航行.
这节课,我们将继续在单位圆中探寻三角函数的奥秘.
诱导公式(二)
学习目标
1.理解公式五、六的推导过程并熟记诱导公式,理解和掌握公式的内涵及结构特征.
2.会初步运用诱导公式求三角函数的值,并进行简单三角函数式的化简.
下面在探究1的基础上继续探究
公式五:
公式六:
问题1 你能概括一下公式五、六的共同特点和规律吗?
的正弦(余弦)函数值,分别等于α的余弦(正弦)函数值,前面加上一个把α看成锐角时原函数值的符号.
利用公式五或公式六,可以实现正弦函数与余弦函数的相互转化.
函数名改变,符号看象限
公式一公式六都叫做诱导公式
问题2
(1)请大家花3分钟的时间将公式一~公式六默写下来;
(2)诱导公式可统一什么形式的角(几何形式)的三角函数与的三角函数之间的关系?
(3)你有什么办法记住这些公式?
口诀:奇变偶不变,符号看象限
(1)为奇数时,函数名改变,符号看象限。
(2)为偶数时,函数名不变,符号看象限;
例3.证明:
(1);
(2).
证明:(1)
(2)
.
化简求值
例4.化简
解:原式
=
利用诱导公式化简、求值的策略
(1)已知角求值问题,关键是利用诱导公式把任意角的三角函数值转化成锐角的三角函数值求解,转化过程中注意口诀“奇变偶不变,符号看象限”的应用.
(2)对式子进行化简或求值时,要注意要求的角与已知角之间的关系,并结合诱导公式进行转化,特别要注意角的范围.
反思感悟
f(α)=-cos α.
跟踪训练1
√
诱导公式的综合应用
例5.已知且
求的值.
解:因为+所以由诱导公式五,得:
因为,所以.
由得:
所以
所以.
反思感悟
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.
二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形,平方和差、立方和差公式.
√
跟踪训练2
课堂
小结
1.知识清单:利用诱导公式进行化简、求值与证明.
2.方法归纳:公式法、角的构造.
3.常见误区:函数符号的变化,角与角之间的联系与构造.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
