5.5.1 第1课时 两角差的余弦公式 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共23张PPT)
文档属性
| 名称 | 5.5.1 第1课时 两角差的余弦公式 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 12:19:55 | ||
图片预览








文档简介
(共23张PPT)
前面我们学习了诱导公式,利用它们对三角函数式进行恒等变形,可以达到化简、求值或证明的目的.这种利用公式对三角函数式进行的恒等变形就是三角恒等变换.
观察诱导公式,可以发现它们都是特殊角与任意角α的和 (或差)的三角函数与这个任意角α的三角函数的恒等关系.如
如果把特殊角换为任意角β,那么任意角α与β的和 (或差)的三角函数与α,β的三角函数会有什么关系呢?
cos(π-α)= - cosα
如怎样求cos(β-α)呢?下面来研究这个问题.
两角差的余弦公式
学习目标
1.熟悉两角差的余弦公式的推导过程.
2.掌握两角差的余弦公式的应用.
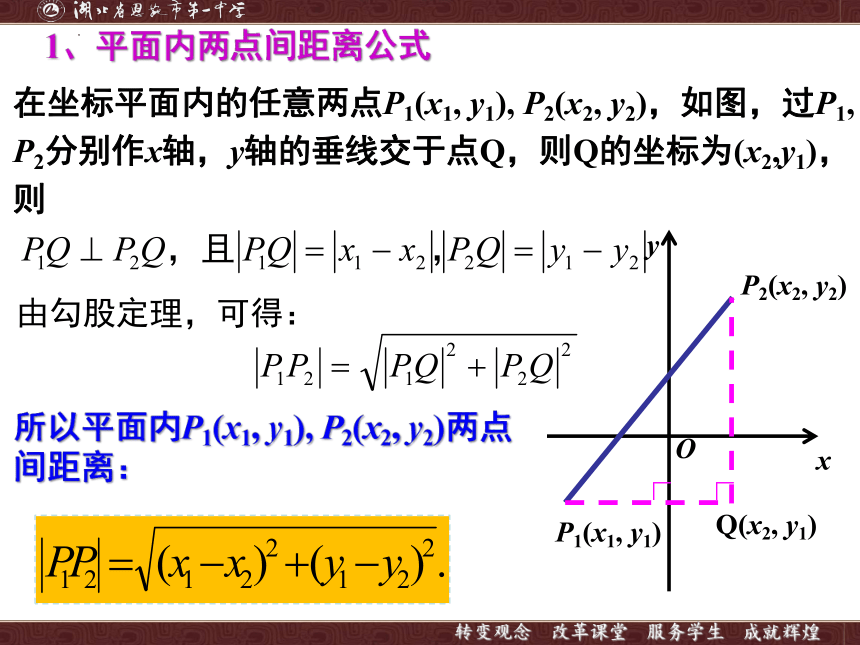
在坐标平面内的任意两点P1(x1, y1), P2(x2, y2),如图,过P1, P2分别作x轴,y轴的垂线交于点Q,则Q的坐标为(x2,y1),则
由勾股定理,可得:
所以平面内P1(x1, y1), P2(x2, y2)两点间距离:
x
y
O
P1(x1, y1)
P2(x2, y2)
Q(x2, y1)
∟
∟
1、平面内两点间距离公式
α终边
β终边
α-β终边
如图,设单位圆于x轴的正半轴相交于点A(1,0),
以x轴非负半轴为始边作角α,β ,α-β ,它们
的终边分别与单位圆相交于点P1(cosα,sinα), A1(cosβ, sinβ),P(cos(α-β), sin(α-β)).
下面我们来探究cos(α-β)角α,β的正弦、余弦之间的关系.
不妨令α≠2kπ+β,k∈Z,
如果已知任意角α,β的正弦、余弦,能由此推出α-β的正弦、余弦吗?
探究
α终边
β终边
α-β终边
连接A1P1,AP.若把扇形OAP绕着点O旋转β角,则点A,P分别与点A1,P1重合.根据圆的旋转对称性可知:
AP 与A1P1重合,从而AP = A1P1 ,所以AP = A1P1.
根据两点间的距离公式,得:
当α=2kπ+β, k∈Z时,
容易证明上式仍然成立.
[cos(α-β)-1]2+[sin(α-β)]2
=(cosα -cosβ)2 +(sinα -sinβ)2
化简得:
cos(α-β)=cosαcosβ+sinαsinβ
A(1,0), P1(cosα,sinα), A1(cosβ, sinβ),P(cos(α-β), sin(α-β))
2、两角差的余弦公式
有了公式C(α-β)以后,只要知道cosα,cosβ, sinα,sinβ的值,就可以求cos(α - β)的值了.
同名积,符号反
差角的余弦公式
简记为:C(α-β)
2).对于α,β,只要知道其正弦或余弦,就可求出cos(α-β)
1).公式的结构特征:
左边是复角α-β的余弦,右边是单角α、β 的余弦积与正弦积的和.
判断正误.(请在括号中打“√”或“×”)
(1)对于任意α, β∈R, cos(α-β)=cos αcos β+sin αsin β都成立. ( )
(2)对于任意α, β∈R, cos(α-β)=cos α-cos β都不成立. ( )
(3)cos 300cos 1200+sin 300sin 1200=0. ( )
√
×
√
解: (1)该结论为两角差的余弦公式.
解: (2)当α= -450, β=450时,
cos(α-β)=cos α-cos β.
解: (3)cos 300cos 1200+sin 300sin1200
=cos(1200-300)=cos 900=0.
差角的余弦公式的简单应用(证明、化简、求值)
例1
(1)cos 15°的值是
√
完成本题后,你会求sin75o 的值吗?
两角差的余弦公式常见题型及解法
(1)两特殊角之差的余弦值,利用两角差的余弦公式直接展开求解.
(2)含有常数的式子,先将系数转化为特殊角的三角函数值,再利用两角差的余弦公式求解.
(3)求非特殊角的三角函数值,把非特殊角转化为两个特殊角的差,然后利用两角差的余弦公式求解.
反思感悟
跟踪训练1
求下列各式的值:
(1)cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
原式=cos[θ+21°-(θ-24°)]
(2)-sin 167°·sin 223°+sin 257°·sin 313°;
原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)·sin(360°-47°)
=sin 13°sin 43°+sin 77°sin 47°
=sin 13°sin 43°+cos 13°cos 43°
给值求值
例2
√
给值求值的解题策略
(1)已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.常见角的变换有:
反思感悟
跟踪训练2
所以0<α+β<π,
所以cos β=cos[(α+β)-α]
例3
给值求角
∵β=α-(α-β),
∴cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)
反思感悟
已知三角函数值求角的解题步骤
(1)界定角的范围,根据条件确定所求角的范围.
(2)求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.
(3)结合三角函数值及角的范围求角.
提醒:由三角函数值求角时,易忽视角的范围,而得到错误答案.
跟踪训练3
∴cos(α-β)=cos αcos β+sin αsin β
∵α,β均为锐角,
课堂
小结
1.知识清单:
(1)两角差的余弦公式的推导.
(2)给角求值、给值求值、给值求角.
2.方法归纳:构造法.
3.常见误区:求角时忽视角的范围.
前面我们学习了诱导公式,利用它们对三角函数式进行恒等变形,可以达到化简、求值或证明的目的.这种利用公式对三角函数式进行的恒等变形就是三角恒等变换.
观察诱导公式,可以发现它们都是特殊角与任意角α的和 (或差)的三角函数与这个任意角α的三角函数的恒等关系.如
如果把特殊角换为任意角β,那么任意角α与β的和 (或差)的三角函数与α,β的三角函数会有什么关系呢?
cos(π-α)= - cosα
如怎样求cos(β-α)呢?下面来研究这个问题.
两角差的余弦公式
学习目标
1.熟悉两角差的余弦公式的推导过程.
2.掌握两角差的余弦公式的应用.
在坐标平面内的任意两点P1(x1, y1), P2(x2, y2),如图,过P1, P2分别作x轴,y轴的垂线交于点Q,则Q的坐标为(x2,y1),则
由勾股定理,可得:
所以平面内P1(x1, y1), P2(x2, y2)两点间距离:
x
y
O
P1(x1, y1)
P2(x2, y2)
Q(x2, y1)
∟
∟
1、平面内两点间距离公式
α终边
β终边
α-β终边
如图,设单位圆于x轴的正半轴相交于点A(1,0),
以x轴非负半轴为始边作角α,β ,α-β ,它们
的终边分别与单位圆相交于点P1(cosα,sinα), A1(cosβ, sinβ),P(cos(α-β), sin(α-β)).
下面我们来探究cos(α-β)角α,β的正弦、余弦之间的关系.
不妨令α≠2kπ+β,k∈Z,
如果已知任意角α,β的正弦、余弦,能由此推出α-β的正弦、余弦吗?
探究
α终边
β终边
α-β终边
连接A1P1,AP.若把扇形OAP绕着点O旋转β角,则点A,P分别与点A1,P1重合.根据圆的旋转对称性可知:
AP 与A1P1重合,从而AP = A1P1 ,所以AP = A1P1.
根据两点间的距离公式,得:
当α=2kπ+β, k∈Z时,
容易证明上式仍然成立.
[cos(α-β)-1]2+[sin(α-β)]2
=(cosα -cosβ)2 +(sinα -sinβ)2
化简得:
cos(α-β)=cosαcosβ+sinαsinβ
A(1,0), P1(cosα,sinα), A1(cosβ, sinβ),P(cos(α-β), sin(α-β))
2、两角差的余弦公式
有了公式C(α-β)以后,只要知道cosα,cosβ, sinα,sinβ的值,就可以求cos(α - β)的值了.
同名积,符号反
差角的余弦公式
简记为:C(α-β)
2).对于α,β,只要知道其正弦或余弦,就可求出cos(α-β)
1).公式的结构特征:
左边是复角α-β的余弦,右边是单角α、β 的余弦积与正弦积的和.
判断正误.(请在括号中打“√”或“×”)
(1)对于任意α, β∈R, cos(α-β)=cos αcos β+sin αsin β都成立. ( )
(2)对于任意α, β∈R, cos(α-β)=cos α-cos β都不成立. ( )
(3)cos 300cos 1200+sin 300sin 1200=0. ( )
√
×
√
解: (1)该结论为两角差的余弦公式.
解: (2)当α= -450, β=450时,
cos(α-β)=cos α-cos β.
解: (3)cos 300cos 1200+sin 300sin1200
=cos(1200-300)=cos 900=0.
差角的余弦公式的简单应用(证明、化简、求值)
例1
(1)cos 15°的值是
√
完成本题后,你会求sin75o 的值吗?
两角差的余弦公式常见题型及解法
(1)两特殊角之差的余弦值,利用两角差的余弦公式直接展开求解.
(2)含有常数的式子,先将系数转化为特殊角的三角函数值,再利用两角差的余弦公式求解.
(3)求非特殊角的三角函数值,把非特殊角转化为两个特殊角的差,然后利用两角差的余弦公式求解.
反思感悟
跟踪训练1
求下列各式的值:
(1)cos(θ+21°)cos(θ-24°)+sin(θ+21°)sin(θ-24°);
原式=cos[θ+21°-(θ-24°)]
(2)-sin 167°·sin 223°+sin 257°·sin 313°;
原式=-sin(180°-13°)sin(180°+43°)+sin(180°+77°)·sin(360°-47°)
=sin 13°sin 43°+sin 77°sin 47°
=sin 13°sin 43°+cos 13°cos 43°
给值求值
例2
√
给值求值的解题策略
(1)已知某些角的三角函数值,求另外一些角的三角函数值,要注意观察已知角与所求表达式中角的关系,即拆角与凑角.
(2)由于和、差角与单角是相对的,因此解题过程中根据需要灵活地进行拆角或凑角的变换.常见角的变换有:
反思感悟
跟踪训练2
所以0<α+β<π,
所以cos β=cos[(α+β)-α]
例3
给值求角
∵β=α-(α-β),
∴cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)
反思感悟
已知三角函数值求角的解题步骤
(1)界定角的范围,根据条件确定所求角的范围.
(2)求所求角的某种三角函数值.为防止增解最好选取在范围内单调的三角函数.
(3)结合三角函数值及角的范围求角.
提醒:由三角函数值求角时,易忽视角的范围,而得到错误答案.
跟踪训练3
∴cos(α-β)=cos αcos β+sin αsin β
∵α,β均为锐角,
课堂
小结
1.知识清单:
(1)两角差的余弦公式的推导.
(2)给角求值、给值求值、给值求角.
2.方法归纳:构造法.
3.常见误区:求角时忽视角的范围.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
