2022-2023学年高一上学期数学人教A版(2019)必修第一册5.5.1 第4课时 二倍角的正弦、余弦、正切公式 课件-(共25张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册5.5.1 第4课时 二倍角的正弦、余弦、正切公式 课件-(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 13:24:09 | ||
图片预览








文档简介
(共25张PPT)
同学们,唐代诗人王维曾写出“独在异乡为异客,每逢佳节倍思亲”,一个“倍”字道出了思念亲人的急迫心情,这里的“倍”何止二倍、三倍,更是百倍、千倍,就像大家期盼放假一样的心情。
同学们,让我们加倍努力,期待我们的成绩加倍提高,说不定,放假时,你们的父母会对你们有加倍的奖励哦。
今天,就让我们共同探究三角函数中的“二倍”关系.
二倍角的正弦、余弦、正切公式
学习目标
1.会用两角和(差)的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的三角恒等变换并能灵活地将公式变形运用.
以公式C(α-β) 为基础,我们已经得到了六个和(差)角公式,下面我们以和角公式为基础来推导被叫公式。
请同学们写出两角和的正弦、余弦、正切公式.
sin(α+β)=sin αcos β+cos αsin β;
cos(α+β)=cos αcos β-sin αsin β;
α=β
得
化简可
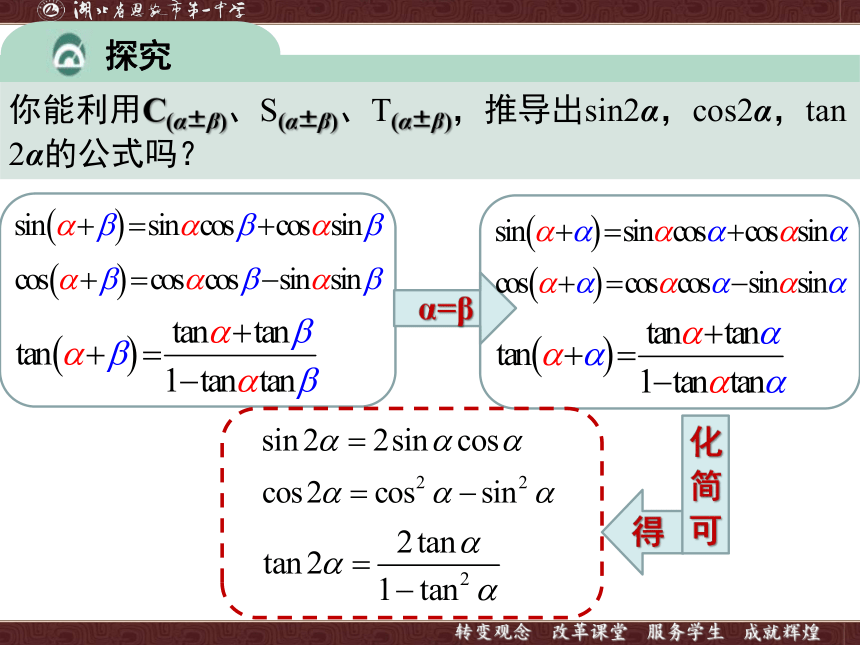
你能利用C(α±β)、S(α±β)、T(α±β),推导出sin2α,cos2α,tan2α的公式吗?
探究
以上这些公式都叫做倍角公式,倍角公式给出了α的三角函数与2α的三角函数之间的关系.
注:这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去.
二倍角的正弦、余弦、正切公式:
降次
公式
升次
公式
二倍角的正弦、余弦、正切公式:
二倍角的正弦、余弦、正切公式:
【解析】由 ,得 ,
又 ,所以 .
于是
“倍”是描述两个数量之间的关系,2α是α的二倍,4α是2α的二倍,α是 的二倍,
是 的二倍角.
应用:给值求值
例5
例6
例6
解决给值求值问题的方法
(1)给值求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向:
①有方向地将已知式或未知式化简,使关系明朗化;
②寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
反思感悟
跟踪训练2
∵θ∈(0,π),∴sin θ>0,cos θ<0,
求下列各式的值:
(3)cos 20°·cos 40°·cos 80°.
例1
应用:给角求值
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
反思感悟
求下列各式的值:
跟踪训练1
例3
倍角公式的综合运用
(2)若f(B)-m>2恒成立,求实数m的取值范围.
由题意知f(B)-m>2恒成立,
因为0所以2+m<-2,所以m<-4,
故实数m的取值范围是(-∞,-4).
(2)若f(B)-m>2恒成立,求实数m的取值范围.
反思感悟
要结合之前所学的所有的公式,对它们灵活运用,融会贯通,在解决具体问题时,要注意题目中的隐含条件,要会对三角函数值的符号进行判断.尤其是在三角形中,其最多只有一个直角或钝角,正弦值均为正,余弦和正切值并不一定为正.
跟踪训练3
√
∴sin α>0,cos α<0,∴cos α-sin α<0,
∴cos 2α=cos2α-sin2α=(cos α+sin α)(cos α-sin α)
课堂
小结
1.知识清单:
(1)二倍角公式的推导.
(2)利用二倍角公式的正用、逆用进行化简、求值和证明.
2.方法归纳:转化法.
3.常见误区:化简求值开根号时,忽视角的范围、实际问题中隐含的条件.
同学们,唐代诗人王维曾写出“独在异乡为异客,每逢佳节倍思亲”,一个“倍”字道出了思念亲人的急迫心情,这里的“倍”何止二倍、三倍,更是百倍、千倍,就像大家期盼放假一样的心情。
同学们,让我们加倍努力,期待我们的成绩加倍提高,说不定,放假时,你们的父母会对你们有加倍的奖励哦。
今天,就让我们共同探究三角函数中的“二倍”关系.
二倍角的正弦、余弦、正切公式
学习目标
1.会用两角和(差)的正弦、余弦、正切公式推导出二倍角的正弦、余弦、正切公式.
2.能熟练运用二倍角的公式进行简单的三角恒等变换并能灵活地将公式变形运用.
以公式C(α-β) 为基础,我们已经得到了六个和(差)角公式,下面我们以和角公式为基础来推导被叫公式。
请同学们写出两角和的正弦、余弦、正切公式.
sin(α+β)=sin αcos β+cos αsin β;
cos(α+β)=cos αcos β-sin αsin β;
α=β
得
化简可
你能利用C(α±β)、S(α±β)、T(α±β),推导出sin2α,cos2α,tan2α的公式吗?
探究
以上这些公式都叫做倍角公式,倍角公式给出了α的三角函数与2α的三角函数之间的关系.
注:这里的“倍角”专指“二倍角”,遇到“三倍角”等名词时,“三”字等不可省去.
二倍角的正弦、余弦、正切公式:
降次
公式
升次
公式
二倍角的正弦、余弦、正切公式:
二倍角的正弦、余弦、正切公式:
【解析】由 ,得 ,
又 ,所以 .
于是
“倍”是描述两个数量之间的关系,2α是α的二倍,4α是2α的二倍,α是 的二倍,
是 的二倍角.
应用:给值求值
例5
例6
例6
解决给值求值问题的方法
(1)给值求值问题,注意寻找已知式与未知式之间的联系,有两个观察方向:
①有方向地将已知式或未知式化简,使关系明朗化;
②寻找角之间的关系,看是否适合相关公式的使用,注意常见角的变换和角之间的二倍关系.
反思感悟
跟踪训练2
∵θ∈(0,π),∴sin θ>0,cos θ<0,
求下列各式的值:
(3)cos 20°·cos 40°·cos 80°.
例1
应用:给角求值
对于给角求值问题,一般有两类
(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式子进行转化,一般可以化为特殊角.
(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.
反思感悟
求下列各式的值:
跟踪训练1
例3
倍角公式的综合运用
(2)若f(B)-m>2恒成立,求实数m的取值范围.
由题意知f(B)-m>2恒成立,
因为0
故实数m的取值范围是(-∞,-4).
(2)若f(B)-m>2恒成立,求实数m的取值范围.
反思感悟
要结合之前所学的所有的公式,对它们灵活运用,融会贯通,在解决具体问题时,要注意题目中的隐含条件,要会对三角函数值的符号进行判断.尤其是在三角形中,其最多只有一个直角或钝角,正弦值均为正,余弦和正切值并不一定为正.
跟踪训练3
√
∴sin α>0,cos α<0,∴cos α-sin α<0,
∴cos 2α=cos2α-sin2α=(cos α+sin α)(cos α-sin α)
课堂
小结
1.知识清单:
(1)二倍角公式的推导.
(2)利用二倍角公式的正用、逆用进行化简、求值和证明.
2.方法归纳:转化法.
3.常见误区:化简求值开根号时,忽视角的范围、实际问题中隐含的条件.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
