5.6.2函数y=Asin(wx-φ)的图象 课件(共两课时)-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共43张PPT)
文档属性
| 名称 | 5.6.2函数y=Asin(wx-φ)的图象 课件(共两课时)-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 12:24:04 | ||
图片预览



文档简介
(共43张PPT)
5.6函数y=Asin( x+ )(第一课时)
2
o
y
x
y=sinx
3
2
2
1
-1
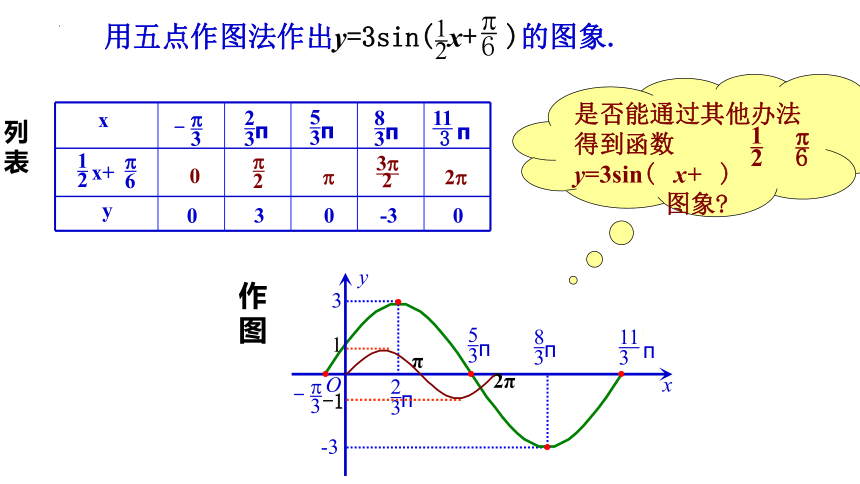
⒈正弦函数的图象
⒉五点法作图:
复习引入
在一个正弦函数周期内,选择五个特殊点先连线作出函数在一个周期内的图象,然后再根据周期性,作出函数的全部图象。
⒊函数图象的变换:
①平移变换:
②翻转变换:
③翻折变换:
④伸缩变换:
y=f (x+m) ; y=f (x)+n
y=-f (x); y=f (-x)
y=|f (x)|; y=f (|x|)
y=A f(x); y=f ( x)
1113
π
53
π
-
3
0
2
3
2
2
0
0
3
0
-3
列表
y
x
x
8 3
π
y
O
53
π
2 3
π
11 13
π
3
-3
作图
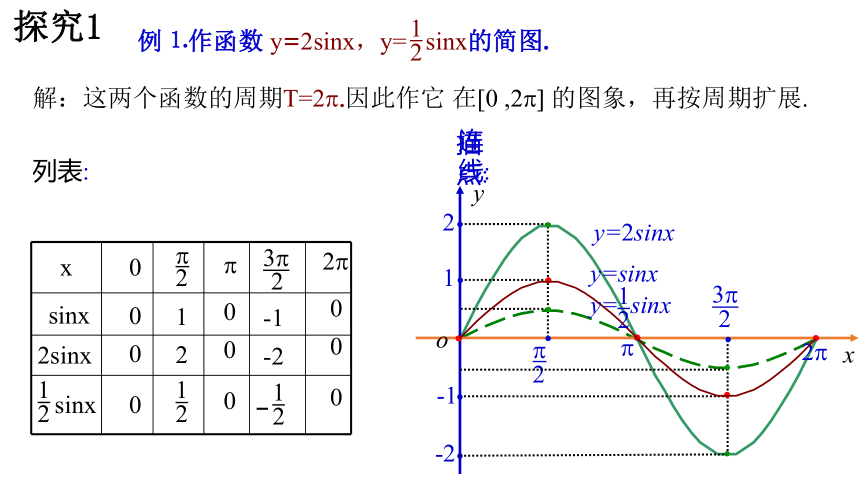
用五点作图法作出y=3sin( x+ )的图象.
6
12
-
3
83
π
2 3
π
π
2π
1
-1
x+
6
12
是否能通过其他办法得到函数y=3sin( x+ )
图象
12
6
解:这两个函数的周期T=2 .因此作它 在[0 ,2 ] 的图象,再按周期扩展.
例⒈作函数 y=2sinx,y= sinx的简图.
12
列表:
x
0
0
sinx
12
12
0
0
12
2
3
2
2
sinx
0
1
0
-1
2sinx
0
0
2
0
-2
0
探究1
-1
3
2
2
o
y
2
x
描点:
1
2
-2
连线:
y=sinx
y=2sinx
y= sinx
12
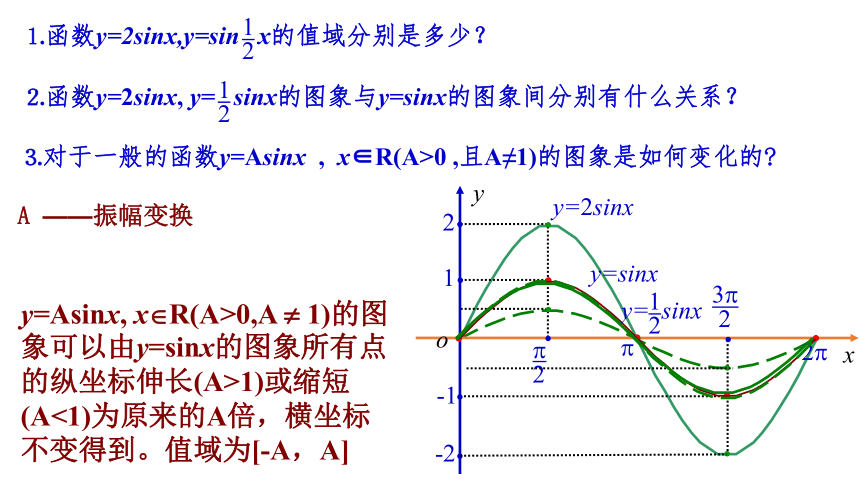
⒈函数y=2sinx,y=sin x的值域分别是多少?
12
⒉函数y=2sinx, y= sinx的图象与y=sinx的图象间分别有什么关系?
12
⒊对于一般的函数y=Asinx , x∈R(A>0 ,且A≠1)的图象是如何变化的
-1
3
2
2
o
y
2
x
1
2
-2
y=sinx
y=2sinx
y= sinx
12
A ——振幅变换
y=Asinx, x R(A>0,A 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
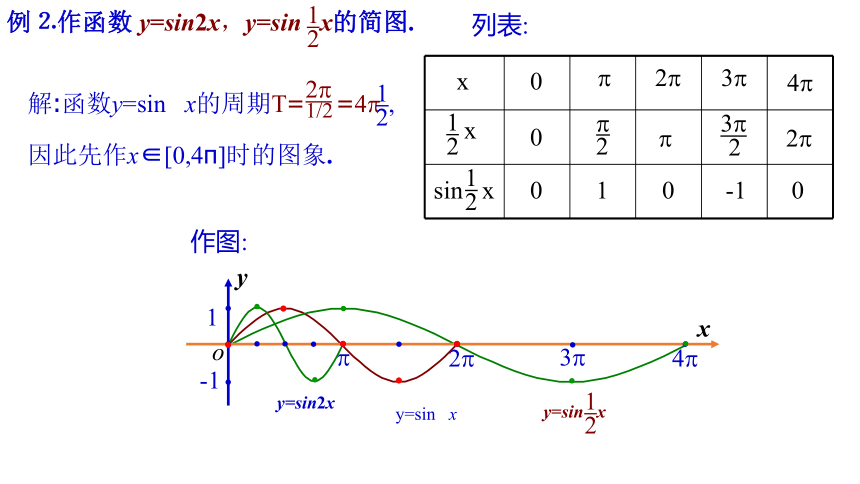
例⒉作函数 y=sin2x,y=sin x的简图.
12
解:函数y=sin2x的周期T= = ,因此先作x∈[0,π]时的图象.
2
2
列表:
x
0
4
3
4
2x
0
2
3
2
2
2
sin2x
0
1
0
-1
0
探究2
1
2
o
y
x
作图:
-1
列表:
解:函数y=sin x的周期T= =4 ,
因此先作x∈[0,4π]时的图象.
2
1/2
12
例⒉作函数 y=sin2x,y=sin x的简图.
12
x
0
4
3
2
2
3
2
2
1
0
-1
0
x
12
sin x
12
0
0
1
2
3
4
o
y
x
作图:
-1
y=sin2x
y=sin x
y=sin x
12
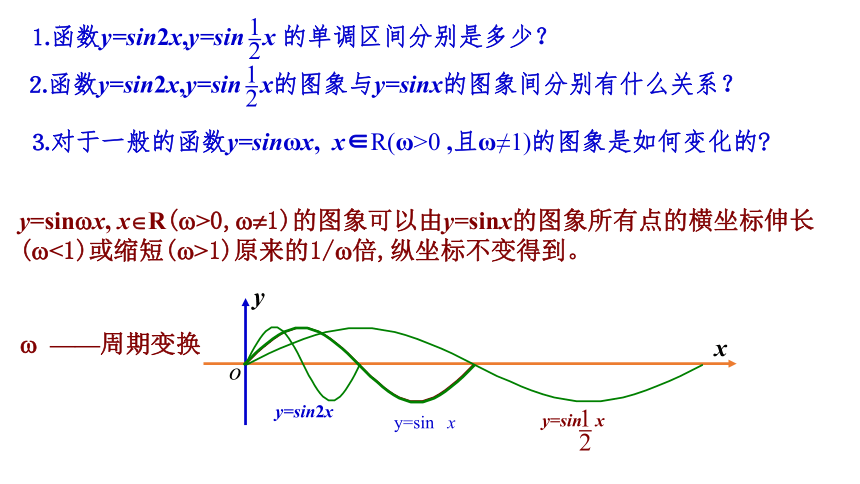
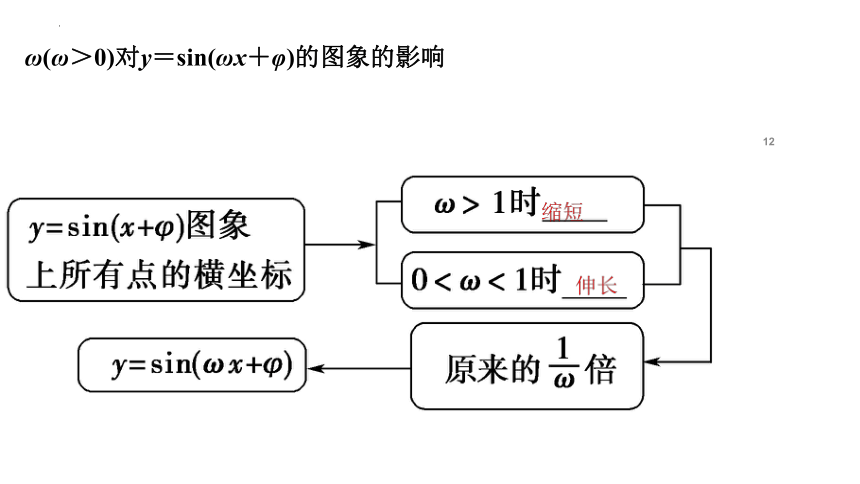
⒊对于一般的函数y=sinωx, x∈R(ω>0 ,且ω≠1)的图象是如何变化的
⒈函数y=sin2x,y=sin x 的单调区间分别是多少?
12
⒉函数y=sin2x,y=sin x的图象与y=sinx的图象间分别有什么关系?
12
o
y
x
y=sin x, x R( >0, 1)的图象可以由y=sinx的图象所有点的横坐标伸长( <1)或缩短( >1)原来的1/ 倍,纵坐标不变得到。
——周期变换
y=sin2x
y=sin x
y=sin x
12
振 变
幅 换
周 变
期 换
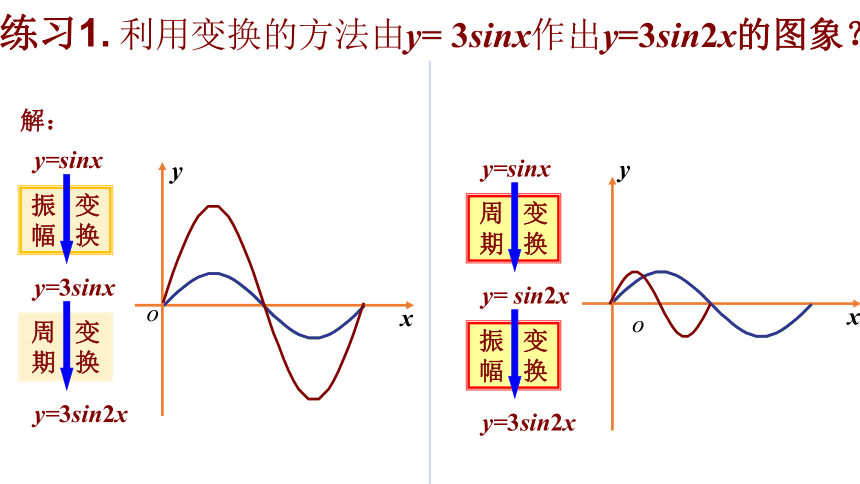
利用变换的方法由y= 3sinx作出y=3sin2x的图象?
解:
y=3sinx
y=sinx
y=3sin2x
o
y
x
练习1.
周 变
期 换
y= sin2x
y=sinx
y=3sin2x
振 变
幅 换
o
y
x
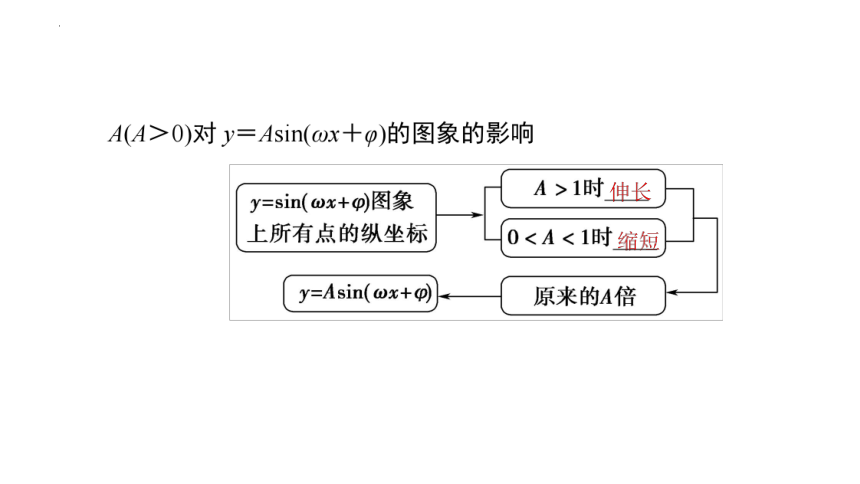
ω(ω>0)对y=sin(ωx+φ)的图象的影响
12
在包含振幅变换和周期变换的复合变换中,无论先经过振幅变换还是先经过周期变换所得的结果一致。
振幅变换
周期变换
y=Asinx
周期变换
y= sinωx
y=sinx
y=Asinωx
振幅变换
总结
x
x+
sin(x + )
0 1 0 -1 0
0 2
_
y=sinx
x
-1
1
o
y
-
y=sin(x+ )
兀
3
例⒊作函数 y=sin(x+ ),
y=sin(x- )的简图.
3
4
探究3
x
-1
1
o
y
-
x
0 1 0 -1 0
0 2
y=sinx
y=sin(x+ )
兀
3
例⒊作函数 y=sin(x+ ),
y=sin(x- )的简图.
3
4
探究3
x
9
4
5
4
4
2
3
5
3
-
3
例⒊作函数 y=sin(x+ ),y=sin(x- )的简图.
3
4
解:由平移变换: y=f (x+m)表示将f (x)的图象向左平移m个单位。
o
y
1
2
-1
探究3
∴函数y=sin(x+ )的图象可以看作把正弦曲线上所有点向左平移 个单位而得到。
3
3
∴函数y=sin(x- )的图象可以看作把正弦曲线上所有点向右平移 个单位而得到。
4
4
——相位变换
y=sin(x+ ), x R( 0)的图象可以由y=sinx的图象上所有点向左( >0)或向右( <0)平移| |个单位,纵坐标不变得到。
总结
x
9
4
5
4
4
2
3
5
3
-
3
o
y
1
2
-1
相 变
位 换
振 变
幅 换
解:
y=sinx
y
o
x
y=3sin(x+ )
3
y= sin(x+ )
3
利用变换的方法作出y=3sin(x+ )的图象?
3
练习
振 变
幅 换
相 变
位 换
y=sinx
y=3sin(x+ )
3
y= 3sinx
y
o
x
振幅变换
相位变换
y=Asinx
相位变换
y=sin(x+ )
y=sinx
y=Asin(x+ )
振幅变换
在包含振幅变换和相位变换的复合变换中,无论先经过振幅变换还是先经过相位变换所得的结果一致。
总结
利用变换的方法作出y=sin(2x+ )的图象?
3
练习2.
解:
y=sinx
y
o
x
y=sin(2x+ )
3
相 变
位 换
y= sin(x+ )
3
周 变
期 换
y=sinx
y=sin(2x+ )
3
周 变
期 换
y= sin2x
相 变
位 换
y
o
x
此时平移的是多少个单位
周期变换
相位变换
y=sinωx
相位变换
y=sin(x+ )
y=sinx
y=sin(ωx+ )
周期变换
在包含周期变换和相位变换的复合变换中,无论先经过周期变换还是先经过相位变换所得的结果一致。
在先经过周期变换,再进行相位变换的时候,实际平移的是 / 个单位。
总结
无论周期变换还是相位变换都是直接作用在x上的!!!
振幅变换
解:
y=sinx
y
o
x
y=sin( x+ )
6
12
相 变
位 换
y= sin(x+ )
6
周 变
期 换
y=3sin( x+ )
6
12
利用图象变换的方法作出y=3sin( x+ )的图象.
6
12
练习3.
振幅变换
y=sinx
y
o
x
y=sin( x+ )
6
12
周 变
期 换
相 变
位 换
y=3sin( x+ )
6
12
y=sin x
1
2
你能总结一下从正弦函数图象出发 , 通过图象变换得到 y=Asin(ωx+φ) ( A >0 ,ω >0 ) 图象的过程与方法吗
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:(按 φ , ω ,A顺序变换)
平移| |个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0y=Asin( x+ )
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
方法2:(按按 ω , φ ,A顺序变换)
向左 >0 (向右 <0)
平移| |/ 个单位
分析(1)依据左加右减;上加下减的规则写出解析式.
(2)法一:y=sin x→纵坐标伸缩→横坐标伸缩和平移→向上平移.
法二:左右平移→横坐标伸缩→纵坐标伸缩→上下平移.
分析:由最大(小)值求A和B,由周期求ω,由特殊点坐标解方程求φ.
提示:与正弦曲线、余弦曲线一样,函数y=Asin(ωx+φ)和y=Acos(ωx+φ)图象的对称中心即函数图象与x轴的交点.
y=Asinx, x R(A>0,A 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
A ——振幅变换
y=sin x, x R( >0, 1)的图象可以由y=sinx的图象所有点的横坐标伸长( <1)或缩短( >1)原来的1/ 倍,纵坐标不变得到。
——周期变换
——相位变换
y=sin(x+ ), x R( 0)的图象可以由y=sinx的图象上所有点向左( >0)或向右( <0)平移| |个单位,纵坐标不变得到。
小结
周期变换
y=sinωx
相位变换
y=sin(x+ )
y=sinx
y=sin(ωx+ )
周期变换
振幅变换
y=Asin(ωx+ )
相位变换
在先经过周期变换,再进行相位变换的时候,实际平移的是 / 个单位。
无论周期变换还是相位变换都是直接作用在x上的!!!
布置作业
课后练习1、2
5.6函数y=Asin( x+ )(第一课时)
2
o
y
x
y=sinx
3
2
2
1
-1
⒈正弦函数的图象
⒉五点法作图:
复习引入
在一个正弦函数周期内,选择五个特殊点先连线作出函数在一个周期内的图象,然后再根据周期性,作出函数的全部图象。
⒊函数图象的变换:
①平移变换:
②翻转变换:
③翻折变换:
④伸缩变换:
y=f (x+m) ; y=f (x)+n
y=-f (x); y=f (-x)
y=|f (x)|; y=f (|x|)
y=A f(x); y=f ( x)
1113
π
53
π
-
3
0
2
3
2
2
0
0
3
0
-3
列表
y
x
x
8 3
π
y
O
53
π
2 3
π
11 13
π
3
-3
作图
用五点作图法作出y=3sin( x+ )的图象.
6
12
-
3
83
π
2 3
π
π
2π
1
-1
x+
6
12
是否能通过其他办法得到函数y=3sin( x+ )
图象
12
6
解:这两个函数的周期T=2 .因此作它 在[0 ,2 ] 的图象,再按周期扩展.
例⒈作函数 y=2sinx,y= sinx的简图.
12
列表:
x
0
0
sinx
12
12
0
0
12
2
3
2
2
sinx
0
1
0
-1
2sinx
0
0
2
0
-2
0
探究1
-1
3
2
2
o
y
2
x
描点:
1
2
-2
连线:
y=sinx
y=2sinx
y= sinx
12
⒈函数y=2sinx,y=sin x的值域分别是多少?
12
⒉函数y=2sinx, y= sinx的图象与y=sinx的图象间分别有什么关系?
12
⒊对于一般的函数y=Asinx , x∈R(A>0 ,且A≠1)的图象是如何变化的
-1
3
2
2
o
y
2
x
1
2
-2
y=sinx
y=2sinx
y= sinx
12
A ——振幅变换
y=Asinx, x R(A>0,A 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
例⒉作函数 y=sin2x,y=sin x的简图.
12
解:函数y=sin2x的周期T= = ,因此先作x∈[0,π]时的图象.
2
2
列表:
x
0
4
3
4
2x
0
2
3
2
2
2
sin2x
0
1
0
-1
0
探究2
1
2
o
y
x
作图:
-1
列表:
解:函数y=sin x的周期T= =4 ,
因此先作x∈[0,4π]时的图象.
2
1/2
12
例⒉作函数 y=sin2x,y=sin x的简图.
12
x
0
4
3
2
2
3
2
2
1
0
-1
0
x
12
sin x
12
0
0
1
2
3
4
o
y
x
作图:
-1
y=sin2x
y=sin x
y=sin x
12
⒊对于一般的函数y=sinωx, x∈R(ω>0 ,且ω≠1)的图象是如何变化的
⒈函数y=sin2x,y=sin x 的单调区间分别是多少?
12
⒉函数y=sin2x,y=sin x的图象与y=sinx的图象间分别有什么关系?
12
o
y
x
y=sin x, x R( >0, 1)的图象可以由y=sinx的图象所有点的横坐标伸长( <1)或缩短( >1)原来的1/ 倍,纵坐标不变得到。
——周期变换
y=sin2x
y=sin x
y=sin x
12
振 变
幅 换
周 变
期 换
利用变换的方法由y= 3sinx作出y=3sin2x的图象?
解:
y=3sinx
y=sinx
y=3sin2x
o
y
x
练习1.
周 变
期 换
y= sin2x
y=sinx
y=3sin2x
振 变
幅 换
o
y
x
ω(ω>0)对y=sin(ωx+φ)的图象的影响
12
在包含振幅变换和周期变换的复合变换中,无论先经过振幅变换还是先经过周期变换所得的结果一致。
振幅变换
周期变换
y=Asinx
周期变换
y= sinωx
y=sinx
y=Asinωx
振幅变换
总结
x
x+
sin(x + )
0 1 0 -1 0
0 2
_
y=sinx
x
-1
1
o
y
-
y=sin(x+ )
兀
3
例⒊作函数 y=sin(x+ ),
y=sin(x- )的简图.
3
4
探究3
x
-1
1
o
y
-
x
0 1 0 -1 0
0 2
y=sinx
y=sin(x+ )
兀
3
例⒊作函数 y=sin(x+ ),
y=sin(x- )的简图.
3
4
探究3
x
9
4
5
4
4
2
3
5
3
-
3
例⒊作函数 y=sin(x+ ),y=sin(x- )的简图.
3
4
解:由平移变换: y=f (x+m)表示将f (x)的图象向左平移m个单位。
o
y
1
2
-1
探究3
∴函数y=sin(x+ )的图象可以看作把正弦曲线上所有点向左平移 个单位而得到。
3
3
∴函数y=sin(x- )的图象可以看作把正弦曲线上所有点向右平移 个单位而得到。
4
4
——相位变换
y=sin(x+ ), x R( 0)的图象可以由y=sinx的图象上所有点向左( >0)或向右( <0)平移| |个单位,纵坐标不变得到。
总结
x
9
4
5
4
4
2
3
5
3
-
3
o
y
1
2
-1
相 变
位 换
振 变
幅 换
解:
y=sinx
y
o
x
y=3sin(x+ )
3
y= sin(x+ )
3
利用变换的方法作出y=3sin(x+ )的图象?
3
练习
振 变
幅 换
相 变
位 换
y=sinx
y=3sin(x+ )
3
y= 3sinx
y
o
x
振幅变换
相位变换
y=Asinx
相位变换
y=sin(x+ )
y=sinx
y=Asin(x+ )
振幅变换
在包含振幅变换和相位变换的复合变换中,无论先经过振幅变换还是先经过相位变换所得的结果一致。
总结
利用变换的方法作出y=sin(2x+ )的图象?
3
练习2.
解:
y=sinx
y
o
x
y=sin(2x+ )
3
相 变
位 换
y= sin(x+ )
3
周 变
期 换
y=sinx
y=sin(2x+ )
3
周 变
期 换
y= sin2x
相 变
位 换
y
o
x
此时平移的是多少个单位
周期变换
相位变换
y=sinωx
相位变换
y=sin(x+ )
y=sinx
y=sin(ωx+ )
周期变换
在包含周期变换和相位变换的复合变换中,无论先经过周期变换还是先经过相位变换所得的结果一致。
在先经过周期变换,再进行相位变换的时候,实际平移的是 / 个单位。
总结
无论周期变换还是相位变换都是直接作用在x上的!!!
振幅变换
解:
y=sinx
y
o
x
y=sin( x+ )
6
12
相 变
位 换
y= sin(x+ )
6
周 变
期 换
y=3sin( x+ )
6
12
利用图象变换的方法作出y=3sin( x+ )的图象.
6
12
练习3.
振幅变换
y=sinx
y
o
x
y=sin( x+ )
6
12
周 变
期 换
相 变
位 换
y=3sin( x+ )
6
12
y=sin x
1
2
你能总结一下从正弦函数图象出发 , 通过图象变换得到 y=Asin(ωx+φ) ( A >0 ,ω >0 ) 图象的过程与方法吗
y=sinx
y=sin(x+ )
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin( x+ )
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
向左 >0 (向右 <0)
方法1:(按 φ , ω ,A顺序变换)
平移| |个单位
纵坐标不变
横坐标不变
y=sinx
横坐标缩短 >1 (伸长0< <1)到原来的1/ 倍
y=sin x
纵坐标伸长A>1 (缩短0
y=sinx
y=Asin( x+ )
总结:
纵坐标不变
横坐标不变
方法2:(按按 ω , φ ,A顺序变换)
向左 >0 (向右 <0)
平移| |/ 个单位
分析(1)依据左加右减;上加下减的规则写出解析式.
(2)法一:y=sin x→纵坐标伸缩→横坐标伸缩和平移→向上平移.
法二:左右平移→横坐标伸缩→纵坐标伸缩→上下平移.
分析:由最大(小)值求A和B,由周期求ω,由特殊点坐标解方程求φ.
提示:与正弦曲线、余弦曲线一样,函数y=Asin(ωx+φ)和y=Acos(ωx+φ)图象的对称中心即函数图象与x轴的交点.
y=Asinx, x R(A>0,A 1)的图象可以由y=sinx的图象所有点的纵坐标伸长(A>1)或缩短(A<1)为原来的A倍,横坐标不变得到。值域为[-A,A]
A ——振幅变换
y=sin x, x R( >0, 1)的图象可以由y=sinx的图象所有点的横坐标伸长( <1)或缩短( >1)原来的1/ 倍,纵坐标不变得到。
——周期变换
——相位变换
y=sin(x+ ), x R( 0)的图象可以由y=sinx的图象上所有点向左( >0)或向右( <0)平移| |个单位,纵坐标不变得到。
小结
周期变换
y=sinωx
相位变换
y=sin(x+ )
y=sinx
y=sin(ωx+ )
周期变换
振幅变换
y=Asin(ωx+ )
相位变换
在先经过周期变换,再进行相位变换的时候,实际平移的是 / 个单位。
无论周期变换还是相位变换都是直接作用在x上的!!!
布置作业
课后练习1、2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
