人教A版数学选修2-1 1.2.2 充要条件 课件(15张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 1.2.2 充要条件 课件(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 154.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:08:12 | ||
图片预览






文档简介
(共15张PPT)
1.2.2 充要条件
充分条件,必要条件的定义:
若 ,则p是q成立的____条件
q是p成立的____条件
充分
必要
复习回顾
问题分析
问题:已知p:菱形是正方形,
q:邻边相等的矩形是正方形,
那么p是q的什么条件?
q又是p的什么条件
p q, 所以p是q的充分条件,q是p的必要条件.
q p, 所以q是p的充分条件,p是q的必要条件.
定义:如果既有 ,又有 ,就说,p是q的充分必要条件,简称充要条件,记作 。
显然,如果p是q的充要条件,那么q也是p的充要条件。
例题讲解:
例1.下列各题中,哪些p是q的充要条件?
(1) p:c=a=0,q:函数f(x)=ax2+bx+c是奇函数;
(2) p:x > 1,y >2,q: xy> 2;
(3) p: a -1> b -1,q: a + c > b + c;
(4) p:x > 2025, ,q: x >20 10;
(5) p: a +2> b+2 ,q: a2 > b2.
命题(1)和(3)中,p q,故p 是q的充要条件;
命题(2)中,p q ,但q p,故p 不是q的充要条件;
命题(4)中,p q ,但q p,故p 不是q的充要条件;
命题(5)中,p q ,且q p,故p 不是q的充要条件;
解:
知识归纳
几种逻辑推理关系:
(1)若p q ,q p, 则p是q的 .
p q
充分不必要条件
(2)若p q ,q p, 则p是q的 .
必要不充分条件
(3)若p q ,q p, 则p是q的 .
充要条件
(4)若p q ,q p, 则p是q的 .
既不充分也不必要条件
知识深化
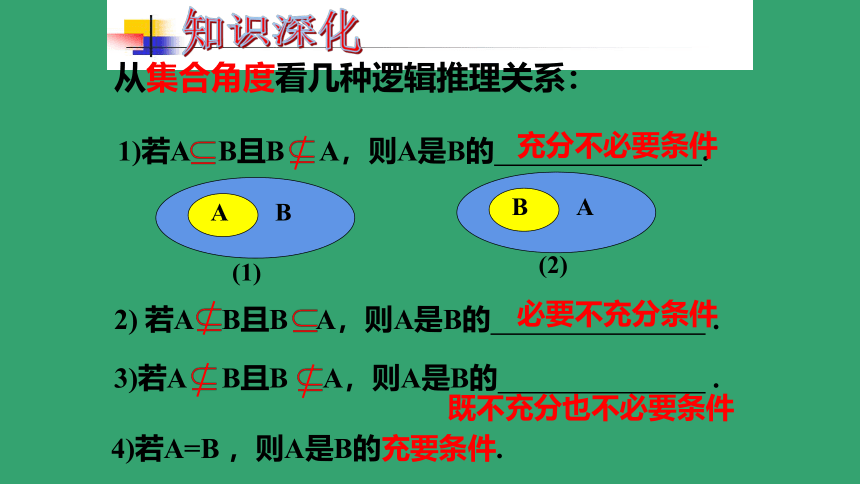
从集合角度看几种逻辑推理关系:
1)若A B且B A,则A是B的 .
充分不必要条件
必要不充分条件
既不充分也不必要条件
4)若A=B ,则A是B的充要条件.
2) 若A B且B A,则A是B的 .
3)若A B且B A,则A是B的 .
A
B
(1)
B
A
(2)
课堂练习:
必要不充分条件
充分不必要条件
充要条件
充要条件
如何从原命题和逆命题的真假性理解上述四种关系?
原命题为真,逆命题为假;
p是q的充分不必要条件,
p是q的必要不充分条件,
原命题为假,逆命题为真;
深入理解
如何从原命题和逆命题的真假性理解上述四种关系?
p是q的既不充分也不必要条件,
p是q的充要条件,
原命题、逆命题都为真;
原命题、逆命题都为假.
深入理解:
例2. 已知:a,b,c,d>0,a+b+c+d=4.
求证:
应用示例:
注意:
充要条件的证明具备“双向性”:既要证明充分性,又要证明必要性。
例3. 已知:a,b,c,d>0,a+b+c+d+abcd=5.
求证:
巩固练习
变.若A是B的必要而不充分条件,C是B的充
要条件,D是C的充分而不必要条件,
那么D是A的________
充分不必要条件
1.已知p,q都是r的必要条件,s是r的充分条件,
q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)p是q的什么条件?
充要条件
充要条件
必要不充分条件
2.已知p是q的必要而不充分条件,
那么┐p是┐q的_______________.
充分不必要条件
注:等价转换法(转化为逆否命题)
3.若┐A是┐B的充要条件,┐C是┐B的充要条件,
则A为C的( )条件.
A.充要 B.必要不充分
C.充分不必要 D.不充分不必要
A
巩固练习
3.已知p是q的充分而不必要条件,
那么┐q是┐p的_______________.
必要不充分条件
注:等价转换法(转化为逆否命题)
4.若┐A是┐B的充要条件,┐C是┐B的充要条件, ┐D是┐C的充要条件,
则A为D的( )条件.
A.充要 B.必要不充分
C.充分不必要 D.不充分不必要
A
巩固练习
小结
1.几种逻辑推理关系:
充分不必要条件、
必要不充分条件、
充要条件、
既不充分也不必要条件.
2.从集合角度看几种逻辑推理关系
3.核心素养:逻辑推理能力
1.2.2 充要条件
充分条件,必要条件的定义:
若 ,则p是q成立的____条件
q是p成立的____条件
充分
必要
复习回顾
问题分析
问题:已知p:菱形是正方形,
q:邻边相等的矩形是正方形,
那么p是q的什么条件?
q又是p的什么条件
p q, 所以p是q的充分条件,q是p的必要条件.
q p, 所以q是p的充分条件,p是q的必要条件.
定义:如果既有 ,又有 ,就说,p是q的充分必要条件,简称充要条件,记作 。
显然,如果p是q的充要条件,那么q也是p的充要条件。
例题讲解:
例1.下列各题中,哪些p是q的充要条件?
(1) p:c=a=0,q:函数f(x)=ax2+bx+c是奇函数;
(2) p:x > 1,y >2,q: xy> 2;
(3) p: a -1> b -1,q: a + c > b + c;
(4) p:x > 2025, ,q: x >20 10;
(5) p: a +2> b+2 ,q: a2 > b2.
命题(1)和(3)中,p q,故p 是q的充要条件;
命题(2)中,p q ,但q p,故p 不是q的充要条件;
命题(4)中,p q ,但q p,故p 不是q的充要条件;
命题(5)中,p q ,且q p,故p 不是q的充要条件;
解:
知识归纳
几种逻辑推理关系:
(1)若p q ,q p, 则p是q的 .
p q
充分不必要条件
(2)若p q ,q p, 则p是q的 .
必要不充分条件
(3)若p q ,q p, 则p是q的 .
充要条件
(4)若p q ,q p, 则p是q的 .
既不充分也不必要条件
知识深化
从集合角度看几种逻辑推理关系:
1)若A B且B A,则A是B的 .
充分不必要条件
必要不充分条件
既不充分也不必要条件
4)若A=B ,则A是B的充要条件.
2) 若A B且B A,则A是B的 .
3)若A B且B A,则A是B的 .
A
B
(1)
B
A
(2)
课堂练习:
必要不充分条件
充分不必要条件
充要条件
充要条件
如何从原命题和逆命题的真假性理解上述四种关系?
原命题为真,逆命题为假;
p是q的充分不必要条件,
p是q的必要不充分条件,
原命题为假,逆命题为真;
深入理解
如何从原命题和逆命题的真假性理解上述四种关系?
p是q的既不充分也不必要条件,
p是q的充要条件,
原命题、逆命题都为真;
原命题、逆命题都为假.
深入理解:
例2. 已知:a,b,c,d>0,a+b+c+d=4.
求证:
应用示例:
注意:
充要条件的证明具备“双向性”:既要证明充分性,又要证明必要性。
例3. 已知:a,b,c,d>0,a+b+c+d+abcd=5.
求证:
巩固练习
变.若A是B的必要而不充分条件,C是B的充
要条件,D是C的充分而不必要条件,
那么D是A的________
充分不必要条件
1.已知p,q都是r的必要条件,s是r的充分条件,
q是s的充分条件,则
(1)s是q的什么条件?
(2)r是q的什么条件?
(3)p是q的什么条件?
充要条件
充要条件
必要不充分条件
2.已知p是q的必要而不充分条件,
那么┐p是┐q的_______________.
充分不必要条件
注:等价转换法(转化为逆否命题)
3.若┐A是┐B的充要条件,┐C是┐B的充要条件,
则A为C的( )条件.
A.充要 B.必要不充分
C.充分不必要 D.不充分不必要
A
巩固练习
3.已知p是q的充分而不必要条件,
那么┐q是┐p的_______________.
必要不充分条件
注:等价转换法(转化为逆否命题)
4.若┐A是┐B的充要条件,┐C是┐B的充要条件, ┐D是┐C的充要条件,
则A为D的( )条件.
A.充要 B.必要不充分
C.充分不必要 D.不充分不必要
A
巩固练习
小结
1.几种逻辑推理关系:
充分不必要条件、
必要不充分条件、
充要条件、
既不充分也不必要条件.
2.从集合角度看几种逻辑推理关系
3.核心素养:逻辑推理能力
