人教A版数学选修2-1 2.3.2 双曲线简单的几何性质 课件(23张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.3.2 双曲线简单的几何性质 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:10:47 | ||
图片预览





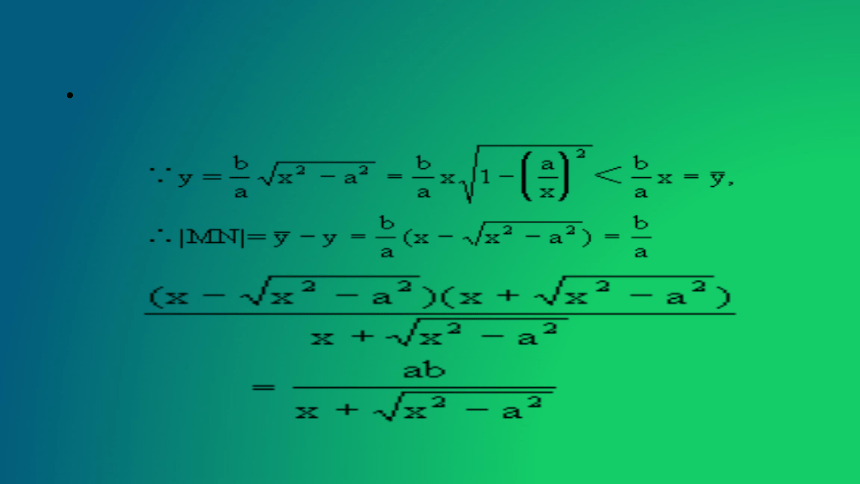

文档简介
(共23张PPT)
双曲线的简单几何性质
复习提问引入新课
1.椭圆有哪些几何性质,是如何探讨的?
请一同学回答.应为:
范围、对称性、顶点、离心率,是从标准方程探讨的.
2.双曲线的两种标准方程是什么?
再请一同学回答.应为:
中心在原点、焦点在x轴上的双曲线的标
下面我们类比椭圆的几何性质来研究它的几何性质.
在学习椭圆时,以原点为中心,2a、2b为邻边的矩形,
对于估计椭圆的形状,画出椭圆的图形有很大的作用
仍以原点为中心,2a、2b为邻边作一矩形(板书图形),那么双曲线和这个矩形有什么关系?
这个矩形对于估计和画出双曲线简图(图2-26)有什么指导意义?这些问题不要求学生回答,只引起学生类比联想.
接着再提出问题:
当a、b为已知时,这个矩形的两条对角线的方程是什么?
请一个同学回答问题
应作出 ,并画出两条对角线,进一步引导学生从图观察得出结论:双曲线的各支向外延伸是,与这两条渐进线逐渐接近
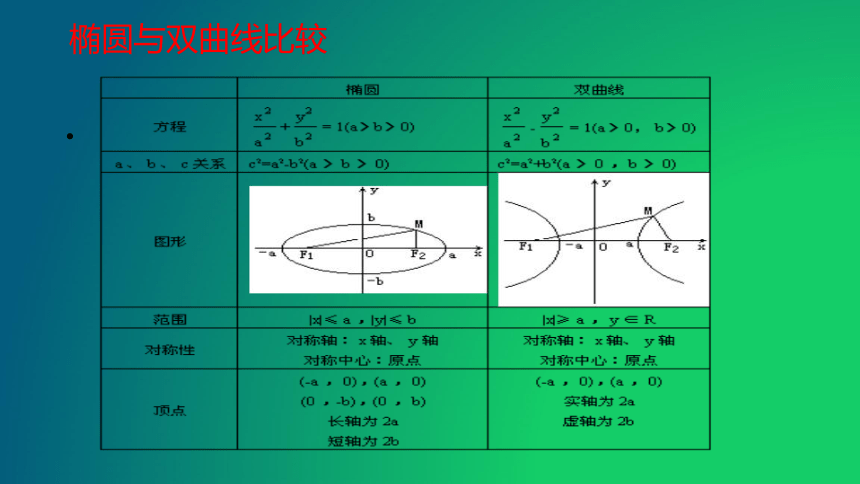
椭圆与双曲线比较
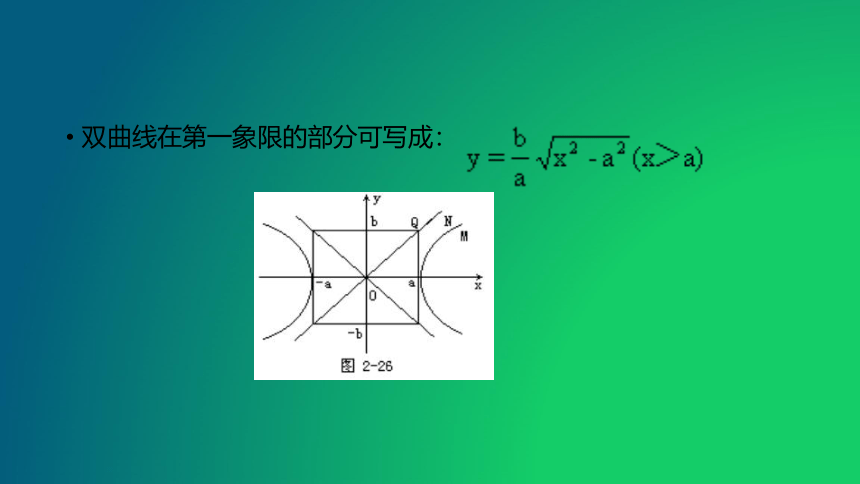
双曲线在第一象限的部分可写成:
当x逐渐增大时,|MN|逐渐减小,x无限增大,|MN|接近于零,|MQ|也接近于零,就是说,双曲线在第一象限的部分从射线ON的下方逐渐接近于射线ON.
在其他象限内也可以证明类似的情况.
现在来看看实轴在y轴上的双曲线的渐近线方程是怎样的?由于焦点在y轴上的双曲线方程是由焦点在x轴上的双曲线方程,将x、y字母对换位置,所以双曲线
离心率
双曲线的离心率越大,
它的开口就越开阔.
焦点在y轴上的双曲线的几何性质可以类似得出,
双曲线的几何性质与坐标系的选择无关,
即不随坐标系的改变而改变.
1.双曲线的焦距与实轴的比e=c/a叫做双曲线的离心率,且e>1
例题1
求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
由此可知,实半轴长a=4,虚半轴长b=3.
焦点坐标是(0,-5),(0,5).
例题2
2.点M(x,y)到定点F(c,0)的距离和它到定直线:x=a^2/c的距离之比是常数c/a(c>a>0),
求点M的轨迹方程
解:设d是点M到直线l的距离,根据题意,
所求轨迹就是集合:
化简得:(c2-a2)x2-a2y2=a2(c2-a2).
双曲线的第二定义
平面内点M与一定点的距离和它到一条直线的距离的比是常数e=
叫做双曲线的准线,常数e是双曲线的离心率.
例题3
已知△ 的面积为 ,
(1)设 ,求 正切值的取值范围;
(2)设以O为中心,F为焦点的双曲线经过点Q(如图), 当
取得最小值时,求此双曲线的方程。
答案:
若双曲线
与直线 y=3^0.5x无交点,则离心率的取值范围是
A.(1,2) B.(1,2]
C.(1,5^0.5) D.( 1,5^0.5)
例题4
练习1
已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线 是 双曲线S 的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式·
成立.
(I)求双曲线S的方程;
(II)若双曲线S上存在两个点关于直线对称,求实数k的取值范围.
答案
练习2
已知双曲线 ,两点A(1,3),B(3,0),P为双曲线上的一点,则
|PA|+|PB|的最小值
练习3
(1)已知双曲线的半长轴为10,半短轴为8,
求双曲线的离心率与渐近线方程
(2)已知双曲线的半长轴为10,双曲线的离心率为2,
求渐近线方程
(3)已知双曲线的双曲线的离心率为3,半短轴为8,
求双曲线标准方程
曲线性质小结:
对于双曲线 ,相应于焦点(c,0)的准线方程是
x=a^2/c,根据双曲线的对称性,相应于焦点(-c,0)的准线方程是x= -a^2/c.
对于双曲线 ,相应于焦点(c,0)的准线方程
y=a^2/c,根据双曲线的对称性,相应于焦点(-c,0)的准线方程是y= -a^2/c.
总结:
1.双曲线发现过程
2.双曲线图像与椭圆图像的性质比较表格
3.双曲线综合问题
4.数学思想方法--------代数运算能力与数形结合思想
作业布置
课后习题AB组
THANGKS!!
双曲线的简单几何性质
复习提问引入新课
1.椭圆有哪些几何性质,是如何探讨的?
请一同学回答.应为:
范围、对称性、顶点、离心率,是从标准方程探讨的.
2.双曲线的两种标准方程是什么?
再请一同学回答.应为:
中心在原点、焦点在x轴上的双曲线的标
下面我们类比椭圆的几何性质来研究它的几何性质.
在学习椭圆时,以原点为中心,2a、2b为邻边的矩形,
对于估计椭圆的形状,画出椭圆的图形有很大的作用
仍以原点为中心,2a、2b为邻边作一矩形(板书图形),那么双曲线和这个矩形有什么关系?
这个矩形对于估计和画出双曲线简图(图2-26)有什么指导意义?这些问题不要求学生回答,只引起学生类比联想.
接着再提出问题:
当a、b为已知时,这个矩形的两条对角线的方程是什么?
请一个同学回答问题
应作出 ,并画出两条对角线,进一步引导学生从图观察得出结论:双曲线的各支向外延伸是,与这两条渐进线逐渐接近
椭圆与双曲线比较
双曲线在第一象限的部分可写成:
当x逐渐增大时,|MN|逐渐减小,x无限增大,|MN|接近于零,|MQ|也接近于零,就是说,双曲线在第一象限的部分从射线ON的下方逐渐接近于射线ON.
在其他象限内也可以证明类似的情况.
现在来看看实轴在y轴上的双曲线的渐近线方程是怎样的?由于焦点在y轴上的双曲线方程是由焦点在x轴上的双曲线方程,将x、y字母对换位置,所以双曲线
离心率
双曲线的离心率越大,
它的开口就越开阔.
焦点在y轴上的双曲线的几何性质可以类似得出,
双曲线的几何性质与坐标系的选择无关,
即不随坐标系的改变而改变.
1.双曲线的焦距与实轴的比e=c/a叫做双曲线的离心率,且e>1
例题1
求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
由此可知,实半轴长a=4,虚半轴长b=3.
焦点坐标是(0,-5),(0,5).
例题2
2.点M(x,y)到定点F(c,0)的距离和它到定直线:x=a^2/c的距离之比是常数c/a(c>a>0),
求点M的轨迹方程
解:设d是点M到直线l的距离,根据题意,
所求轨迹就是集合:
化简得:(c2-a2)x2-a2y2=a2(c2-a2).
双曲线的第二定义
平面内点M与一定点的距离和它到一条直线的距离的比是常数e=
叫做双曲线的准线,常数e是双曲线的离心率.
例题3
已知△ 的面积为 ,
(1)设 ,求 正切值的取值范围;
(2)设以O为中心,F为焦点的双曲线经过点Q(如图), 当
取得最小值时,求此双曲线的方程。
答案:
若双曲线
与直线 y=3^0.5x无交点,则离心率的取值范围是
A.(1,2) B.(1,2]
C.(1,5^0.5) D.( 1,5^0.5)
例题4
练习1
已知实轴长为2a,虚轴长为2b的双曲线S的焦点在x轴上,直线 是 双曲线S 的一条渐近线,而且原点O,点A(a,0)和点B(0,-b)使等式·
成立.
(I)求双曲线S的方程;
(II)若双曲线S上存在两个点关于直线对称,求实数k的取值范围.
答案
练习2
已知双曲线 ,两点A(1,3),B(3,0),P为双曲线上的一点,则
|PA|+|PB|的最小值
练习3
(1)已知双曲线的半长轴为10,半短轴为8,
求双曲线的离心率与渐近线方程
(2)已知双曲线的半长轴为10,双曲线的离心率为2,
求渐近线方程
(3)已知双曲线的双曲线的离心率为3,半短轴为8,
求双曲线标准方程
曲线性质小结:
对于双曲线 ,相应于焦点(c,0)的准线方程是
x=a^2/c,根据双曲线的对称性,相应于焦点(-c,0)的准线方程是x= -a^2/c.
对于双曲线 ,相应于焦点(c,0)的准线方程
y=a^2/c,根据双曲线的对称性,相应于焦点(-c,0)的准线方程是y= -a^2/c.
总结:
1.双曲线发现过程
2.双曲线图像与椭圆图像的性质比较表格
3.双曲线综合问题
4.数学思想方法--------代数运算能力与数形结合思想
作业布置
课后习题AB组
THANGKS!!
