人教A版数学选修2-1 2.2.1 椭圆及其标准方程 课件(共27张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.2.1 椭圆及其标准方程 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:16:22 | ||
图片预览








文档简介
(共27张PPT)
2.2.1 椭圆及其标准方程
历史回顾
两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;当平面再倾斜一些就可以得到双曲线。阿波罗尼曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。事实上,阿波罗尼在其著作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。
用一个平面去截一个圆锥面,得到的交线就称为圆锥曲线(conic sections)。
通常提到的圆锥曲线包括椭圆,双曲线和抛物线,但严格来讲,它还包括一些退化情形。具体而言:
1) 当平面与圆锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与圆锥面的母线平行,且过圆锥顶点,结果退化为一条直线。
3) 当平面只与圆锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直,结果为圆。
5) 当平面只与圆锥面一侧相交,且过圆锥顶点,结果退化为一个点。
6) 当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线)。
7) 当平面与圆锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
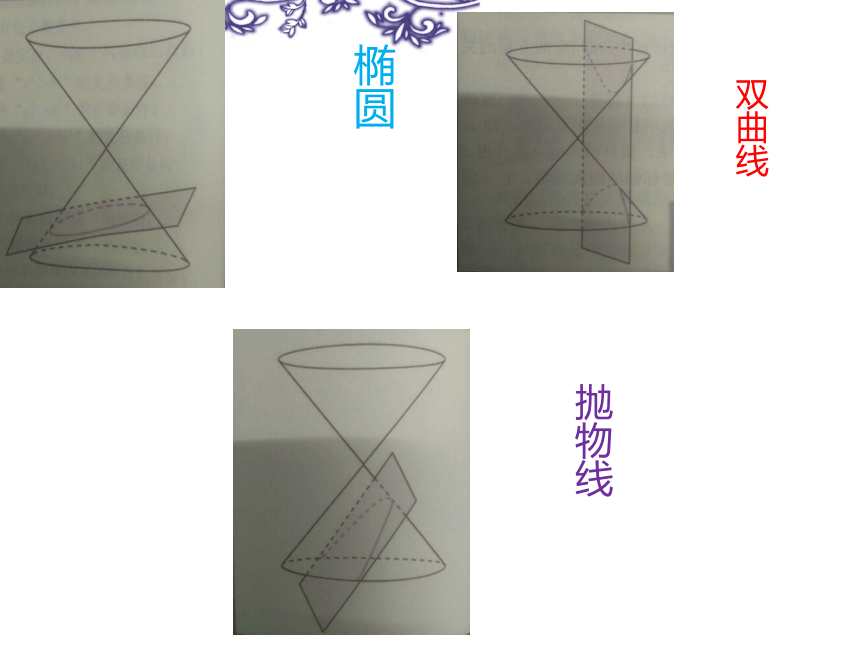
椭圆
双曲线
抛物线
举出生活中的椭圆
一、课题引入
1.圆的定义是什么?
平面内与一定点的距离等于定长的点的轨迹.
2.推导圆的方程
以圆心O为原点,建立直角坐标系
两边平方得 :
坐标法
设圆上任意一点
光学性质
从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上。
数 学 实 验
(1)取一条细绳,把它的两端固定在板上两点F1,F2;
(2)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形?
F1
F2
思考:如果我们将圆定义中的一个定点改变成两个定点,动点到定点距离的定长改变成动点到两定点的距离之和为定长。那么,将会形成什么样的轨迹曲线呢?
|F1F2|=2c(c>0);
|MF1|+|MF2|=2a(a>0);
F1
F2
M
探究1:椭圆的定义
若常数等于|F1F2|,则满足条件的点的轨迹是什么?
若常数小于|F1F2|,则满足条件的点的轨迹是什么?
线段|F1F2|
小结:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(1)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距离和为10,则M点的轨迹是什么
(2)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距
离和为6,则M点的轨迹是什么
(3)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距
离和为5,则M点的轨迹是什么
椭圆
线段|F1F2|
不存在
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
练习
化 简
列 式
设 点
建 系
建立适当平面直角坐标系
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
探究2:标准方程的推导(1)
F1
F2
M
0
x
y
从上述的过程可以看到,椭圆上任意一点的坐标都满足这个方程;
反过来,以这个方程的解(x,y)为坐标的点到椭圆的两个焦点F1(-c,0),F2(c,0)的距离之和为2a,即以这个方程的解为坐标的点都在椭圆上.
它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-c,0)、F2(c,0)
③ c2= a2 - b2
椭圆的标准方程⑴
F1
F2
M
0
x
y
观察下图,你能从中找出表示c,a, 的线段吗?(课本33页思考)
M
F1
F2
O
x
y
因为b2=a2-c2
所以
c
a
b
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢
椭圆的标准方程⑵
① 椭圆的焦点在y轴
② 焦点是F1(0,-c)、 F2(0,c)
③ c2= a2 - b2
x
M
F1
F2
y
O
它表示:
小结:椭圆的标准方程
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a(2a>2c)
分母哪个大,焦点就在哪个轴上
焦点位置的判断
例题1
【考点】椭圆的性质.菁优权所有
【专题】转化思想;转化法;圆锥曲线的定义、性质与方程;数学运算.
例题2
思考问题1
思考问题2
知识小结
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a(2a>2c)
分母哪个大,焦点就在哪个轴上
焦点位置的判断
数学思想归纳:
数形结合思想
分类讨论思想
作业:AB组
谢谢!
2.2.1 椭圆及其标准方程
历史回顾
两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;当平面再倾斜一些就可以得到双曲线。阿波罗尼曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。事实上,阿波罗尼在其著作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。
用一个平面去截一个圆锥面,得到的交线就称为圆锥曲线(conic sections)。
通常提到的圆锥曲线包括椭圆,双曲线和抛物线,但严格来讲,它还包括一些退化情形。具体而言:
1) 当平面与圆锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与圆锥面的母线平行,且过圆锥顶点,结果退化为一条直线。
3) 当平面只与圆锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直,结果为圆。
5) 当平面只与圆锥面一侧相交,且过圆锥顶点,结果退化为一个点。
6) 当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线)。
7) 当平面与圆锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
椭圆
双曲线
抛物线
举出生活中的椭圆
一、课题引入
1.圆的定义是什么?
平面内与一定点的距离等于定长的点的轨迹.
2.推导圆的方程
以圆心O为原点,建立直角坐标系
两边平方得 :
坐标法
设圆上任意一点
光学性质
从椭圆一个焦点发出的光,经过椭圆反射后,反射光线都汇聚到椭圆的另一个焦点上。
数 学 实 验
(1)取一条细绳,把它的两端固定在板上两点F1,F2;
(2)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形?
F1
F2
思考:如果我们将圆定义中的一个定点改变成两个定点,动点到定点距离的定长改变成动点到两定点的距离之和为定长。那么,将会形成什么样的轨迹曲线呢?
|F1F2|=2c(c>0);
|MF1|+|MF2|=2a(a>0);
F1
F2
M
探究1:椭圆的定义
若常数等于|F1F2|,则满足条件的点的轨迹是什么?
若常数小于|F1F2|,则满足条件的点的轨迹是什么?
线段|F1F2|
小结:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.
(1)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距离和为10,则M点的轨迹是什么
(2)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距
离和为6,则M点的轨迹是什么
(3)已知F1(-3,0),F2(3,0),M点到F1,F2两点的距
离和为5,则M点的轨迹是什么
椭圆
线段|F1F2|
不存在
(3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.
(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.
练习
化 简
列 式
设 点
建 系
建立适当平面直角坐标系
建立平面直角坐标系通常遵循的原则:“对称”、“简洁”
O
x
y
M
F1
F2
方案一
O
x
y
方案二
F1
F2
M
探究2:标准方程的推导(1)
F1
F2
M
0
x
y
从上述的过程可以看到,椭圆上任意一点的坐标都满足这个方程;
反过来,以这个方程的解(x,y)为坐标的点到椭圆的两个焦点F1(-c,0),F2(c,0)的距离之和为2a,即以这个方程的解为坐标的点都在椭圆上.
它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-c,0)、F2(c,0)
③ c2= a2 - b2
椭圆的标准方程⑴
F1
F2
M
0
x
y
观察下图,你能从中找出表示c,a, 的线段吗?(课本33页思考)
M
F1
F2
O
x
y
因为b2=a2-c2
所以
c
a
b
思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢
椭圆的标准方程⑵
① 椭圆的焦点在y轴
② 焦点是F1(0,-c)、 F2(0,c)
③ c2= a2 - b2
x
M
F1
F2
y
O
它表示:
小结:椭圆的标准方程
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a(2a>2c)
分母哪个大,焦点就在哪个轴上
焦点位置的判断
例题1
【考点】椭圆的性质.菁优权所有
【专题】转化思想;转化法;圆锥曲线的定义、性质与方程;数学运算.
例题2
思考问题1
思考问题2
知识小结
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
|MF1|+|MF2|=2a(2a>2c)
分母哪个大,焦点就在哪个轴上
焦点位置的判断
数学思想归纳:
数形结合思想
分类讨论思想
作业:AB组
谢谢!
