人教A版数学选修2-1 3.1.3 空间向量的数量积运算 课件(18张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 3.1.3 空间向量的数量积运算 课件(18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 867.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:27:43 | ||
图片预览





文档简介
(共18张PPT)
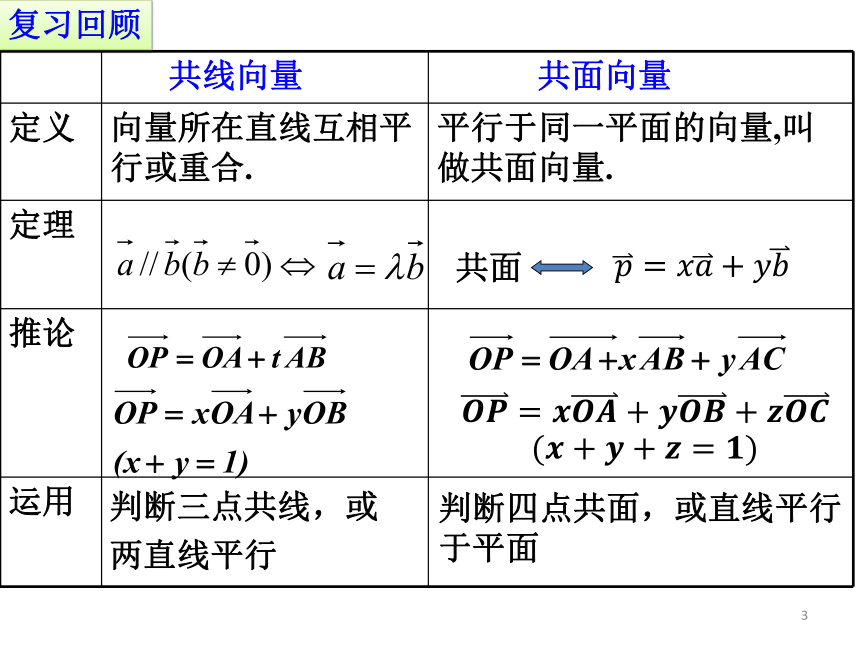
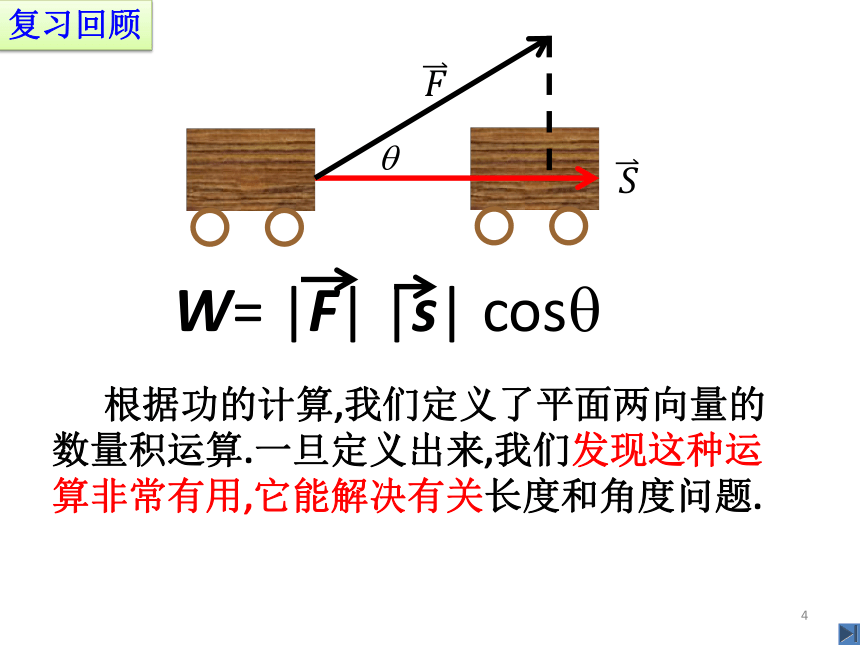
3.1空间向量及其运算3.1.3空间向量的数量积运算学习目标1.理解向量的夹角及空间向量的数量积运算概念;2.会运用公式解决立体几何中的有关问题;3.培养观察、分析、类比转化的能力;探究空间几何图形,将几何问题代数化.共线向量共面向量定义向量所在直线互相平行或重合.平行于同一平面的向量,叫做共面向量.定理推论运用共面复习回顾判断三点共线,或两直线平行判断四点共面,或直线平行于平面W= |F| |s| cos 根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.复习回顾在几何中,夹角和长度是两个最基本的几何量.下面我们探讨如何用空间向量的数量积表示空间两条直线的夹角和空间线段的长度.新课导入如图,已知两个非零向量 在空间任取一点O,作则∠AOB叫做向量,,的夹角,记作1.空间两个向量的夹角思考:夹角的范围是多大?〈,〉与〈,〉相等吗?,,,探究新知2.夹角的性质(1)范围:0≤〈,〉≤当〈,〉=0时,与同向;当〈,〉=时,与反向;当〈,〉=时,与垂直.(2)〈,〉=〈,〉注意:两个向量的夹角是唯一确定的!3.空间两个向量的数量积注意:②零向量与任意向量的数量积等于零③特别地,①两个向量的数量积是数量,而不是向量已知两个非零向量,,则,的数量积,记作.即=思考:类比平面向量,你能说出的几何意义吗?的模与在上的投影的乘积4.空间向量的数量积满足的运算律(1)(2)=(3)镶黄旗第一中学5.空间向量的数量积性质对于非零向量,设向量为单位向量,有以下性质:(1)(2);(3),也就是说;注意:性质(2)是证明两向量垂直的依据;性质(3)是求向量的长度(模)的依据,也是实数与向量之间转化的依据;性质(4)是解不等式的依据;性质(5)是求两个向量的夹角思考1.由=0,能否得到=或= 不一定,因为=,所以=0或=0或,即=或=或.思考2.对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量,由=,能得到吗?如果不能,请举出反例.不一定,例如向量与向量,都垂直时,有=,而未必有思考3.对于三个均不为0的数a,b,c,若ab=c,则a=或b=.对于向量若,能不能写成?也就是说,向量有除法吗?不能!因为向量没有除法.思考4.对于三个均不为0的数a,b,c,有.对于向量,,成立吗?不一定,两个向量的数量积为一个实数,表示与共线,表示与共线,而向量与向量的方向不确定,也就是说向量的数量积没有结合律.达标检测1.已知向量,满足=1,=2,=3,则=________.方法一:,代入已知条件求得=-2.,得=1.1方法二:+=2,代入已知条件求得=1.方法三:数形结合法,发现形的特殊性2.如图,在平行六面体中求 的长?解:因为,所以16+9+25+(0+10+7.5)85所以=
3.
B
当堂小结(1)空间两个向量的夹角的定义,记作(2)夹角的性质(取值范围和夹角的确定性)知识收获:(3)空间向量的数量积=(4)空间向量的数量积性质(5)空间向量的数量积性质(6)四个思考得出的空间向量数量积的特殊情况方法收获:类比转换法;向量法;数形结合法
3.1空间向量及其运算3.1.3空间向量的数量积运算学习目标1.理解向量的夹角及空间向量的数量积运算概念;2.会运用公式解决立体几何中的有关问题;3.培养观察、分析、类比转化的能力;探究空间几何图形,将几何问题代数化.共线向量共面向量定义向量所在直线互相平行或重合.平行于同一平面的向量,叫做共面向量.定理推论运用共面复习回顾判断三点共线,或两直线平行判断四点共面,或直线平行于平面W= |F| |s| cos 根据功的计算,我们定义了平面两向量的数量积运算.一旦定义出来,我们发现这种运算非常有用,它能解决有关长度和角度问题.复习回顾在几何中,夹角和长度是两个最基本的几何量.下面我们探讨如何用空间向量的数量积表示空间两条直线的夹角和空间线段的长度.新课导入如图,已知两个非零向量 在空间任取一点O,作则∠AOB叫做向量,,的夹角,记作1.空间两个向量的夹角思考:夹角的范围是多大?〈,〉与〈,〉相等吗?,,,探究新知2.夹角的性质(1)范围:0≤〈,〉≤当〈,〉=0时,与同向;当〈,〉=时,与反向;当〈,〉=时,与垂直.(2)〈,〉=〈,〉注意:两个向量的夹角是唯一确定的!3.空间两个向量的数量积注意:②零向量与任意向量的数量积等于零③特别地,①两个向量的数量积是数量,而不是向量已知两个非零向量,,则,的数量积,记作.即=思考:类比平面向量,你能说出的几何意义吗?的模与在上的投影的乘积4.空间向量的数量积满足的运算律(1)(2)=(3)镶黄旗第一中学5.空间向量的数量积性质对于非零向量,设向量为单位向量,有以下性质:(1)(2);(3),也就是说;注意:性质(2)是证明两向量垂直的依据;性质(3)是求向量的长度(模)的依据,也是实数与向量之间转化的依据;性质(4)是解不等式的依据;性质(5)是求两个向量的夹角思考1.由=0,能否得到=或= 不一定,因为=,所以=0或=0或,即=或=或.思考2.对于三个均不为0的数a,b,c,若ab=ac,则b=c.对于向量,由=,能得到吗?如果不能,请举出反例.不一定,例如向量与向量,都垂直时,有=,而未必有思考3.对于三个均不为0的数a,b,c,若ab=c,则a=或b=.对于向量若,能不能写成?也就是说,向量有除法吗?不能!因为向量没有除法.思考4.对于三个均不为0的数a,b,c,有.对于向量,,成立吗?不一定,两个向量的数量积为一个实数,表示与共线,表示与共线,而向量与向量的方向不确定,也就是说向量的数量积没有结合律.达标检测1.已知向量,满足=1,=2,=3,则=________.方法一:,代入已知条件求得=-2.,得=1.1方法二:+=2,代入已知条件求得=1.方法三:数形结合法,发现形的特殊性2.如图,在平行六面体中求 的长?解:因为,所以16+9+25+(0+10+7.5)85所以=
3.
B
当堂小结(1)空间两个向量的夹角的定义,记作(2)夹角的性质(取值范围和夹角的确定性)知识收获:(3)空间向量的数量积=(4)空间向量的数量积性质(5)空间向量的数量积性质(6)四个思考得出的空间向量数量积的特殊情况方法收获:类比转换法;向量法;数形结合法
