人教A版数学选修2-1 2.2.1 椭圆及其标准方程 课件(16张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.2.1 椭圆及其标准方程 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:29:16 | ||
图片预览






文档简介
(共16张PPT)
圆锥曲线起始课
——椭圆及其标准方程
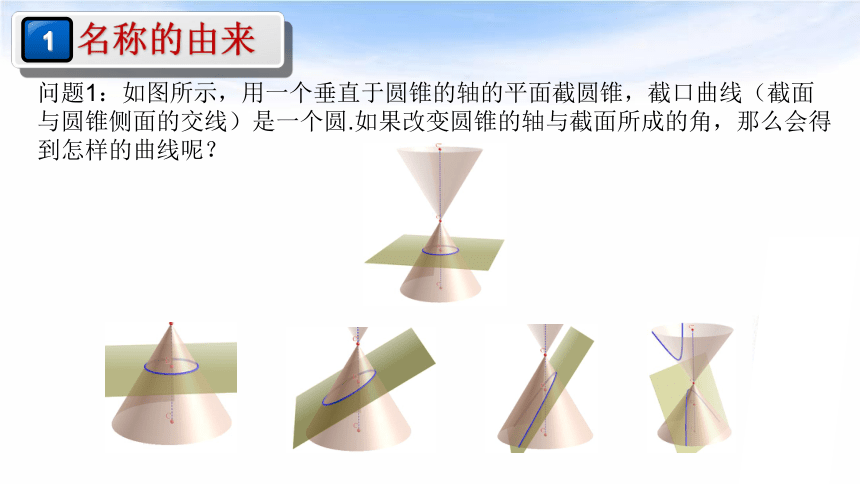
问题1:如图所示,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变圆锥的轴与截面所成的角,那么会得到怎样的曲线呢?
1
名称的由来
2
广泛的应用
开普勒
1571--1630
行星绕太阳运行的轨道是一个椭圆。
梅内克缪斯(公元前375年-公元前325年)
公元前4世纪,据说是古希腊数学家梅内克缪斯创造了抛物线、椭圆、双曲线这些术语,可惜没有留下任何著作.
阿波罗尼斯 (公元前262年-公元前190年)
公元前2世纪,古希腊数学家阿波罗尼斯在《圆锥曲线论》中深入而全面地研究了圆锥曲线的相关性质,对圆锥曲线的性质做了系统的研究(纯几何方法),并几乎网罗殆尽,使后人难以有新的发现.
17世纪初期,笛卡尔发明了坐标系,人们开始在坐标系的基础上,用代数的方法研究圆锥曲线.
笛卡尔 (1596年-1650年)
问题2:你能回顾用坐标法研究直线与圆的过程,给出研究圆锥曲线的大致步骤吗?
3
研究的路径
实际背景
曲线的
定义
曲线的方程
曲线的性质
实际应用
问题3:你在生活中见过椭圆形状的物品吗?
字典中的“椭圆”
如果把细绳的两端拉开一段距离,分别固定在图板的两点 ,如图所示,套上绳子,移动笔尖(始终保持绳子被拉紧的状态),画出的轨迹是什么曲线?在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
4
动手实践
问题4:类比圆的定义,请根据你的操作给出椭圆的定义?
5
椭圆的定义
现实背景
曲线的
定义
曲线的方程
曲线的性质
实际应用
M
F1
F2
6
椭圆的方程
建系
设点
列式
化简
验证
几何
代数
问题5:你能回顾并类比圆的方程的推导过程,给出建立椭圆的方程的大致步骤吗?
问题7:观察椭圆的形状,你认为怎样建立坐标系才能使椭圆的方程简单?并尝试建立椭圆的方程.
6
椭圆的方程
M
F1
F2
问题9:如图所示,如果焦点 在y轴上,且 的
坐标分别为 ,那么椭圆的方程是什么?
6
椭圆的方程
猜一猜
7
例题研讨
例1 已知椭圆的两个焦点坐标分别是 ,并且
经过点 ,求它的标准方程.
本节课学习了哪些知识?运用了哪些思想方法?觉得比较困难的地方是什么?
8
归纳小结
一个定义
两种方程
三类思想
平面上到两个定点 F1,F2 的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
焦点在 x轴上:
焦点在 y轴上:
数形结合思想
类比思想
方程思想
9
课后作业
1.课后作业题:教科书习题3.1 第1,2,6题
2.课后探究:观看微课“丹德林双球模型”,并撰写小论文《为什么截口曲线是椭圆》
再见!
圆锥曲线起始课
——椭圆及其标准方程
问题1:如图所示,用一个垂直于圆锥的轴的平面截圆锥,截口曲线(截面与圆锥侧面的交线)是一个圆.如果改变圆锥的轴与截面所成的角,那么会得到怎样的曲线呢?
1
名称的由来
2
广泛的应用
开普勒
1571--1630
行星绕太阳运行的轨道是一个椭圆。
梅内克缪斯(公元前375年-公元前325年)
公元前4世纪,据说是古希腊数学家梅内克缪斯创造了抛物线、椭圆、双曲线这些术语,可惜没有留下任何著作.
阿波罗尼斯 (公元前262年-公元前190年)
公元前2世纪,古希腊数学家阿波罗尼斯在《圆锥曲线论》中深入而全面地研究了圆锥曲线的相关性质,对圆锥曲线的性质做了系统的研究(纯几何方法),并几乎网罗殆尽,使后人难以有新的发现.
17世纪初期,笛卡尔发明了坐标系,人们开始在坐标系的基础上,用代数的方法研究圆锥曲线.
笛卡尔 (1596年-1650年)
问题2:你能回顾用坐标法研究直线与圆的过程,给出研究圆锥曲线的大致步骤吗?
3
研究的路径
实际背景
曲线的
定义
曲线的方程
曲线的性质
实际应用
问题3:你在生活中见过椭圆形状的物品吗?
字典中的“椭圆”
如果把细绳的两端拉开一段距离,分别固定在图板的两点 ,如图所示,套上绳子,移动笔尖(始终保持绳子被拉紧的状态),画出的轨迹是什么曲线?在这一过程中,移动的笔尖(动点)满足的几何条件是什么?
4
动手实践
问题4:类比圆的定义,请根据你的操作给出椭圆的定义?
5
椭圆的定义
现实背景
曲线的
定义
曲线的方程
曲线的性质
实际应用
M
F1
F2
6
椭圆的方程
建系
设点
列式
化简
验证
几何
代数
问题5:你能回顾并类比圆的方程的推导过程,给出建立椭圆的方程的大致步骤吗?
问题7:观察椭圆的形状,你认为怎样建立坐标系才能使椭圆的方程简单?并尝试建立椭圆的方程.
6
椭圆的方程
M
F1
F2
问题9:如图所示,如果焦点 在y轴上,且 的
坐标分别为 ,那么椭圆的方程是什么?
6
椭圆的方程
猜一猜
7
例题研讨
例1 已知椭圆的两个焦点坐标分别是 ,并且
经过点 ,求它的标准方程.
本节课学习了哪些知识?运用了哪些思想方法?觉得比较困难的地方是什么?
8
归纳小结
一个定义
两种方程
三类思想
平面上到两个定点 F1,F2 的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。
焦点在 x轴上:
焦点在 y轴上:
数形结合思想
类比思想
方程思想
9
课后作业
1.课后作业题:教科书习题3.1 第1,2,6题
2.课后探究:观看微课“丹德林双球模型”,并撰写小论文《为什么截口曲线是椭圆》
再见!
