人教A版数学选修2-1 2.2.2 椭圆的简单几何性质课件(2)(19张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 2.2.2 椭圆的简单几何性质课件(2)(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 483.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:31:57 | ||
图片预览






文档简介
(共19张PPT)
2.2.2椭圆的简单几何性质(2)
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
X
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点对称
关于x轴,y轴,原点对称
复习回顾
复习题
应用1:求椭圆离心率
1、若椭圆的焦距长等于它的短轴长,则其离心率为 。
2、若椭圆的两个焦点及一个短轴端点构成正三角形,则其离心率为 。
3、若椭圆的 的两个焦点把长轴分成三等分,则其离心率为 。
4、若某个椭圆的长轴、短轴、焦距依次成等差数列,
则其离心率e=__________
H
d
思考上面探究问题,并回答下列问题:
探究:
(1)用坐标法如何求出其轨迹方程,并说出轨迹
(2)给椭圆下一个新的定义
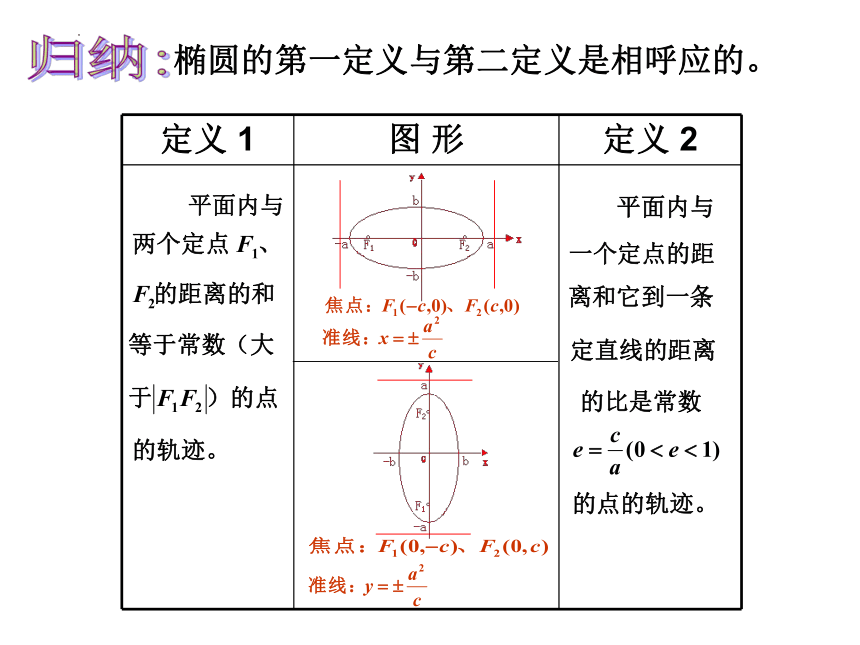
归纳:
椭圆的第一定义与第二定义是相呼应的。
定义 1 图 形 定义 2
平面内与
直线与椭圆的位置关系
直线与椭圆的位置关系
>
两解
一
=
无
<
直线与椭圆的位置关系
o
x
y
直线与椭圆的位置关系
弦长问题
弦长问题
中心弦问题
中心弦问题
点差法
中心弦问题
中心弦问题
中心弦问题
2、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;(韦达定理法)
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。(点差法)
1、直线与椭圆的三种位置关系及判断方法;
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3.弦长公式
课堂小结
2.2.2椭圆的简单几何性质(2)
方程
图形
范围
对称性
顶点
离心率
x
y
B1
B2
A1
A2
∣ ∣
F1 F2
Y
X
F1
O
F2
_
_
A2
A1
B1
B2
0
关于x轴,y轴,原点对称
关于x轴,y轴,原点对称
复习回顾
复习题
应用1:求椭圆离心率
1、若椭圆的焦距长等于它的短轴长,则其离心率为 。
2、若椭圆的两个焦点及一个短轴端点构成正三角形,则其离心率为 。
3、若椭圆的 的两个焦点把长轴分成三等分,则其离心率为 。
4、若某个椭圆的长轴、短轴、焦距依次成等差数列,
则其离心率e=__________
H
d
思考上面探究问题,并回答下列问题:
探究:
(1)用坐标法如何求出其轨迹方程,并说出轨迹
(2)给椭圆下一个新的定义
归纳:
椭圆的第一定义与第二定义是相呼应的。
定义 1 图 形 定义 2
平面内与
直线与椭圆的位置关系
直线与椭圆的位置关系
>
两解
一
=
无
<
直线与椭圆的位置关系
o
x
y
直线与椭圆的位置关系
弦长问题
弦长问题
中心弦问题
中心弦问题
点差法
中心弦问题
中心弦问题
中心弦问题
2、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;(韦达定理法)
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。(点差法)
1、直线与椭圆的三种位置关系及判断方法;
解方程组消去其中一元得一元二次型方程
△< 0 相离
△= 0 相切
△> 0 相交
3.弦长公式
课堂小结
