人教A版数学选修2-1 3.2 立体几何中的向量方法1 课件(65张PPT)
文档属性
| 名称 | 人教A版数学选修2-1 3.2 立体几何中的向量方法1 课件(65张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 16:34:29 | ||
图片预览










文档简介
(共65张PPT)
3.2立体几何中的向量方法学习目标
1.用向量表示空间中的点、直线和平面的位置;
2.用向量表示空间中直线、平面平行、垂直及夹角等;
3.利用空间向量求距离;
4.用向量方法解决立体几何问题的“三步曲”; 向量方
法与坐标方法结合解决立体几何问题.
重难点
重点:理解并掌握向量方法解决立体几何问题的一般方法
(“三步曲”);
难点:建立立体图形与空间向量之间的联系,把立体几何
问题转化为向量问题.
从上一节,我们把向量从平面推广到空间,
并利用空间向量解决了一些立体几何问题.你是否已经初步体会到空间向量在解决立体几何问题中的作用?这一节我们将进一步学习立体几何中的向量方法.
立体几何研究的基本对象是点、直线、平面以及它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来.
新课导入
思考1:
1.如何确定一个点在空间的位置?
2.在空间中给一个定点A和一个定方向(向量), 能确定一条直线在空间的位置吗?
3.给一个定点和两个定方向(向量),能确定一个平面在空间的位置吗?
4.给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗?
讲授新课
问题1.如何确定一个点在空间的位置?OP一、点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P的位置就可以用向量来表示.我们把向量称为点P的位置向量.ABP问题2.在空间中给一个定点A和一个定方向(向量),能确定一条直线在空间的位置吗?
二、直线的向量参数方程
空间中任意一条直线,可以通过上的一个定点A和的一
个方向向量来确定.设点P是上的任意一点,则有向量表
示形式,其中为实数,这种形式叫做直线的点向式
表示.注意:同一条直线的点向式表示并不唯一,例如直线
可以表示为,或,这里的是不同的实数
和是不同的向量,但是一定有.
此方程称为直线的向量参数方程.这样点A和向量不仅
可以确定直线的位置,还可以具体写出上的任意一点.
问题3.给一个定点和两个定方向(向量),
能确定一个平面在空间的位置吗?
空间中任意一个平面α,有两种向量表示形式:
(1)通过α上的一个定点O和两个向量和来确定.
空间中平面α的位置可以由α内两条相交直线来确定.设
这两条直线相交于点O,它们的方向向量分别为和,设
点P是α上的任意一点,则α有向量的表示形式,其中为实数,这种形式与平面向量基本定理一致.注意:同一个平面的这种形式的表达式并不唯一.例如,平面α可以表示为,或,这里的,,,.不完全相同.
这样点O和向量, 不仅可以确定平面α的位置,还可以具体表示出α上的任意一点.
(2)通过α上的一个定点O和一个向量来确定.
设点P是α上的任意一点,则α有向量表示形式=0,
其中是α的法向量,这种形式叫做平面的点法式表示.
注意:同一个平面的这种形式的表达式并不唯一.
例如:平面α可以表示为=0,或=0,这里的
和是不同的法向量,但法向量一定是非零向量,且一定
有.
问题4.给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗?
从以上可以看出,用空间向量确定点、直线、平面的位
置时,都需要事先确定某个定点,作为表达式中向量的起
点,例如以上所说的O,A等.所谓用空间向量确定点、直线、
平面的位置,即用空间向量形式可以表达空间中确定的点、
直线、平面.这样就能将立体几何问题转化为向量问题来讨论,这是学习用空间向量确定点、直线、平面的位置的目的.
想一想
1.如果另有一条直线,在直线上任取向量 ,与(是法向量)有什么关系
2.如何求平面的法向量?
共线
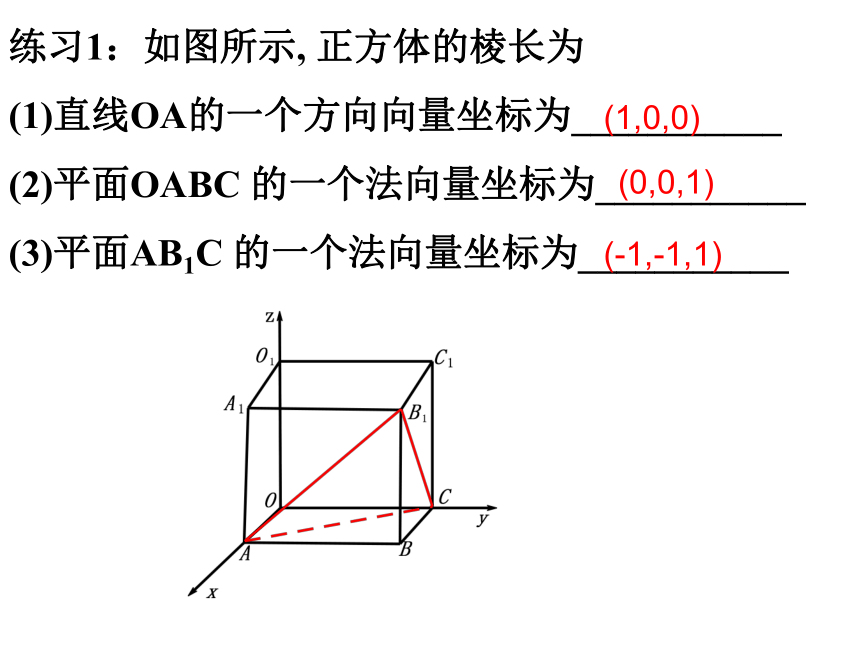
练习1:如图所示, 正方体的棱长为
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________
(-1,-1,1)
(0,0,1)
(1,0,0)
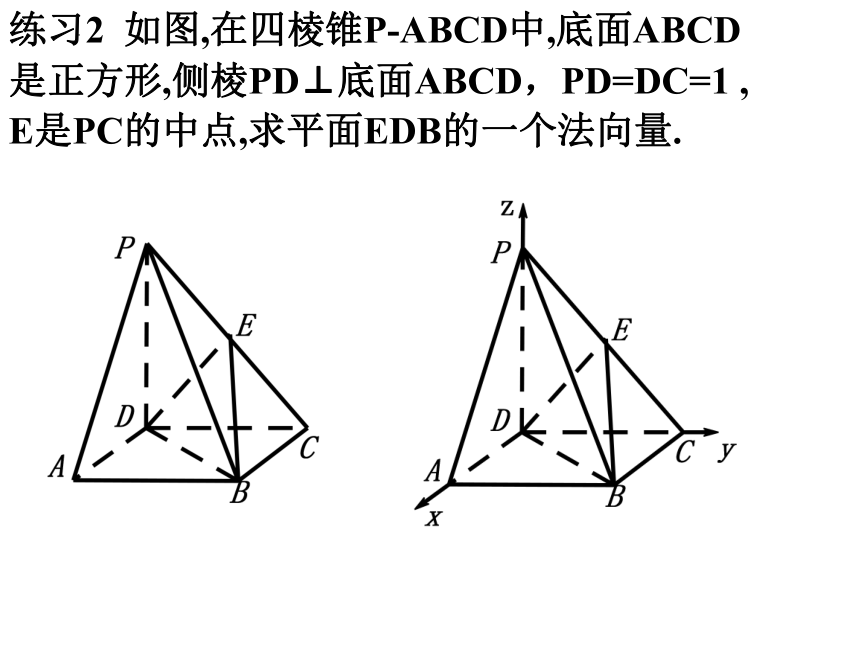
练习2 如图,在四棱锥P-ABCD中,底面ABCD
是正方形,侧棱PD⊥底面ABCD,PD=DC=1 ,
E是PC的中点,求平面EDB的一个法向量.
解:分别以为单位正交基底建立空间直角坐标系.
,
设平面EDB的法向量为
则,
是平面EDB的一个法向量
因为方向向量与法向量可以确定直线和
平面的位置,所以我们可以利用直线的方
向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系.
设直线的方向向量是=,平面α的法向量
,则
⊥ =0
0;
⊥
,
=, ,
探究
1.若直线和平面α所成的角为θ,你能用,表示θ吗?
2.你能用直线的方向向量表示空间两直线平行、垂直的位置关系以及它们之间的夹角吗?
3.你能用平面的法向量表示空间两平面平行、垂直的位置关系以及它们二面角的大小吗?
一般地,由直线、平面的位置关系以及直线的方
向向量和平面的法向量,可以归纳如下结论:
设直线的方向向量分别为,,平面α,β的法向量分别
为,,则:
线线平行
线面平行 ⊥ =0;
面面平行 α//β .
线线垂直 ⊥ ⊥ =0;
线面垂直 ⊥ , ;
面面垂直 α⊥β ⊥ =0.
线线所成角 的夹角为θ(0≤ θ ≤),;
线面所成角 的夹角为θ(0≤ θ ≤),;
面面所成角 ,β的夹角为θ(0≤ θ ≤),
注意:(1)线线平行包括线线重合,线面平行包括在面
内,面面平行包括面面重合
(2)线线夹角、线面夹角、面面夹角都是按照相
关定义给出的,即0≤ θ ≤.
排忧解难
1.直线的方向向量实质上是与直线平行的非零向量,它有无数多个,平面的法向量也就有无数个.
2.利用空间向量解决立体几何中的平行问题
(1)证明两条直线平行,只需证明这两条直线的方向
向量是共线向量,但要注意说明这两条直线不重合.
(2)证明线面平行的方法
①证明直线的方向向量与平面的法向量垂直,但
要说明直线不在平面内;
②证明能够在平面内找到一个向量与已知直线的
方向向量共线,也要说明直线不在平面内;
③利用共面向量定理,即证明直线的方向向量与
平面内的两个不共线向量是共面向量.同时要注意
强调直线不在平面内.
几个判定定理的证明
一、平面与平面平行的判定定理:一个平面内的两条相交直
线与另一个平面平行,则这两个平面平行
已知:直线和平面α,β,其中 α, 与相交,
// β, // β,求证α//β.
证明:设相交直线的方向向量分别为,,平面α,β的
法向量分别为,.
因为 // β, // β,所以⊥, ⊥.
所以 =0, =0.
因为 α, 且 与相交,所以α内任一直线的方向向
量可以表示为如下形式( x,y).
因为 ,即平面β的法线与平面α内
任一直线垂直.所以平面β的法向量也是平面α的法向量
即.
因此 α//β
二、直线与平面平行的判定定理:平面外一条直线与此平面
内的一条直线平行,则该直线与此平面平行.
已知:直线和平面α,其中 α, //
求证 //α.
证明:设相交直线的方向向量分别为,,平面α的法向量为.
因为 //,所以, ∈ .
因为 ⊥α , α 所以⊥,
因此 =0, = =0.
所以 //α
三、平面与平面垂直的判定定理:一个平面过另一
个平面的垂线,则这两个平面垂直.
已知:直线和平面α, β,其中,且⊥α,,求证α⊥ β.
证明:设相交直线的方向向量为,平面α, β的法向量分别为,.
因为 ⊥α,所以,, ∈ .
因为 ,所以=0
因此 =·0
所以 α⊥ β.
利用空间向量求距离1.点与点间的距离若A,B,则设直线的方向向量分别为,,平面α,β的法向量分别为,,则:2.点与直线间的距离3.点到面的距离
①据定义,求由点向面所引垂线段的长;
②利用法向量求点面距,设是平面α的法向量,
点A是平面α内任一点,点P在平面外,则点P到平面
α的距离
d
注意:线面距,面面距均可
转化为点面距离求解
利用空间向量求距离
4.异面直线的距离
①先确定两异面直线所在向量的坐标表示;
②设出它们共垂线的一个向量(此向量方向
不影响计算结果),由与两异面直线所在向量分
别垂直,得出的坐标表示;
③在异面直线上各找一个点(如E和F),算出
或的坐标,然后用公式
利用空间向量求距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1中点,求点E到直线A1B的距离.
点E到直线A1B的距离为
利用空间向量求点到直线的距离
证明:设正方体棱长为1,以 为单位正交 基底,建立如图所示坐标系D-xyz,
,
利用空间向量求点到面的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.
证明:设正方体棱长为1,以 为单位正交 基底,建立如图所示坐标系D-xyz,
,
设为面的法向量
由
得
又因为
所以到面A1BE的距离为
=
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离.
解:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为
D1C到面A1BE的距离.
仿上例求得D1C到面A1BE的距离为
利用空间向量求直线到面的距离
=
利用空间向量求面到面的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.
解1:∵面D1CB1∥面A1BD
∴D1到面A1BD的距离即
为面D1CB1到面A1BD的距离
平面的一个法向量为
且
=
利用空间向量求异面直线的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求异面直线D1B与A1E的距离.
,
设与,都垂直
由
得
又因为
所以到的距离为
=
作业:P104练习1,2
立体几何中的向量方法——“三步曲”
1.建立立体图形与空间向量的联系,用空间
向量表示问题中涉及的点、直线、平面,把立体几
何问题转化为向量问题;
2.通过向量运算,研究点、直线、平面之间的位置
关系以及它们之间距离和夹角等问题;
3.根据运算结果的几何意义来解释相关问题.
例题精讲
例1:如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点的三条棱长都相等,它们彼此的夹角都是60°,那么 (1)以这个顶点为端点的晶体的对角线的长与棱长有什么关系?
A1
B1
C1
D1
A
B
C
D
图1
解:如图1,设
化为向量问题
依据向量的加法法则,
进行向量运算
所以
回到图形问题
这个晶体的对角线 的长是棱长的 倍。
(2)晶体中相对的两个平面之间的距离是多少?(提示:求两个平行平面的距离,通常归结为求点到面间的距离)
A1
B1
C1
D1
A
B
C
D
H
分析:面面距离
回归图形
点面距离
向量的模
解:
∴ 所求的距离是
思考
1.本题中平行六面体的对角线的长与棱长有什么关系?
=
3+2
2
所以本题中平行六面体的对角线的长是棱长的倍
思考
2.如果一个平行六面体的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于α,那么由这个平行六面体的对角线的长可以确定棱长吗?
设以这个顶点为端点的对角线长为,棱长为
则
例2:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线(库底与水坝的交线)的距离AC和BD分别为和 ,CD的长为 ,AB的长为 .求库底与水坝所成二面角的余弦值.
解:如图,
化为向量问题
根据向量的加法法则
进行向量运算
于是,得
A
B
C
D
图3
所以
回到图形问题
库底与水坝所成二面角的余弦值为
设向量 与 的夹角为 , 就是库底与水坝所成的二面角.
因此
思考
1.本题中如果夹角可以测出,而AB未知,
其他条件不变,可以计算AB的长吗?
=
可以
思考
2.如果已知一个平行六面体的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间的余弦值吗?
设以顶点为端点的对角线长为,三条棱长分为
则
可以
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
是BB1,,CD中点,求证:
练习1:正方体
中,E、F分别
平面ADE.
证明:设正方体棱长为1, 为单位正交 基底,建立如图所示坐标系D-xyz,
所以
x
D1F
以
练习2:如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB, 已知AB=4,AC=6,BD=8,求CD的长.
B
A
C
D
解:
解得
例3 一块均匀的正三角形面的钢板的质量为50kg,在它的顶点处分别受力 ,每个力与同它相邻的三角形的两边之间的角都是600,且 ,这些钢板在这些力的作用下将会怎样运动?这三个力最小为多少时,才能提起这块钢板?
, ,
解:以点A为原点,平面ABC为xAy坐标平面,方向为y轴正方向,为y轴的单位长度,建立空间直角坐标系Axyz,
设力方向上的单位向量坐标为,由于与,
的夹角均为,利用向量的数量积运算,得
解得,
注意到向量是单位向量,
因此
于是
同理可得,
这样,它们的合力
由于
则需
解得
要提起这块钢板,设均为
所以要提起这块钢板,均要大于.
例4 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)
(3)求二面角C-PB-D的大小.
A
B
C
D
P
E
F
(1)求证:PA//平面EDB;
(思路:证明PA与平面EDB内一条直线平行)
A
B
C
D
P
E
X
Y
Z
G
解法1 立体几何法
连接AC交BD于点G,再连结GE.
A
B
C
D
P
E
X
Y
Z
G
解法2:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:连接AC,AC交BD于点G,连接EG
A
B
C
D
P
E
X
Y
Z
解法3:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:
解得 =-2,=1
则
即
共面
A
B
C
D
P
E
X
Y
Z
解法4:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:
设平面EDB的法向量为
则
由
(2)求证:平面;
(思路:证明PB与平面EFD内两条相交直线垂直)
由题意得:
又,
所以
由已知,且
所以
A
B
C
D
P
E
F
解法1 立体几何法:设DC=1,
(3)求二面角C-PB-D的大小
A
B
C
D
P
E
F
X
Y
Z
解法2 解:如图建立空间直角坐标系,设DC=1.
A
B
C
D
P
E
F
X
Y
Z
平面的一个法向量为:
解法3 如图所示建立空间直角坐标系,
设DC=1.
平面的一个法向量为:
G
课堂总结
知识总结:
1.用向量表示空间中的点、直线和平面的位置;
2.用向量表示空间中直线、平面平行、垂直及夹角等;
3.利用空间向量求距离;
4.用向量方法解决立体几何问题的“三步曲”; 向量方法与坐标方法结合解决立体几何问题.
方法收获:
向量法;数形结合法;坐标法;探究法
3.2立体几何中的向量方法学习目标
1.用向量表示空间中的点、直线和平面的位置;
2.用向量表示空间中直线、平面平行、垂直及夹角等;
3.利用空间向量求距离;
4.用向量方法解决立体几何问题的“三步曲”; 向量方
法与坐标方法结合解决立体几何问题.
重难点
重点:理解并掌握向量方法解决立体几何问题的一般方法
(“三步曲”);
难点:建立立体图形与空间向量之间的联系,把立体几何
问题转化为向量问题.
从上一节,我们把向量从平面推广到空间,
并利用空间向量解决了一些立体几何问题.你是否已经初步体会到空间向量在解决立体几何问题中的作用?这一节我们将进一步学习立体几何中的向量方法.
立体几何研究的基本对象是点、直线、平面以及它们组成的空间图形.为了用空间向量解决立体几何问题,首先必须把点、直线、平面的位置用向量表示出来.
新课导入
思考1:
1.如何确定一个点在空间的位置?
2.在空间中给一个定点A和一个定方向(向量), 能确定一条直线在空间的位置吗?
3.给一个定点和两个定方向(向量),能确定一个平面在空间的位置吗?
4.给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗?
讲授新课
问题1.如何确定一个点在空间的位置?OP一、点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P的位置就可以用向量来表示.我们把向量称为点P的位置向量.ABP问题2.在空间中给一个定点A和一个定方向(向量),能确定一条直线在空间的位置吗?
二、直线的向量参数方程
空间中任意一条直线,可以通过上的一个定点A和的一
个方向向量来确定.设点P是上的任意一点,则有向量表
示形式,其中为实数,这种形式叫做直线的点向式
表示.注意:同一条直线的点向式表示并不唯一,例如直线
可以表示为,或,这里的是不同的实数
和是不同的向量,但是一定有.
此方程称为直线的向量参数方程.这样点A和向量不仅
可以确定直线的位置,还可以具体写出上的任意一点.
问题3.给一个定点和两个定方向(向量),
能确定一个平面在空间的位置吗?
空间中任意一个平面α,有两种向量表示形式:
(1)通过α上的一个定点O和两个向量和来确定.
空间中平面α的位置可以由α内两条相交直线来确定.设
这两条直线相交于点O,它们的方向向量分别为和,设
点P是α上的任意一点,则α有向量的表示形式,其中为实数,这种形式与平面向量基本定理一致.注意:同一个平面的这种形式的表达式并不唯一.例如,平面α可以表示为,或,这里的,,,.不完全相同.
这样点O和向量, 不仅可以确定平面α的位置,还可以具体表示出α上的任意一点.
(2)通过α上的一个定点O和一个向量来确定.
设点P是α上的任意一点,则α有向量表示形式=0,
其中是α的法向量,这种形式叫做平面的点法式表示.
注意:同一个平面的这种形式的表达式并不唯一.
例如:平面α可以表示为=0,或=0,这里的
和是不同的法向量,但法向量一定是非零向量,且一定
有.
问题4.给一个定点和一个定方向(向量),能确定一个平面在空间的位置吗?
从以上可以看出,用空间向量确定点、直线、平面的位
置时,都需要事先确定某个定点,作为表达式中向量的起
点,例如以上所说的O,A等.所谓用空间向量确定点、直线、
平面的位置,即用空间向量形式可以表达空间中确定的点、
直线、平面.这样就能将立体几何问题转化为向量问题来讨论,这是学习用空间向量确定点、直线、平面的位置的目的.
想一想
1.如果另有一条直线,在直线上任取向量 ,与(是法向量)有什么关系
2.如何求平面的法向量?
共线
练习1:如图所示, 正方体的棱长为
直线OA的一个方向向量坐标为___________
平面OABC 的一个法向量坐标为___________
平面AB1C 的一个法向量坐标为___________
(-1,-1,1)
(0,0,1)
(1,0,0)
练习2 如图,在四棱锥P-ABCD中,底面ABCD
是正方形,侧棱PD⊥底面ABCD,PD=DC=1 ,
E是PC的中点,求平面EDB的一个法向量.
解:分别以为单位正交基底建立空间直角坐标系.
,
设平面EDB的法向量为
则,
是平面EDB的一个法向量
因为方向向量与法向量可以确定直线和
平面的位置,所以我们可以利用直线的方
向向量与平面的法向量表示空间直线、平面间的平行、垂直、夹角等位置关系.
设直线的方向向量是=,平面α的法向量
,则
⊥ =0
0;
⊥
,
=, ,
探究
1.若直线和平面α所成的角为θ,你能用,表示θ吗?
2.你能用直线的方向向量表示空间两直线平行、垂直的位置关系以及它们之间的夹角吗?
3.你能用平面的法向量表示空间两平面平行、垂直的位置关系以及它们二面角的大小吗?
一般地,由直线、平面的位置关系以及直线的方
向向量和平面的法向量,可以归纳如下结论:
设直线的方向向量分别为,,平面α,β的法向量分别
为,,则:
线线平行
线面平行 ⊥ =0;
面面平行 α//β .
线线垂直 ⊥ ⊥ =0;
线面垂直 ⊥ , ;
面面垂直 α⊥β ⊥ =0.
线线所成角 的夹角为θ(0≤ θ ≤),;
线面所成角 的夹角为θ(0≤ θ ≤),;
面面所成角 ,β的夹角为θ(0≤ θ ≤),
注意:(1)线线平行包括线线重合,线面平行包括在面
内,面面平行包括面面重合
(2)线线夹角、线面夹角、面面夹角都是按照相
关定义给出的,即0≤ θ ≤.
排忧解难
1.直线的方向向量实质上是与直线平行的非零向量,它有无数多个,平面的法向量也就有无数个.
2.利用空间向量解决立体几何中的平行问题
(1)证明两条直线平行,只需证明这两条直线的方向
向量是共线向量,但要注意说明这两条直线不重合.
(2)证明线面平行的方法
①证明直线的方向向量与平面的法向量垂直,但
要说明直线不在平面内;
②证明能够在平面内找到一个向量与已知直线的
方向向量共线,也要说明直线不在平面内;
③利用共面向量定理,即证明直线的方向向量与
平面内的两个不共线向量是共面向量.同时要注意
强调直线不在平面内.
几个判定定理的证明
一、平面与平面平行的判定定理:一个平面内的两条相交直
线与另一个平面平行,则这两个平面平行
已知:直线和平面α,β,其中 α, 与相交,
// β, // β,求证α//β.
证明:设相交直线的方向向量分别为,,平面α,β的
法向量分别为,.
因为 // β, // β,所以⊥, ⊥.
所以 =0, =0.
因为 α, 且 与相交,所以α内任一直线的方向向
量可以表示为如下形式( x,y).
因为 ,即平面β的法线与平面α内
任一直线垂直.所以平面β的法向量也是平面α的法向量
即.
因此 α//β
二、直线与平面平行的判定定理:平面外一条直线与此平面
内的一条直线平行,则该直线与此平面平行.
已知:直线和平面α,其中 α, //
求证 //α.
证明:设相交直线的方向向量分别为,,平面α的法向量为.
因为 //,所以, ∈ .
因为 ⊥α , α 所以⊥,
因此 =0, = =0.
所以 //α
三、平面与平面垂直的判定定理:一个平面过另一
个平面的垂线,则这两个平面垂直.
已知:直线和平面α, β,其中,且⊥α,,求证α⊥ β.
证明:设相交直线的方向向量为,平面α, β的法向量分别为,.
因为 ⊥α,所以,, ∈ .
因为 ,所以=0
因此 =·0
所以 α⊥ β.
利用空间向量求距离1.点与点间的距离若A,B,则设直线的方向向量分别为,,平面α,β的法向量分别为,,则:2.点与直线间的距离3.点到面的距离
①据定义,求由点向面所引垂线段的长;
②利用法向量求点面距,设是平面α的法向量,
点A是平面α内任一点,点P在平面外,则点P到平面
α的距离
d
注意:线面距,面面距均可
转化为点面距离求解
利用空间向量求距离
4.异面直线的距离
①先确定两异面直线所在向量的坐标表示;
②设出它们共垂线的一个向量(此向量方向
不影响计算结果),由与两异面直线所在向量分
别垂直,得出的坐标表示;
③在异面直线上各找一个点(如E和F),算出
或的坐标,然后用公式
利用空间向量求距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1中点,求点E到直线A1B的距离.
点E到直线A1B的距离为
利用空间向量求点到直线的距离
证明:设正方体棱长为1,以 为单位正交 基底,建立如图所示坐标系D-xyz,
,
利用空间向量求点到面的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求B1到面A1BE的距离.
证明:设正方体棱长为1,以 为单位正交 基底,建立如图所示坐标系D-xyz,
,
设为面的法向量
由
得
又因为
所以到面A1BE的距离为
=
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求D1C到面A1BE的距离.
解:∵D1C∥面A1BE
∴ D1到面A1BE的距离即为
D1C到面A1BE的距离.
仿上例求得D1C到面A1BE的距离为
利用空间向量求直线到面的距离
=
利用空间向量求面到面的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,求面A1DB与面D1CB1的距离.
解1:∵面D1CB1∥面A1BD
∴D1到面A1BD的距离即
为面D1CB1到面A1BD的距离
平面的一个法向量为
且
=
利用空间向量求异面直线的距离
如图,在正方体ABCD-A1B1C1D1中,棱长为1,E为D1C1的中点,求异面直线D1B与A1E的距离.
,
设与,都垂直
由
得
又因为
所以到的距离为
=
作业:P104练习1,2
立体几何中的向量方法——“三步曲”
1.建立立体图形与空间向量的联系,用空间
向量表示问题中涉及的点、直线、平面,把立体几
何问题转化为向量问题;
2.通过向量运算,研究点、直线、平面之间的位置
关系以及它们之间距离和夹角等问题;
3.根据运算结果的几何意义来解释相关问题.
例题精讲
例1:如图1:一个结晶体的形状为四棱柱,其中,以顶点A为端点的三条棱长都相等,它们彼此的夹角都是60°,那么 (1)以这个顶点为端点的晶体的对角线的长与棱长有什么关系?
A1
B1
C1
D1
A
B
C
D
图1
解:如图1,设
化为向量问题
依据向量的加法法则,
进行向量运算
所以
回到图形问题
这个晶体的对角线 的长是棱长的 倍。
(2)晶体中相对的两个平面之间的距离是多少?(提示:求两个平行平面的距离,通常归结为求点到面间的距离)
A1
B1
C1
D1
A
B
C
D
H
分析:面面距离
回归图形
点面距离
向量的模
解:
∴ 所求的距离是
思考
1.本题中平行六面体的对角线的长与棱长有什么关系?
=
3+2
2
所以本题中平行六面体的对角线的长是棱长的倍
思考
2.如果一个平行六面体的各条棱长都相等,并且以某一顶点为端点的各棱间的夹角都等于α,那么由这个平行六面体的对角线的长可以确定棱长吗?
设以这个顶点为端点的对角线长为,棱长为
则
例2:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处.从A,B到直线(库底与水坝的交线)的距离AC和BD分别为和 ,CD的长为 ,AB的长为 .求库底与水坝所成二面角的余弦值.
解:如图,
化为向量问题
根据向量的加法法则
进行向量运算
于是,得
A
B
C
D
图3
所以
回到图形问题
库底与水坝所成二面角的余弦值为
设向量 与 的夹角为 , 就是库底与水坝所成的二面角.
因此
思考
1.本题中如果夹角可以测出,而AB未知,
其他条件不变,可以计算AB的长吗?
=
可以
思考
2.如果已知一个平行六面体的各棱长和一条对角线的长,并且以同一顶点为端点的各棱间的夹角都相等,那么可以确定各棱之间的余弦值吗?
设以顶点为端点的对角线长为,三条棱长分为
则
可以
A1
x
D1
B1
A
D
B
C
C1
y
z
E
F
是BB1,,CD中点,求证:
练习1:正方体
中,E、F分别
平面ADE.
证明:设正方体棱长为1, 为单位正交 基底,建立如图所示坐标系D-xyz,
所以
x
D1F
以
练习2:如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB, 已知AB=4,AC=6,BD=8,求CD的长.
B
A
C
D
解:
解得
例3 一块均匀的正三角形面的钢板的质量为50kg,在它的顶点处分别受力 ,每个力与同它相邻的三角形的两边之间的角都是600,且 ,这些钢板在这些力的作用下将会怎样运动?这三个力最小为多少时,才能提起这块钢板?
, ,
解:以点A为原点,平面ABC为xAy坐标平面,方向为y轴正方向,为y轴的单位长度,建立空间直角坐标系Axyz,
设力方向上的单位向量坐标为,由于与,
的夹角均为,利用向量的数量积运算,得
解得,
注意到向量是单位向量,
因此
于是
同理可得,
这样,它们的合力
由于
则需
解得
要提起这块钢板,设均为
所以要提起这块钢板,均要大于.
例4 如图,在四棱锥P-ABCD中,底面ABCD是
正方形,侧棱PD⊥底面ABCD,PD=DC, E是PC的
中点,作EF⊥PB交PB于点F.
(1)求证:PA//平面EDB;
(2)
(3)求二面角C-PB-D的大小.
A
B
C
D
P
E
F
(1)求证:PA//平面EDB;
(思路:证明PA与平面EDB内一条直线平行)
A
B
C
D
P
E
X
Y
Z
G
解法1 立体几何法
连接AC交BD于点G,再连结GE.
A
B
C
D
P
E
X
Y
Z
G
解法2:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:连接AC,AC交BD于点G,连接EG
A
B
C
D
P
E
X
Y
Z
解法3:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:
解得 =-2,=1
则
即
共面
A
B
C
D
P
E
X
Y
Z
解法4:设,以 为单位正交 基底,建立如图所示坐标系D-xyz,
(1)证明:
设平面EDB的法向量为
则
由
(2)求证:平面;
(思路:证明PB与平面EFD内两条相交直线垂直)
由题意得:
又,
所以
由已知,且
所以
A
B
C
D
P
E
F
解法1 立体几何法:设DC=1,
(3)求二面角C-PB-D的大小
A
B
C
D
P
E
F
X
Y
Z
解法2 解:如图建立空间直角坐标系,设DC=1.
A
B
C
D
P
E
F
X
Y
Z
平面的一个法向量为:
解法3 如图所示建立空间直角坐标系,
设DC=1.
平面的一个法向量为:
G
课堂总结
知识总结:
1.用向量表示空间中的点、直线和平面的位置;
2.用向量表示空间中直线、平面平行、垂直及夹角等;
3.利用空间向量求距离;
4.用向量方法解决立体几何问题的“三步曲”; 向量方法与坐标方法结合解决立体几何问题.
方法收获:
向量法;数形结合法;坐标法;探究法
