【新课标】7.2.1定义与命题 课件(共23张PPT)
文档属性
| 名称 | 【新课标】7.2.1定义与命题 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 17:32:43 | ||
图片预览







文档简介
(共23张PPT)
7.2.1定义与命题
北师大版八年级上册
教学目标
1.了解定义、命题、真命题、假命题、定理的含义,会区分命题的条件和结论,了解判断命题真假的方法,通过实例感受证明的过程与格式.
2.初步感受公理化思想,并了解本套教科书所采用的基本事实.
情境导入
这个黑客终于被抓住了
是的,现如今网络和人工智能的高速发展,给我们的生活带来了便捷,但是……
情境导入
这个黑客是个小偷吧?
可能是喜欢穿黑衣服的贼
新知讲解
交流必须对某些名称和术语有共同的语言认识才能进行。
根据上面的情境,你能得出什么结论?
要对名称和术语的含义加以描述,作出明确规定。
证明时,为了交流的方便,必须对某些名称和术语形成共同的认识.为此,就要对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义
新知讲解
(1)具有中华人民共和国国籍的人,叫做中华人民共和国公民.
(2)两点之间线段的长度,叫做这两点之间的距离.
(3)无限不循环小数称为无理数.
(4)由不在同一直线上的若干线段首尾顺次连接所组成的平面图形叫做多边形.
(5)有两条边相等的三角形叫做等腰三角形.
议一议
(1)任何一个三角形一定有一个角是直角.
(2)对顶角相等.
(3)无论n为怎样的自然数,式子n2-n+11的值都是质数.
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(5)你喜欢数学吗?
(6)作线段AB=CD.
下列各语句中,哪些语句对事情作出了判断,哪些没有?
是提问,没有作出判断.
是一个操作,也没有作出判断.
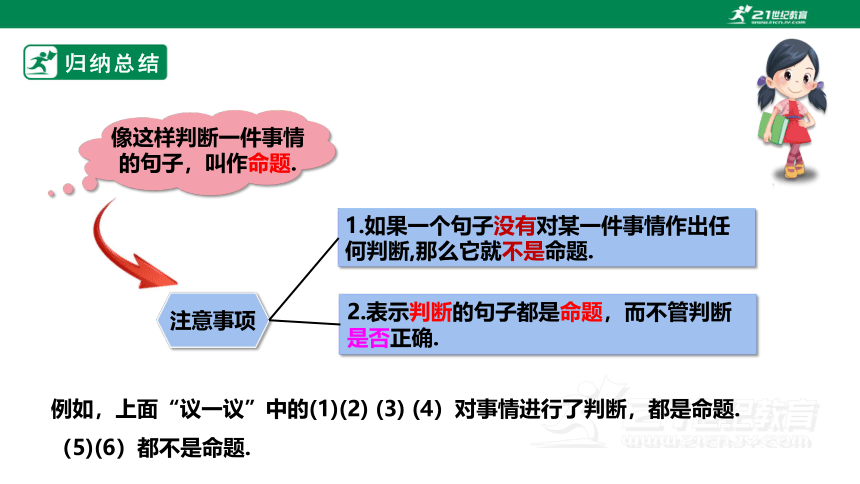
归纳总结
像这样判断一件事情的句子,叫作命题.
1.如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
2.表示判断的句子都是命题,而不管判断是否正确.
注意事项
例如,上面“议一议”中的(1)(2) (3) (4)对事情进行了判断,都是命题.
(5)(6)都不是命题.
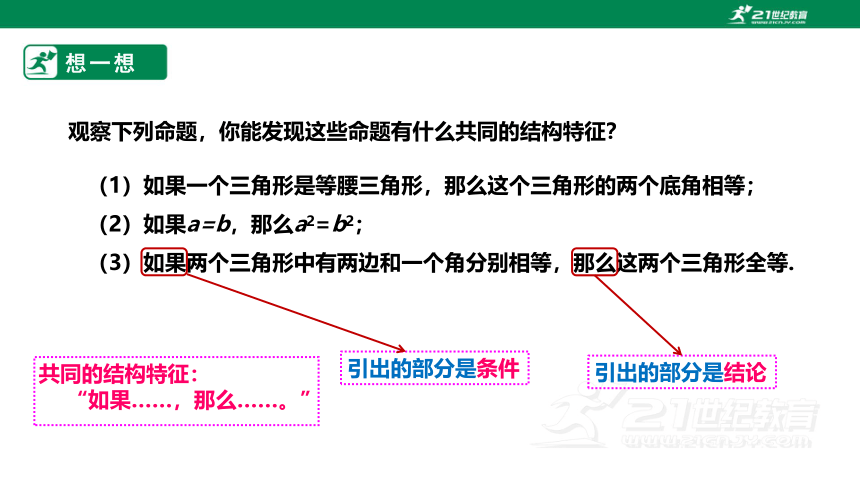
想一想
(1)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(2)如果a=b,那么a2=b2;
(3)如果两个三角形中有两边和一个角分别相等,那么这两个三角形全等.
观察下列命题,你能发现这些命题有什么共同的结构特征?
共同的结构特征:
“如果……,那么……。”
引出的部分是条件
引出的部分是结论
归纳小结
一般地,每个命题都由条件和结论两部分组成.
条件是已知的事项,结论是由已知事项推断出的事项.
命题通常可以写成“如果……那么……”的形式,
其中“如果”引出的部分是条件,“那么”引出的部分是结论.
典例精析
例、把下列命题改写成“如果……那么……”的形式.
如果一个三角形的一个角是直角,那么这个三角形是直角三角形.
如果两个角是同一个角的余角,那么这两个角相等.
如果一个角是锐角,那么这个角小于它的余角.
(1)有一个角是直角的三角形是直角三角形;
(2)同角的余角相等;
(3)锐角小于它的余角.
想一想
指出下列各命题的条件和结论,其中哪些命题是错误的?你是如何判断的?与同伴进行交流.
(1)如果两个角相等,那么它们是对顶角;
(2)如果a≠b,b≠c,那么a≠c;
(3)全等三角形的面积相等;
(4)如果室外气温低于0℃,那么地面上的水一定会结冰
归纳总结
正确的命题称为真命题,不正确的命题称为假命题.
要说明一个命题是假命题,常常可以举出一个例子,使它具备命题的条件,而不具有命题的结论,这种例子称为反例.
课堂练习
2.下列句子中不是命题的是( )
A.两直线平行,同位角相等
B.直线AB垂直于CD吗?
C.若|a|=|b|,则a2=b2
D.同角的补角相等
1.下列句子是定义的是( )
A.两点确定一条直线
B.同角或等角的余角相等
C.点到直线的距离是该点到这条直线的垂线段的长度
D.两直线平行,内错角相等
B
c
课堂练习
3.如果∠A>∠B,∠B>∠C,那么∠A>∠C.
这个命题的条件是 ,结论是 .
∠A>∠B,∠B>∠C
∠A>∠C
4.命题“锐角的补角是钝角”的题设为 ,
结论为 .
一个角是锐角的补角
这个角是钝角
课堂练习
5.下列命题的条件是什么 结论是什么
(1)如果两个三角形的两边及其夹角分别相等,那么这两个三角形全等;
(2)如果一个三角形中有两个角相等,那么这个三角形是等腰三角形;
(3)直角三角形的两锐角互余;
(4)两直线平行,同位角相等.
课堂练习
解:(1)条件是:两个三角形的两边及其夹角分别相等,结论是这两个三角形全等;
(2)条件:一个三角形中有两个角相等,结论:这个三角形是等腰三角形;
(3)条件:直角三角形的两锐角 结论:两锐角互余;
(4)条件:两直线平行 结论:同位角相等.
课堂练习
(1)一个角的补角大于这个角.
(2)已知三条线段a,b,c,如果a+b>c,那么这三条线段一定能组成三角形.
(3)有两角和一边相等的两个三角形全等.
解:(1)假命题.反例:150°角的补角是30°,显然不大于150°.
(2)假命题.反例:a=10,b=20,c=1,显然a+b>c,但这三条线段不能组成三角形.
(3)假命题.反例:在△ABC和△DEF中,∠A=∠D=90°,∠B=∠E=30°,AB=EF,则△ABC和△DEF不全等.
6.下列命题是真命题还是假命题?如果是假命题,请举出反例.
课堂总结
一、定义
概念
关键词:“叫做”“是”“称为”等
二、命题
概念
判断要点
作出判断
与是否正确无关
结构:
条件和结论
类型:
真命题和假命题
注意:语句通顺、不改题意
作用:准确找出条件和结论
三、改写命题
如果……那么……
形式:
板书设计
7.2.1定义与命题
1.定义的含义:对名称和术语的含义 加以描述,作出明确的规定,就是它们的定义;
2.命题的含义:判断一件事情的句子叫做命题,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题
3.命题的分类:真命题、假命题
作业布置
教材166页习题第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
7.2.1定义与命题
北师大版八年级上册
教学目标
1.了解定义、命题、真命题、假命题、定理的含义,会区分命题的条件和结论,了解判断命题真假的方法,通过实例感受证明的过程与格式.
2.初步感受公理化思想,并了解本套教科书所采用的基本事实.
情境导入
这个黑客终于被抓住了
是的,现如今网络和人工智能的高速发展,给我们的生活带来了便捷,但是……
情境导入
这个黑客是个小偷吧?
可能是喜欢穿黑衣服的贼
新知讲解
交流必须对某些名称和术语有共同的语言认识才能进行。
根据上面的情境,你能得出什么结论?
要对名称和术语的含义加以描述,作出明确规定。
证明时,为了交流的方便,必须对某些名称和术语形成共同的认识.为此,就要对名称和术语的含义加以描述,作出明确的规定,也就是给出它们的定义
新知讲解
(1)具有中华人民共和国国籍的人,叫做中华人民共和国公民.
(2)两点之间线段的长度,叫做这两点之间的距离.
(3)无限不循环小数称为无理数.
(4)由不在同一直线上的若干线段首尾顺次连接所组成的平面图形叫做多边形.
(5)有两条边相等的三角形叫做等腰三角形.
议一议
(1)任何一个三角形一定有一个角是直角.
(2)对顶角相等.
(3)无论n为怎样的自然数,式子n2-n+11的值都是质数.
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(5)你喜欢数学吗?
(6)作线段AB=CD.
下列各语句中,哪些语句对事情作出了判断,哪些没有?
是提问,没有作出判断.
是一个操作,也没有作出判断.
归纳总结
像这样判断一件事情的句子,叫作命题.
1.如果一个句子没有对某一件事情作出任何判断,那么它就不是命题.
2.表示判断的句子都是命题,而不管判断是否正确.
注意事项
例如,上面“议一议”中的(1)(2) (3) (4)对事情进行了判断,都是命题.
(5)(6)都不是命题.
想一想
(1)如果一个三角形是等腰三角形,那么这个三角形的两个底角相等;
(2)如果a=b,那么a2=b2;
(3)如果两个三角形中有两边和一个角分别相等,那么这两个三角形全等.
观察下列命题,你能发现这些命题有什么共同的结构特征?
共同的结构特征:
“如果……,那么……。”
引出的部分是条件
引出的部分是结论
归纳小结
一般地,每个命题都由条件和结论两部分组成.
条件是已知的事项,结论是由已知事项推断出的事项.
命题通常可以写成“如果……那么……”的形式,
其中“如果”引出的部分是条件,“那么”引出的部分是结论.
典例精析
例、把下列命题改写成“如果……那么……”的形式.
如果一个三角形的一个角是直角,那么这个三角形是直角三角形.
如果两个角是同一个角的余角,那么这两个角相等.
如果一个角是锐角,那么这个角小于它的余角.
(1)有一个角是直角的三角形是直角三角形;
(2)同角的余角相等;
(3)锐角小于它的余角.
想一想
指出下列各命题的条件和结论,其中哪些命题是错误的?你是如何判断的?与同伴进行交流.
(1)如果两个角相等,那么它们是对顶角;
(2)如果a≠b,b≠c,那么a≠c;
(3)全等三角形的面积相等;
(4)如果室外气温低于0℃,那么地面上的水一定会结冰
归纳总结
正确的命题称为真命题,不正确的命题称为假命题.
要说明一个命题是假命题,常常可以举出一个例子,使它具备命题的条件,而不具有命题的结论,这种例子称为反例.
课堂练习
2.下列句子中不是命题的是( )
A.两直线平行,同位角相等
B.直线AB垂直于CD吗?
C.若|a|=|b|,则a2=b2
D.同角的补角相等
1.下列句子是定义的是( )
A.两点确定一条直线
B.同角或等角的余角相等
C.点到直线的距离是该点到这条直线的垂线段的长度
D.两直线平行,内错角相等
B
c
课堂练习
3.如果∠A>∠B,∠B>∠C,那么∠A>∠C.
这个命题的条件是 ,结论是 .
∠A>∠B,∠B>∠C
∠A>∠C
4.命题“锐角的补角是钝角”的题设为 ,
结论为 .
一个角是锐角的补角
这个角是钝角
课堂练习
5.下列命题的条件是什么 结论是什么
(1)如果两个三角形的两边及其夹角分别相等,那么这两个三角形全等;
(2)如果一个三角形中有两个角相等,那么这个三角形是等腰三角形;
(3)直角三角形的两锐角互余;
(4)两直线平行,同位角相等.
课堂练习
解:(1)条件是:两个三角形的两边及其夹角分别相等,结论是这两个三角形全等;
(2)条件:一个三角形中有两个角相等,结论:这个三角形是等腰三角形;
(3)条件:直角三角形的两锐角 结论:两锐角互余;
(4)条件:两直线平行 结论:同位角相等.
课堂练习
(1)一个角的补角大于这个角.
(2)已知三条线段a,b,c,如果a+b>c,那么这三条线段一定能组成三角形.
(3)有两角和一边相等的两个三角形全等.
解:(1)假命题.反例:150°角的补角是30°,显然不大于150°.
(2)假命题.反例:a=10,b=20,c=1,显然a+b>c,但这三条线段不能组成三角形.
(3)假命题.反例:在△ABC和△DEF中,∠A=∠D=90°,∠B=∠E=30°,AB=EF,则△ABC和△DEF不全等.
6.下列命题是真命题还是假命题?如果是假命题,请举出反例.
课堂总结
一、定义
概念
关键词:“叫做”“是”“称为”等
二、命题
概念
判断要点
作出判断
与是否正确无关
结构:
条件和结论
类型:
真命题和假命题
注意:语句通顺、不改题意
作用:准确找出条件和结论
三、改写命题
如果……那么……
形式:
板书设计
7.2.1定义与命题
1.定义的含义:对名称和术语的含义 加以描述,作出明确的规定,就是它们的定义;
2.命题的含义:判断一件事情的句子叫做命题,如果一个句子没有对某一件事情作出任何判断,那么它就不是命题
3.命题的分类:真命题、假命题
作业布置
教材166页习题第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
