【新课标】4.4.4探索三角形相似的条件 课件(共21张PPT)
文档属性
| 名称 | 【新课标】4.4.4探索三角形相似的条件 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 14:57:49 | ||
图片预览







文档简介
(共21张PPT)
4.4.4探索三角形相似的条件
北师大版九年级上册
教学目标
1.理解并掌握黄金分割和黄金比的概念.
2.能利用黄金分割求线段的长.
复习旧知
什么是线段的比和比例线段?
两条线段的长度的比叫做两条线段的比.
四条线段a、b、c、d中,如果a与b的比等于c与d的比,
即 ,那么这四条线段a、b、c、d叫做成比例线段.
简称:比例线段.
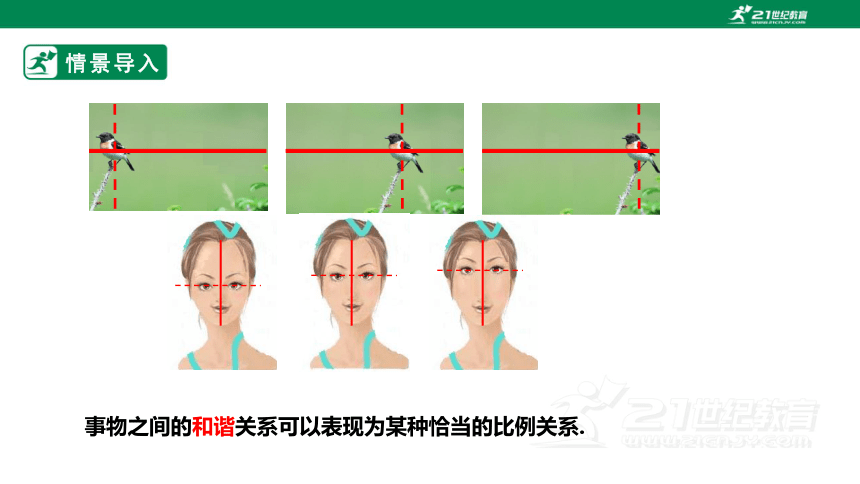
情景导入
通过观察,你觉得下面哪幅图最有美感?
情景导入
事物之间的和谐关系可以表现为某种恰当的比例关系.
新知讲解
一个五角星如图所示.
(1)从图中找出相等的角、相等的线段.
(2)在图中找出两对相似比不同的相似三角形.
小亮认为 ,
你同意他的看法吗?
说说你的理由.
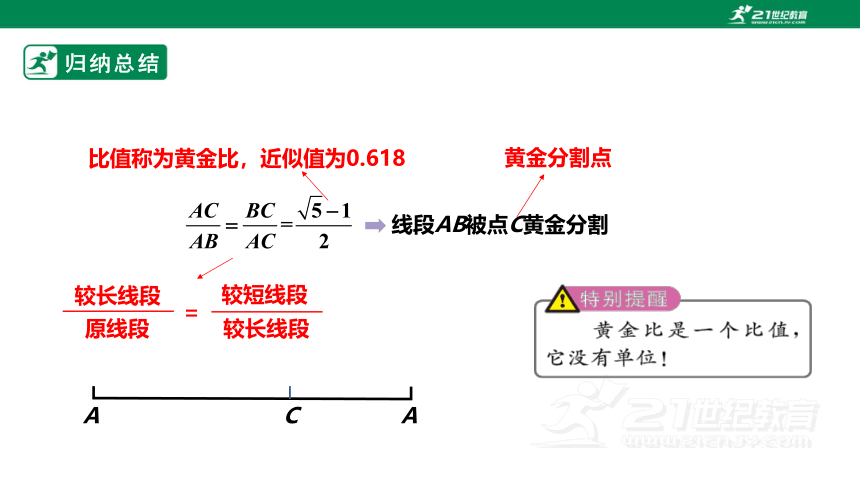
归纳总结
点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割. 点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
一条线段有几个黄金分割点?
2个
典例精析
A
A
C
例1.计算黄金比.
解:由,得AC2=AB·BC
设AB=1,AC=x,则BC=1-x .
∴ x2=1×(1-x)
即x2+x-1=0
解这个方程,得,
(不合题意,舍去)
所以,黄金比
归纳总结
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
A
A
C
归纳总结
C
A
B
∴ 点C是线段AB的黄金分割点
2.∵ 点C是线段AB的黄金分割
几何语言表示:
1.∵
∴
(判定)
(性质)
想一想
古希腊时期的巴台农神庙
A
B
D
C
E
F
图1
图2
如果把图1中用虚线表示的矩形画成图2中的 ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD.那么我们可以惊奇地发现.点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗
想一想
点E是AB的黄金分割点.
(即)是黄金比.
矩形ABCD的宽与长的比是黄金比.
宽与长的比等于黄金比的矩形也称为黄金矩形.
课堂练习
1.已知点C把线段AB分成两条线段AC,BC,下列说法错误的是( )
A.如果,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么AC与AB的比叫做黄金比
D.0.618是黄金比的近似值
C
课堂练习
2.已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形面积为S2,则S1与S2的关系是( )
A. S1 > S2 B. S1 < S2 C. S1 = S2 D. S1 ≥ S2
C
课堂练习
3.如果C是线段AB的黄金分割点,并且AC>CB,AB=1, 那么AC的长度为 .
4.在设计人体雕像时,使雕像的上部与下部的高度比等于下部与全身的高度比,可以增加视觉美感,按此比例,如果雕像的高为2m,设它的下部的高度应设计为xm,则x满足的关系为 .
(2-x)∶x=x∶2
课堂练习
5.黄金分割在生活中应用广泛,可以用于绘画、建筑等领域. 除此之外女孩子肚脐以下的身高如果和她的整个身高的比接近0.618时,越给人一种高挑、挺拔、匀称的美感. 有一个女孩身高165cm,下身身高100cm. 她应该穿高跟鞋吗?如果应该,她要穿多高的高跟鞋?(精确到1cm).
165cm
100cm
解:因为100÷165≈0.606小于黄金比,所有她应该穿高跟鞋.
设高跟鞋的高度为xcm,根据题意,得
解得:x≈5(cm)
所以她应该穿约5cm的高跟鞋.
课堂总结
黄金
分割
一条线段有两个黄金分割点.
黄金比:较长线段:原线段= :1
点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割. 点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
定义
板书设计
课题:4.4.4探索三角形相似的条件
一、定义:
二、黄金分割比:
作业布置
课本P98 习题4.8 第1,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
4.4.4探索三角形相似的条件
北师大版九年级上册
教学目标
1.理解并掌握黄金分割和黄金比的概念.
2.能利用黄金分割求线段的长.
复习旧知
什么是线段的比和比例线段?
两条线段的长度的比叫做两条线段的比.
四条线段a、b、c、d中,如果a与b的比等于c与d的比,
即 ,那么这四条线段a、b、c、d叫做成比例线段.
简称:比例线段.
情景导入
通过观察,你觉得下面哪幅图最有美感?
情景导入
事物之间的和谐关系可以表现为某种恰当的比例关系.
新知讲解
一个五角星如图所示.
(1)从图中找出相等的角、相等的线段.
(2)在图中找出两对相似比不同的相似三角形.
小亮认为 ,
你同意他的看法吗?
说说你的理由.
归纳总结
点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割. 点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.
一条线段有几个黄金分割点?
2个
典例精析
A
A
C
例1.计算黄金比.
解:由,得AC2=AB·BC
设AB=1,AC=x,则BC=1-x .
∴ x2=1×(1-x)
即x2+x-1=0
解这个方程,得,
(不合题意,舍去)
所以,黄金比
归纳总结
较长线段
原线段
=
较短线段
较长线段
比值称为黄金比,近似值为0.618
线段AB被点C黄金分割
黄金分割点
A
A
C
归纳总结
C
A
B
∴ 点C是线段AB的黄金分割点
2.∵ 点C是线段AB的黄金分割
几何语言表示:
1.∵
∴
(判定)
(性质)
想一想
古希腊时期的巴台农神庙
A
B
D
C
E
F
图1
图2
如果把图1中用虚线表示的矩形画成图2中的 ABCD,以矩形ABCD的宽为边在其内部作正方形AEFD.那么我们可以惊奇地发现.点E是AB的黄金分割点吗?矩形ABCD的宽与长的比是黄金比吗
想一想
点E是AB的黄金分割点.
(即)是黄金比.
矩形ABCD的宽与长的比是黄金比.
宽与长的比等于黄金比的矩形也称为黄金矩形.
课堂练习
1.已知点C把线段AB分成两条线段AC,BC,下列说法错误的是( )
A.如果,那么线段AB被点C黄金分割
B.如果AC2=AB·BC,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么AC与AB的比叫做黄金比
D.0.618是黄金比的近似值
C
课堂练习
2.已知线段AB,点P是它的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形面积为S2,则S1与S2的关系是( )
A. S1 > S2 B. S1 < S2 C. S1 = S2 D. S1 ≥ S2
C
课堂练习
3.如果C是线段AB的黄金分割点,并且AC>CB,AB=1, 那么AC的长度为 .
4.在设计人体雕像时,使雕像的上部与下部的高度比等于下部与全身的高度比,可以增加视觉美感,按此比例,如果雕像的高为2m,设它的下部的高度应设计为xm,则x满足的关系为 .
(2-x)∶x=x∶2
课堂练习
5.黄金分割在生活中应用广泛,可以用于绘画、建筑等领域. 除此之外女孩子肚脐以下的身高如果和她的整个身高的比接近0.618时,越给人一种高挑、挺拔、匀称的美感. 有一个女孩身高165cm,下身身高100cm. 她应该穿高跟鞋吗?如果应该,她要穿多高的高跟鞋?(精确到1cm).
165cm
100cm
解:因为100÷165≈0.606小于黄金比,所有她应该穿高跟鞋.
设高跟鞋的高度为xcm,根据题意,得
解得:x≈5(cm)
所以她应该穿约5cm的高跟鞋.
课堂总结
黄金
分割
一条线段有两个黄金分割点.
黄金比:较长线段:原线段= :1
点C把线段AB分成两条线段AC和BC,如果,那么称线段AB被点C黄金分割. 点C叫做线段AB的黄金分割点,AC与AB的比称为黄金比.
定义
板书设计
课题:4.4.4探索三角形相似的条件
一、定义:
二、黄金分割比:
作业布置
课本P98 习题4.8 第1,3,4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
