苏教版(2019)高中数学必修第二册 13.1.1_棱柱、棱锥和棱台_练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 13.1.1_棱柱、棱锥和棱台_练习(解析版) |
|
|
| 格式 | docx | ||
| 文件大小 | 356.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 21:47:10 | ||
图片预览



文档简介
第十三章 立体几何初步
13.1.1 棱柱、棱锥和棱台
一、选择题
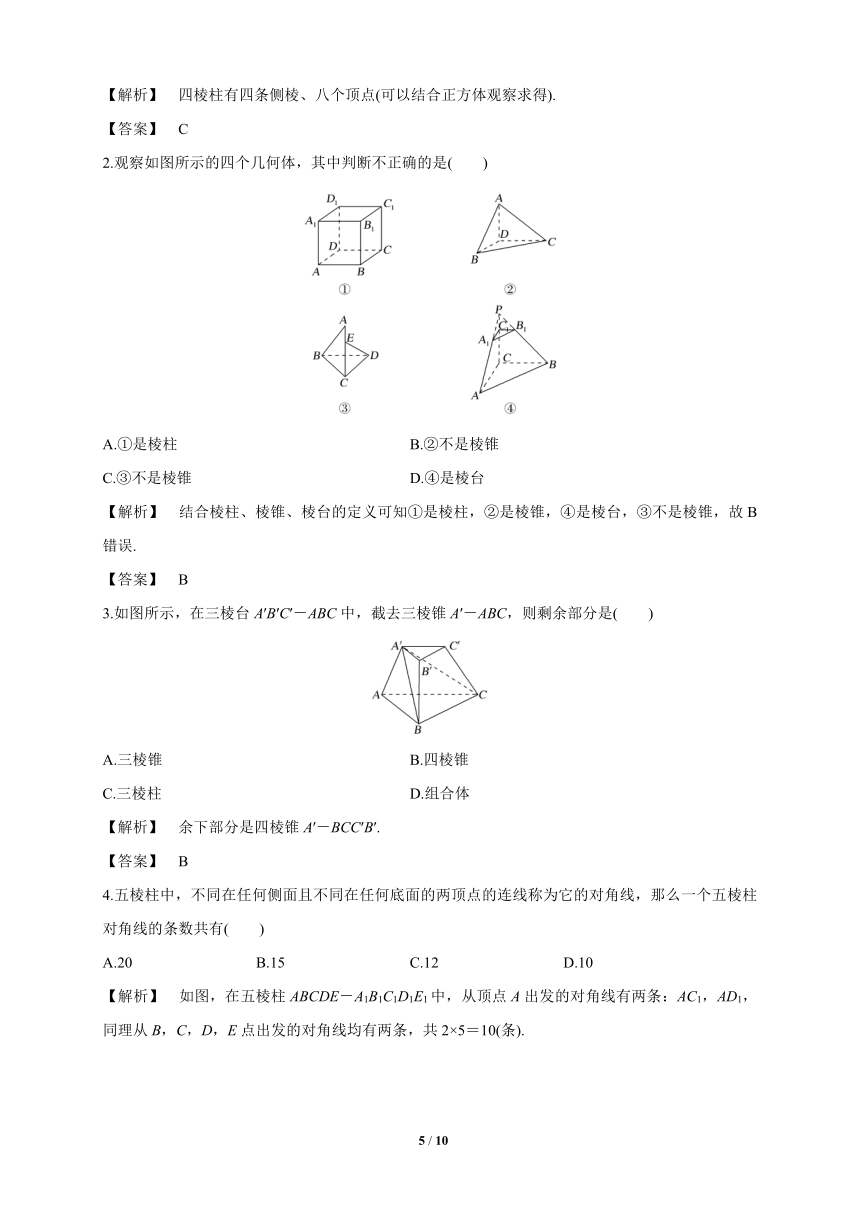
1.四棱柱有几条侧棱,几个顶点( )
A.四条侧棱、四个顶点 B.八条侧棱、四个顶点
C.四条侧棱、八个顶点 D.六条侧棱、八个顶点
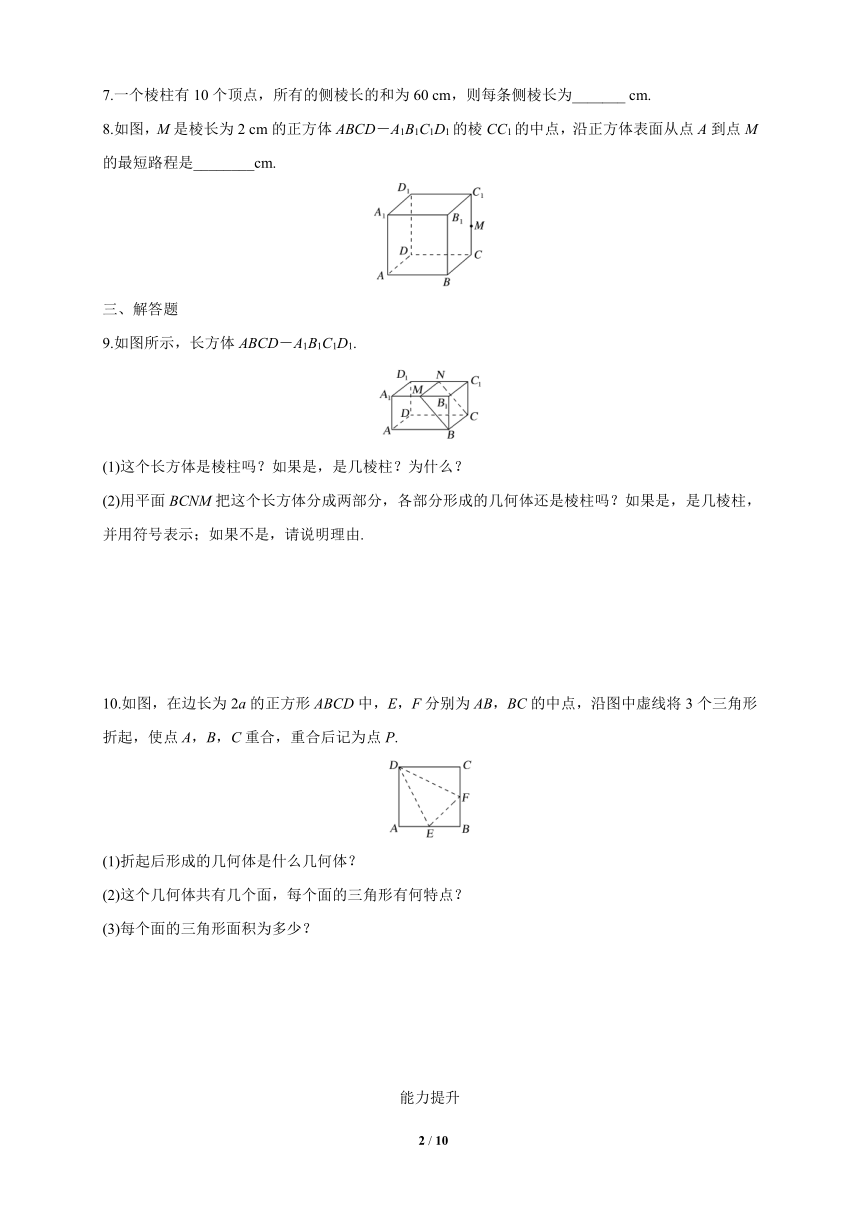
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
5.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
二、填空题
6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
7.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_______ cm.
8.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
三、解答题
9.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
能力提升
11.从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确结论的个数为________.
12.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
创新猜想
13.(多填题、开放题)如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________.
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(答案不唯一).
14.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.
第十三章 立体几何初步
13.1.1 棱柱、棱锥和棱台答案
一、选择题
1.四棱柱有几条侧棱,几个顶点( )
A.四条侧棱、四个顶点 B.八条侧棱、四个顶点
C.四条侧棱、八个顶点 D.六条侧棱、八个顶点
【解析】 四棱柱有四条侧棱、八个顶点(可以结合正方体观察求得).
【答案】 C
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
【解析】 结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.
【答案】 B
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
【解析】 余下部分是四棱锥A′-BCC′B′.
【答案】 B
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
【解析】 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共2×5=10(条).
【答案】 D
5.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
【解析】 由于棱锥的侧棱不一定相等,所以棱台的侧棱都相等的说法是错误的.
【答案】 C
二、填空题
6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
【解析】 由棱台的结构特征知,棱台上、下底面是相似多边形,面积比为对应边之比的平方.
【答案】 1∶4
7.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_______ cm.
【解析】 因棱柱有10个顶点,所以该棱柱为五棱柱,共有五条侧棱,所以侧棱长为=12(cm).
【答案】 12
8.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
【解析】 由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是 cm.故沿正方体表面从点A到点M的最短路程是
cm.
【答案】
三、解答题
9.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
解 (1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义.
(2)截面BCNM的上方部分是三棱柱BB1M-CC1N,下方部分是四棱柱ABMA1-DCND1.
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
解 (1)如图,折起后的几何体是三棱锥.
(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.
(3)S△PEF=a2,
S△DPF=S△DPE=×2a×a=a2,
S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE
=(2a)2-a2-a2-a2=a2.
能力提升
11.从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确结论的个数为________.
【解析】 如图所示:四边形ABCD为矩形,故(1)满足条件;四面体D-A1BC1为每个面均为等边三角形的四面体,故(2)满足条件;四面体D-B1C1D1为每个面都是直角三角形的四面体,故(3)满足条件;四面体C-B1C1D1为有三个面是等腰直角三角形,有一个面是等边三角形的四面体,故(4)满足条件;故正确的结论有4个.故【答案】为4.
【答案】 4
12.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.
∴△AEF周长的最小值为4.
创新猜想
13.(多填题、开放题)如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________.
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(【答案】不唯一).
【解析】 (1)如图①所示,所截成的三个三棱锥分别是A1-ABC,A1-BB1C1,A1-BCC1.
图①
(2)用平行于三棱台的底面的平面去截,可以得到两个三棱台,也可以截成一个三棱柱和一个五面体,如图②所示,也可以截成一个三棱锥和一个五面体,如图③所示.
图② 图③
【答案】 (1)A1-ABC,A1-BB1C1,A1-BCC1 (2)两个三棱台(或一个三棱柱和一个五面体或一个三棱锥和一个五面体)
14.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.
解 如图(1)所示,沿正三角形三边中点连线折起,可拼得一个底面为正三角形的三棱锥.
如图(2)所示,在正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的,有一组对角为直角,余下部分按虚线折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底.
4 / 10
13.1.1 棱柱、棱锥和棱台
一、选择题
1.四棱柱有几条侧棱,几个顶点( )
A.四条侧棱、四个顶点 B.八条侧棱、四个顶点
C.四条侧棱、八个顶点 D.六条侧棱、八个顶点
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
5.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
二、填空题
6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
7.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_______ cm.
8.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
三、解答题
9.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
能力提升
11.从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确结论的个数为________.
12.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
创新猜想
13.(多填题、开放题)如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________.
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(答案不唯一).
14.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.
第十三章 立体几何初步
13.1.1 棱柱、棱锥和棱台答案
一、选择题
1.四棱柱有几条侧棱,几个顶点( )
A.四条侧棱、四个顶点 B.八条侧棱、四个顶点
C.四条侧棱、八个顶点 D.六条侧棱、八个顶点
【解析】 四棱柱有四条侧棱、八个顶点(可以结合正方体观察求得).
【答案】 C
2.观察如图所示的四个几何体,其中判断不正确的是( )
A.①是棱柱 B.②不是棱锥
C.③不是棱锥 D.④是棱台
【解析】 结合棱柱、棱锥、棱台的定义可知①是棱柱,②是棱锥,④是棱台,③不是棱锥,故B错误.
【答案】 B
3.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
【解析】 余下部分是四棱锥A′-BCC′B′.
【答案】 B
4.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
【解析】 如图,在五棱柱ABCDE-A1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共2×5=10(条).
【答案】 D
5.棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱都相等 D.侧棱延长后都交于一点
【解析】 由于棱锥的侧棱不一定相等,所以棱台的侧棱都相等的说法是错误的.
【答案】 C
二、填空题
6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是________.
【解析】 由棱台的结构特征知,棱台上、下底面是相似多边形,面积比为对应边之比的平方.
【答案】 1∶4
7.一个棱柱有10个顶点,所有的侧棱长的和为60 cm,则每条侧棱长为_______ cm.
【解析】 因棱柱有10个顶点,所以该棱柱为五棱柱,共有五条侧棱,所以侧棱长为=12(cm).
【答案】 12
8.如图,M是棱长为2 cm的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是________cm.
【解析】 由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2 cm,3 cm,故两点之间的距离是 cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是 cm.故沿正方体表面从点A到点M的最短路程是
cm.
【答案】
三、解答题
9.如图所示,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗?如果是,是几棱柱?为什么?
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
解 (1)是棱柱,并且是四棱柱,因为长方体相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义.
(2)截面BCNM的上方部分是三棱柱BB1M-CC1N,下方部分是四棱柱ABMA1-DCND1.
10.如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
(1)折起后形成的几何体是什么几何体?
(2)这个几何体共有几个面,每个面的三角形有何特点?
(3)每个面的三角形面积为多少?
解 (1)如图,折起后的几何体是三棱锥.
(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.
(3)S△PEF=a2,
S△DPF=S△DPE=×2a×a=a2,
S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE
=(2a)2-a2-a2-a2=a2.
能力提升
11.从正方体ABCD-A1B1C1D1的8个顶点中任意取4个不同的顶点,这4个顶点可能是:
(1)矩形的4个顶点;(2)每个面都是等边三角形的四面体的4个顶点;(3)每个面都是直角三角形的四面体的4个顶点;(4)有三个面是等腰直角三角形,有一个面是等边三角形的四面体的4个顶点.
其中正确结论的个数为________.
【解析】 如图所示:四边形ABCD为矩形,故(1)满足条件;四面体D-A1BC1为每个面均为等边三角形的四面体,故(2)满足条件;四面体D-B1C1D1为每个面都是直角三角形的四面体,故(3)满足条件;四面体C-B1C1D1为有三个面是等腰直角三角形,有一个面是等边三角形的四面体,故(4)满足条件;故正确的结论有4个.故【答案】为4.
【答案】 4
12.如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
解 将三棱锥沿侧棱VA剪开,并将其侧面展开平铺在一个平面上,如图,线段AA1的长为所求△AEF周长的最小值.
∵∠AVB=∠A1VC=∠BVC=30°,∴∠AVA1=90°.
又VA=VA1=4,∴AA1=4.
∴△AEF周长的最小值为4.
创新猜想
13.(多填题、开放题)如图所示的是一个三棱台ABC-A1B1C1,
(1)如果把这个三棱台截成三个三棱锥,则这三个三棱锥分别是________________.
(2)如果把这个三棱台截成两个多面体,则这两个多面体可以是__________(【答案】不唯一).
【解析】 (1)如图①所示,所截成的三个三棱锥分别是A1-ABC,A1-BB1C1,A1-BCC1.
图①
(2)用平行于三棱台的底面的平面去截,可以得到两个三棱台,也可以截成一个三棱柱和一个五面体,如图②所示,也可以截成一个三棱锥和一个五面体,如图③所示.
图② 图③
【答案】 (1)A1-ABC,A1-BB1C1,A1-BCC1 (2)两个三棱台(或一个三棱柱和一个五面体或一个三棱锥和一个五面体)
14.给出两块正三角形纸片(如图所示),要求将其中一块剪拼成一个底面为正三角形的三棱锥模型,另一块剪拼成一个底面是正三角形的三棱柱模型,请设计一种剪拼方案,分别用虚线标示在图中,并作简要说明.
解 如图(1)所示,沿正三角形三边中点连线折起,可拼得一个底面为正三角形的三棱锥.
如图(2)所示,在正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的,有一组对角为直角,余下部分按虚线折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底.
4 / 10
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
