2022-2023学年人教版八年级数学下册16.2.2 二次根式的除法 课件(共18张PPT)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册16.2.2 二次根式的除法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第16.2.2 二次根式的除法
人教版数学八年级下册
学习目标
1.了解二次根式的除法法则.
2.会运用除法法则及商的算术平方根进行简单运算.
3.能将二次根式化为最简二次根式.
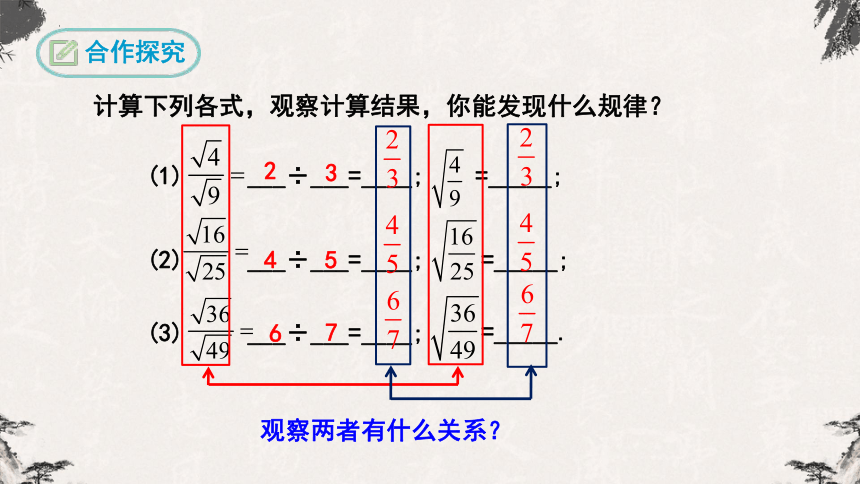
计算下列各式,观察计算结果,你能发现什么规律?
合作探究
(1) ___÷___=____;
=_____;
(2) ___÷___=____;
(3) ___÷___=____;
=_____;
=_____.
2
3
4
5
6
7
观察两者有什么关系?
互动新授
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
发现:
两个二次根式相除, 不变, 相除.
根指数
被开方数
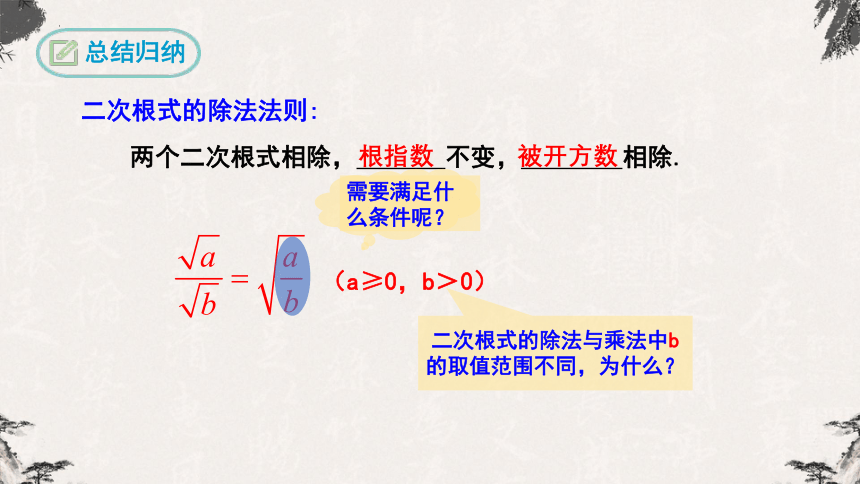
总结归纳
二次根式的除法法则:
两个二次根式相除, 不变, 相除.
根指数
被开方数
需要满足什么条件呢?
(a≥0,b>0)
二次根式的除法与乘法中b的取值范围不同,为什么?
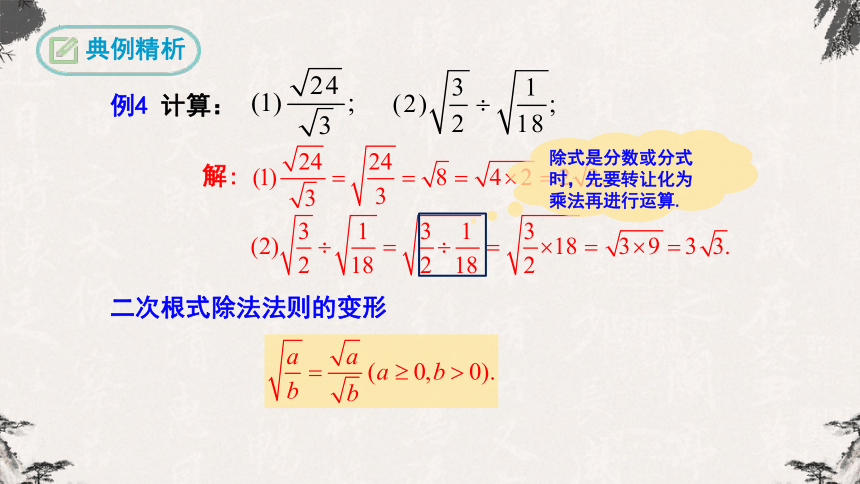
典例精析
例4 计算:
解:
除式是分数或分式时,先要转让化为乘法再进行运算.
二次根式除法法则的变形
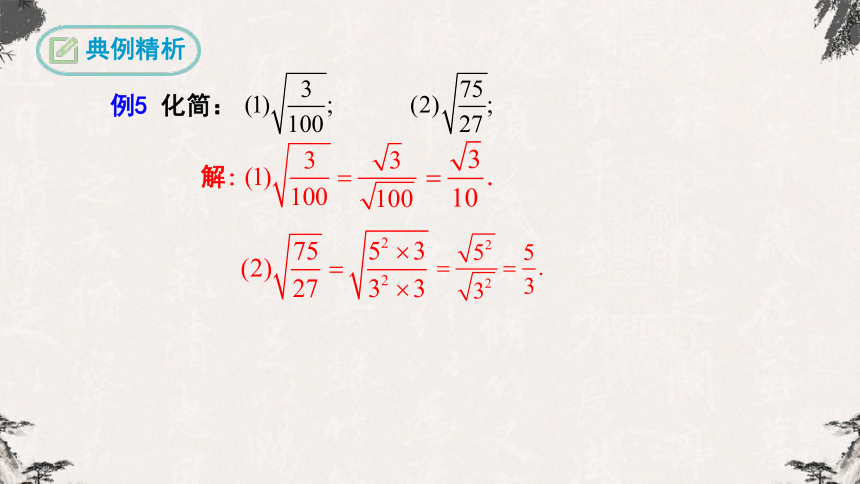
典例精析
例5 化简:
解:
在解法2中,式子变形
是为了去掉分母中的根号.
典例精析
例6 计算:
总结归纳
观察上面例4、例5、例6中各类小题的最后结果,比如 等,你发现有何特点?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
前面我们学习了二次根式的除法法则,你会去掉 这样的式子分母的根号吗?
是不是可以用分数的基本性质去掉分母的根号呢?
互动新授
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
典例精析
例7 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
解:∵
∴
小试牛刀
1.计算:
2.下列根式中,最简二次根式是( )
A. B. C. D.
1.化简 的结果是( )
A.9 B.3 C. D.
B
D
课堂检测
2. 化简:
解:
课堂检测
解:
1.化简:
拓展训练
二次根式除法
法则
性质
相关概念
最简二次根式
分母有理化
课堂小结
1.在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
课后作业
谢谢聆听
第16.2.2 二次根式的除法
人教版数学八年级下册
学习目标
1.了解二次根式的除法法则.
2.会运用除法法则及商的算术平方根进行简单运算.
3.能将二次根式化为最简二次根式.
计算下列各式,观察计算结果,你能发现什么规律?
合作探究
(1) ___÷___=____;
=_____;
(2) ___÷___=____;
(3) ___÷___=____;
=_____;
=_____.
2
3
4
5
6
7
观察两者有什么关系?
互动新授
观察三组式子的结果,我们得到下面三个等式:
(1)
(2)
(3)
发现:
两个二次根式相除, 不变, 相除.
根指数
被开方数
总结归纳
二次根式的除法法则:
两个二次根式相除, 不变, 相除.
根指数
被开方数
需要满足什么条件呢?
(a≥0,b>0)
二次根式的除法与乘法中b的取值范围不同,为什么?
典例精析
例4 计算:
解:
除式是分数或分式时,先要转让化为乘法再进行运算.
二次根式除法法则的变形
典例精析
例5 化简:
解:
在解法2中,式子变形
是为了去掉分母中的根号.
典例精析
例6 计算:
总结归纳
观察上面例4、例5、例6中各类小题的最后结果,比如 等,你发现有何特点?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
在二次根式的运算中,一般要把最后结果化为最简二次根式,并且分母中不含二次根式.
前面我们学习了二次根式的除法法则,你会去掉 这样的式子分母的根号吗?
是不是可以用分数的基本性质去掉分母的根号呢?
互动新授
把分母中的根号化去,使分母变成有理数的这个过程就叫做分母有理化.
典例精析
例7 设长方形的面积为S,相邻两边长分别为a,b.已知 ,求a的值.
解:∵
∴
小试牛刀
1.计算:
2.下列根式中,最简二次根式是( )
A. B. C. D.
1.化简 的结果是( )
A.9 B.3 C. D.
B
D
课堂检测
2. 化简:
解:
课堂检测
解:
1.化简:
拓展训练
二次根式除法
法则
性质
相关概念
最简二次根式
分母有理化
课堂小结
1.在下列各式中,哪些是最简二次根式?哪些不是?对不是最简二次根式的进行化简.
解:只有(3)是最简二次根式;
课后作业
谢谢聆听
