北师大版2022-2023学年七年级数学上册5.5 应用一元一次方程-“希望工程义演” 教学课件(共28张PPT)
文档属性
| 名称 | 北师大版2022-2023学年七年级数学上册5.5 应用一元一次方程-“希望工程义演” 教学课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 618.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-13 21:00:01 | ||
图片预览








文档简介
(共27张PPT)
第五章 一元一次方程
5.5 应用一元一次方程—“希望工程义演”
北师大版七年级上册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、利用表格中的数据分析问题中的数量关系,并且设出未知数,用未知数去表示其他的量;
2、正确根据题目中所给条件,找出等量关系,列出方程解决实际问题;
希望工程是由团中央、中国青少年发展基金会于1989年发起的以救助贫困地区失学少年儿童为目的的一项公益事业。其宗旨是建设希望小学,资助贫困地区失学儿童重返校园,改善农村办学条件。
讲授新课
知识点一 用一元一次方程解决数量分配问题
合作探究
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款69500元,成人票与学生票各售出多少张?
成人票 80元
学生票 50元
成人票数+________=1000张;
________+学生票款=________.
分析题意可得此题中的等量关系有:
学生票数
成人票款
69500元
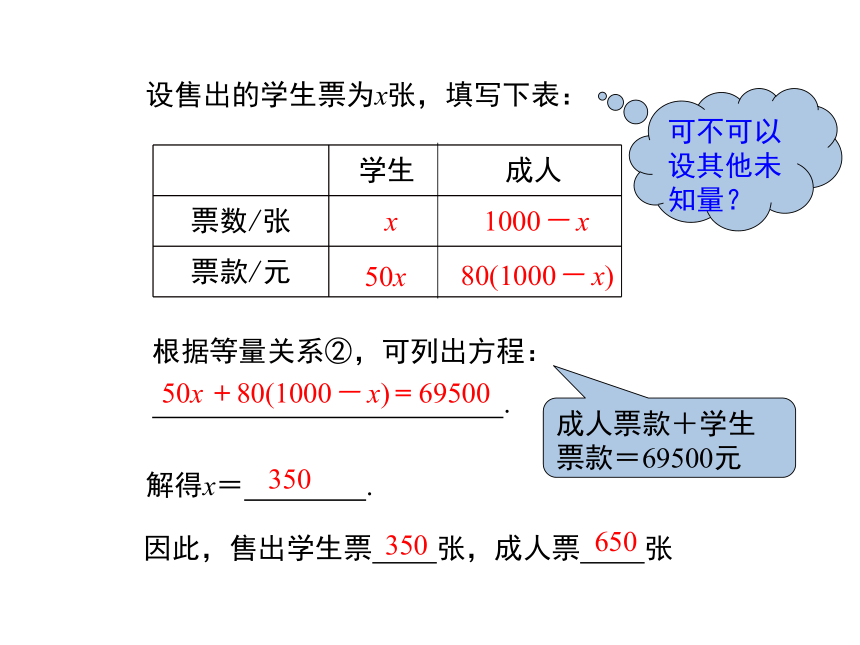
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
根据等量关系②,可列出方程:
.
解得x= .
因此,售出学生票 张,成人票 张
x
1000- x
50x
80(1000- x)
成人票款+学生票款=69500元
50x
80(1000- x)
+ = 69500
350
350
650
可不可以设其他未知量?
设所得的学生票款为y元,填写下表:
学生 成人
票数/张
票款/元
根据等量关系②,可列出方程:
.
解得y= .
因此,售出成人票 张,学生票 张
y/50
(69500- y)/80
y
69500- y
y/50
(69500- y)/80
+ = 1000
17500
650
350
方法总结:
1.当遇到的问题较复杂,含有两个未知量、两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量就用其中的一个等量关系表示为含未知数的代数式,而另一个等量关系则用来列方程.
2.可以采用列表格的方法搞清较复杂问题中的各个量之间的关系.
3.选择恰当的设未知数的方法.
议一议
如果票价不变,那么售出1000张票所得票款可能是69300元吗?为什么?
解:设售出的学生票为x张,则成人票为(1000-x)张,根据题意,得
50x+80(1000-x)=69300.
票的张数不可能是分数,所以不可能.
做一做
将这个问题中的“共售1000张票”改为“成人票比学生票多300张”,成人票和学生票各售出多少张?该如何解决?
解:设售出的学生票为x张,则成人票为(x+300)张,由题意,得
50x+80(x+300)=69500.
解得x=350,350+300=650.
答:售出学生票350张,成人票650张.
典例精析
例1 某地为了打造风光带,将一段长为360 m的河道整治任务交给甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24 m,乙工程队每天整治16 m,求甲、乙两个工程队分别整治了多长的河道.
[解析]等量关系:
甲工程队用时+乙工程队用时=20天,
甲工程队完成长度+乙工程队完成长度=360米.
解:设甲工程队整治了x米的河道,则乙工程队整治了(360-x)米的河道,根据题意,得
答:甲工程队整治了120米的河道,乙工程队整治了240米的河道.
解得x=120.
所以360-x=240.
当堂练习
1.我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐.问人数和车数各是多少?设车x辆,根据题意,可列出的方程是( )
A.3(x-2)=2x+9 B.3(x-2)=2(x+9)
C.3x-2=2x+9 D.3x-2=2(x+9)
【答案】A
【分析】本题两种乘车方式中,车的数量与人的数量都是相等的,可以将车的数量设为x辆,根据人数相等列出方程即可.
【详解】解:设车有x辆,
若每车坐三人,则人数为3(x-2)人
若每车坐两人,则人数为(2x+9)人
故3(x-2)=(2x+9)
故选A
2.商店将标价为6元的笔记本,采用如下方式进行促销;若购买不超过3本,则按原价付款;若一次性购买3本以上,则超过的部分打七折.小明有54元钱,他购买笔记本的数量是( )
A.11本 B.最少11本 C.最多11本 D.最多12本
【答案】C
【分析】易得54元可购买的商品一定超过了3本,关系式为:3×原价+超过3本的本数×打折后的价格≤54,把相关数值代入计算求得最大的正整数解即可.
3.某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;若每人做4个,则将比计划少做15个,现有下列四个方程:①5m+9=4m-15;②;③=;④5m-9=4m+15.其中正确的是( )
A.①② B.②④ C.②③ D.③④
【详解】解:由某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;
可得:中国结的数量为:(5m-9)个,
若每人做4个,则将比计划少做15个,
可得:中国结的数量为:(4m+15)个,
∴5m-9=4m+15,故④符合题意,①不符合题意;
由某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;
可得:某小组有人,
若每人做4个,则将比计划少做15个,
可得:某小组有人,
∴=故②不符合题意,③符合题意;
故选:D.
4.甲、乙两店以同样价格出售一种商品,并推出不同的优惠方案在甲店累计购物超过100元后,超出100元的部分打9折;在乙店累计购物超过50元后,超出50元的部分打9.5折,则顾客到两店购物花费一样时为( )
A.累计购物不超过50元 B.累计购物超过50元不超过100元
C.累计购物超过100元 D.累计购物不超过50元或刚好为150元
【答案】D
【分析】设顾客累计购物x元时,两店花费一样多,分x>100及x≤50两种情况考虑,当x≤50时,显然两店花费一样多;当x>100时,根据优惠方案列出关于x的一元一次方程,解之即可得出结论.
5.某校初中一年级组织学生春游活动,如果包车6辆会有10个学生没有座位,如果包车7辆则会多出30个空位,则该年级学生人数为______人.
【答案】250
【详解】解:设1辆包车有x个座位,依题意有
6x+10=7x-30
解得x=40,
6x+10=6×40+10=250.
故该年级学生人数为250人.
故答案为:250.
6.把一些图书分给某组学生阅读,如果每人分4本,则剩余1本;如果每人分5本,则还缺4本,这个小组的学生有____人.
【答案】5
【分析】设这个班有x名学生,根据“如果每人分4本,则剩余1本;如果每人分5本,则还缺4本”建立方程求解即可.
【详解】解:设这个小组的学生有x本
4x+1=5x-4
x=5
故答案为:5.
7.某车间有66名工人,每名工人一天能生产甲种零件24个或生产乙种零件15个,而甲种零件3个,乙种零件5个配成一套机件,请合理分配所有工人,使得每天生产的零件刚好配低,则每天可生产_____套.
【答案】144
【分析】设应分配x人生产甲种零件,则(66-x)人生产乙种零件,才能使每天生产的这两种零件配套.根据每人每天平均能生产甲种零件24个或乙种零件15个,可列方程求解.
8.某商场在“十一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:
①如果不超过500元,则不予优惠;
②如果超过500元,但不超过800元,则按购物总额给予8折优惠;
③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.
促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和m(500<m≤640)元;若合并付款,则她们总共只需付款___________元.(请用含m的代数式表示)
【答案】()或(+520)
【分析】根据题意知付款480元,其实际标价为480元或600元,付款m元,其实际标价为元,分两种情况分别计算出合并购买总标价(480+)元或(600+)元的商品应付款即可.
【点睛】本题考查的是列代数式,寻找题中数量关系是解题关键.
9.在国庆放假期间,某校长带领该校部分学生去北京旅游.甲旅行社说∶“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说∶“包括校长在内的全部按全票价的6折优惠.”现已知全票价为240元.
(1)设学生人数为x,甲旅行社收费为y甲,乙旅行社收费为y乙,分别计算两家旅行社的收费.
(2)当学生人数为多少时,两家旅行社的收费一样?
【详解】(1)解:y甲=240+240×50%×x=120x+240,
y乙=(x+1)×240×60%=(x+1)×144=144x+144,
答:甲旅行社收费为(120x+240)元,乙旅行社收费为(144x+144)元;
(2)解:当两家旅行社收费一样时∶
240+120x=144+144x
144x-120x=240-144
24x=96
x=4
答∶当学生是4人时,两家旅行社的收费一样.
10.为贯彻落实“双减”政策,积极开拓校本研修课程,某校课外实践小组欲到植物园开展研修活动,植物园提供以下三种购票方式:
购买散票:每人一张20元;
当购票人数不小于100人时,可以选择购买优惠票或团队票;
购买优惠票:可以享受票价9折优惠;
购买团队票:一张团队票2400元,且入园时,每人还需付10元.
(1)若有100名学生到植物园开展研修活动,你认为如何购票优惠?请计算说明;
(2)当入园人数达到多少时,购买优惠票与购买团体票的价钱相同?
【详解】(1)解:购买散票:100×20=2000元;
购买优惠票:100×20×90%=1800元;
购买团队票:2400+100×1=03400元;
∵1800<2000<3400
∴购买优惠票优惠;
(2)解:设入园人数达到x(x≥100)人时,购买优惠票与购买团体票的价钱相同,
∴20×90%x=2400+10x
解得,x=300(人),
答:当入园人数达到300人时,购买优惠票与购买团体票的价钱相同.
课堂小结
应用一元一次方程解决实际问题的一般步骤.
第五章 一元一次方程
5.5 应用一元一次方程—“希望工程义演”
北师大版七年级上册
新课导入
讲授新课
当堂检测
课堂小结
学习目标
1、利用表格中的数据分析问题中的数量关系,并且设出未知数,用未知数去表示其他的量;
2、正确根据题目中所给条件,找出等量关系,列出方程解决实际问题;
希望工程是由团中央、中国青少年发展基金会于1989年发起的以救助贫困地区失学少年儿童为目的的一项公益事业。其宗旨是建设希望小学,资助贫困地区失学儿童重返校园,改善农村办学条件。
讲授新课
知识点一 用一元一次方程解决数量分配问题
合作探究
某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹得票款69500元,成人票与学生票各售出多少张?
成人票 80元
学生票 50元
成人票数+________=1000张;
________+学生票款=________.
分析题意可得此题中的等量关系有:
学生票数
成人票款
69500元
设售出的学生票为x张,填写下表:
学生 成人
票数/张
票款/元
根据等量关系②,可列出方程:
.
解得x= .
因此,售出学生票 张,成人票 张
x
1000- x
50x
80(1000- x)
成人票款+学生票款=69500元
50x
80(1000- x)
+ = 69500
350
350
650
可不可以设其他未知量?
设所得的学生票款为y元,填写下表:
学生 成人
票数/张
票款/元
根据等量关系②,可列出方程:
.
解得y= .
因此,售出成人票 张,学生票 张
y/50
(69500- y)/80
y
69500- y
y/50
(69500- y)/80
+ = 1000
17500
650
350
方法总结:
1.当遇到的问题较复杂,含有两个未知量、两个等量关系时,可以把其中一个未知量设为未知数,另一个未知量就用其中的一个等量关系表示为含未知数的代数式,而另一个等量关系则用来列方程.
2.可以采用列表格的方法搞清较复杂问题中的各个量之间的关系.
3.选择恰当的设未知数的方法.
议一议
如果票价不变,那么售出1000张票所得票款可能是69300元吗?为什么?
解:设售出的学生票为x张,则成人票为(1000-x)张,根据题意,得
50x+80(1000-x)=69300.
票的张数不可能是分数,所以不可能.
做一做
将这个问题中的“共售1000张票”改为“成人票比学生票多300张”,成人票和学生票各售出多少张?该如何解决?
解:设售出的学生票为x张,则成人票为(x+300)张,由题意,得
50x+80(x+300)=69500.
解得x=350,350+300=650.
答:售出学生票350张,成人票650张.
典例精析
例1 某地为了打造风光带,将一段长为360 m的河道整治任务交给甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24 m,乙工程队每天整治16 m,求甲、乙两个工程队分别整治了多长的河道.
[解析]等量关系:
甲工程队用时+乙工程队用时=20天,
甲工程队完成长度+乙工程队完成长度=360米.
解:设甲工程队整治了x米的河道,则乙工程队整治了(360-x)米的河道,根据题意,得
答:甲工程队整治了120米的河道,乙工程队整治了240米的河道.
解得x=120.
所以360-x=240.
当堂练习
1.我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,两车空出来;每车坐2人,多出9人无车坐.问人数和车数各是多少?设车x辆,根据题意,可列出的方程是( )
A.3(x-2)=2x+9 B.3(x-2)=2(x+9)
C.3x-2=2x+9 D.3x-2=2(x+9)
【答案】A
【分析】本题两种乘车方式中,车的数量与人的数量都是相等的,可以将车的数量设为x辆,根据人数相等列出方程即可.
【详解】解:设车有x辆,
若每车坐三人,则人数为3(x-2)人
若每车坐两人,则人数为(2x+9)人
故3(x-2)=(2x+9)
故选A
2.商店将标价为6元的笔记本,采用如下方式进行促销;若购买不超过3本,则按原价付款;若一次性购买3本以上,则超过的部分打七折.小明有54元钱,他购买笔记本的数量是( )
A.11本 B.最少11本 C.最多11本 D.最多12本
【答案】C
【分析】易得54元可购买的商品一定超过了3本,关系式为:3×原价+超过3本的本数×打折后的价格≤54,把相关数值代入计算求得最大的正整数解即可.
3.某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;若每人做4个,则将比计划少做15个,现有下列四个方程:①5m+9=4m-15;②;③=;④5m-9=4m+15.其中正确的是( )
A.①② B.②④ C.②③ D.③④
【详解】解:由某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;
可得:中国结的数量为:(5m-9)个,
若每人做4个,则将比计划少做15个,
可得:中国结的数量为:(4m+15)个,
∴5m-9=4m+15,故④符合题意,①不符合题意;
由某小组有m人,计划做n个“中国结”,若每人做5个,则可比计划多做9个;
可得:某小组有人,
若每人做4个,则将比计划少做15个,
可得:某小组有人,
∴=故②不符合题意,③符合题意;
故选:D.
4.甲、乙两店以同样价格出售一种商品,并推出不同的优惠方案在甲店累计购物超过100元后,超出100元的部分打9折;在乙店累计购物超过50元后,超出50元的部分打9.5折,则顾客到两店购物花费一样时为( )
A.累计购物不超过50元 B.累计购物超过50元不超过100元
C.累计购物超过100元 D.累计购物不超过50元或刚好为150元
【答案】D
【分析】设顾客累计购物x元时,两店花费一样多,分x>100及x≤50两种情况考虑,当x≤50时,显然两店花费一样多;当x>100时,根据优惠方案列出关于x的一元一次方程,解之即可得出结论.
5.某校初中一年级组织学生春游活动,如果包车6辆会有10个学生没有座位,如果包车7辆则会多出30个空位,则该年级学生人数为______人.
【答案】250
【详解】解:设1辆包车有x个座位,依题意有
6x+10=7x-30
解得x=40,
6x+10=6×40+10=250.
故该年级学生人数为250人.
故答案为:250.
6.把一些图书分给某组学生阅读,如果每人分4本,则剩余1本;如果每人分5本,则还缺4本,这个小组的学生有____人.
【答案】5
【分析】设这个班有x名学生,根据“如果每人分4本,则剩余1本;如果每人分5本,则还缺4本”建立方程求解即可.
【详解】解:设这个小组的学生有x本
4x+1=5x-4
x=5
故答案为:5.
7.某车间有66名工人,每名工人一天能生产甲种零件24个或生产乙种零件15个,而甲种零件3个,乙种零件5个配成一套机件,请合理分配所有工人,使得每天生产的零件刚好配低,则每天可生产_____套.
【答案】144
【分析】设应分配x人生产甲种零件,则(66-x)人生产乙种零件,才能使每天生产的这两种零件配套.根据每人每天平均能生产甲种零件24个或乙种零件15个,可列方程求解.
8.某商场在“十一”期间举行促销活动,根据顾客按商品标价一次性购物总额,规定相应的优惠方法:
①如果不超过500元,则不予优惠;
②如果超过500元,但不超过800元,则按购物总额给予8折优惠;
③如果超过800元,则其中800元给予8折优惠,超过800元的部分给予6折优惠.
促销期间,小红和她母亲分别看中一件商品,若各自单独付款,则应分别付款480元和m(500<m≤640)元;若合并付款,则她们总共只需付款___________元.(请用含m的代数式表示)
【答案】()或(+520)
【分析】根据题意知付款480元,其实际标价为480元或600元,付款m元,其实际标价为元,分两种情况分别计算出合并购买总标价(480+)元或(600+)元的商品应付款即可.
【点睛】本题考查的是列代数式,寻找题中数量关系是解题关键.
9.在国庆放假期间,某校长带领该校部分学生去北京旅游.甲旅行社说∶“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说∶“包括校长在内的全部按全票价的6折优惠.”现已知全票价为240元.
(1)设学生人数为x,甲旅行社收费为y甲,乙旅行社收费为y乙,分别计算两家旅行社的收费.
(2)当学生人数为多少时,两家旅行社的收费一样?
【详解】(1)解:y甲=240+240×50%×x=120x+240,
y乙=(x+1)×240×60%=(x+1)×144=144x+144,
答:甲旅行社收费为(120x+240)元,乙旅行社收费为(144x+144)元;
(2)解:当两家旅行社收费一样时∶
240+120x=144+144x
144x-120x=240-144
24x=96
x=4
答∶当学生是4人时,两家旅行社的收费一样.
10.为贯彻落实“双减”政策,积极开拓校本研修课程,某校课外实践小组欲到植物园开展研修活动,植物园提供以下三种购票方式:
购买散票:每人一张20元;
当购票人数不小于100人时,可以选择购买优惠票或团队票;
购买优惠票:可以享受票价9折优惠;
购买团队票:一张团队票2400元,且入园时,每人还需付10元.
(1)若有100名学生到植物园开展研修活动,你认为如何购票优惠?请计算说明;
(2)当入园人数达到多少时,购买优惠票与购买团体票的价钱相同?
【详解】(1)解:购买散票:100×20=2000元;
购买优惠票:100×20×90%=1800元;
购买团队票:2400+100×1=03400元;
∵1800<2000<3400
∴购买优惠票优惠;
(2)解:设入园人数达到x(x≥100)人时,购买优惠票与购买团体票的价钱相同,
∴20×90%x=2400+10x
解得,x=300(人),
答:当入园人数达到300人时,购买优惠票与购买团体票的价钱相同.
课堂小结
应用一元一次方程解决实际问题的一般步骤.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
