2022-2023学年高一上学期数学北师大版(2019)必修第一册8.2数学建模的主要步骤 课件(共27张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学北师大版(2019)必修第一册8.2数学建模的主要步骤 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 21:42:22 | ||
图片预览








文档简介
(共27张PPT)
8 数学建模活动(一)
8.2 数学建模的主要步骤
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
提出问题
分析问题相关因素
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
这个问题涉及车长、车距、车速、堵塞的干扰等多种因素.而不同型号车的车长是不同的,驾驶员的习惯不同也会使车距、车速不同,行人和非机动车的干扰因素则复杂且不确定,面对这些不同和不确定,就需要进行梳理和筛选.
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
思考影响因素:
1、车型不一样怎么处理?
2、等待绿灯时各个汽车的位置有什么特点?
3、按车头算距离还是车尾计算距离?
4、绿灯亮前后,汽车运动状态发生了什么变化?
5、绿灯亮后,司机会做出什么反应?
6、道路畅通状态如何?
筛选问题相关因素
(1)通过路口的车辆长度都相等;
(2)等待时,前后相邻两辆车的车距都相等;
(3)绿灯亮后,汽车都是在静止状态下匀加速启动;
(4)前一辆车启动后,下一辆车启动的延时时间相等;
(5)车辆行驶秩序良好,不会发生堵塞.
针对相关因素作出假设
这是建模的重要环节——假设
确立参数
车辆长度记作 , =5m
车距记作d,d=2m
汽车加速启动,加速度记作a,a=2
城市十字路口限速记作v*,v*=40km/h≈11.1m/s
延时时间记作T,T=1s
第n辆汽车开始启动的时间记作 ,则
第n辆车到达最高限速的时间记作
则汽车做匀加速运动的时间是
第n辆汽车在时刻t时所在的位置记作
停车线位置记作0,
建立模型
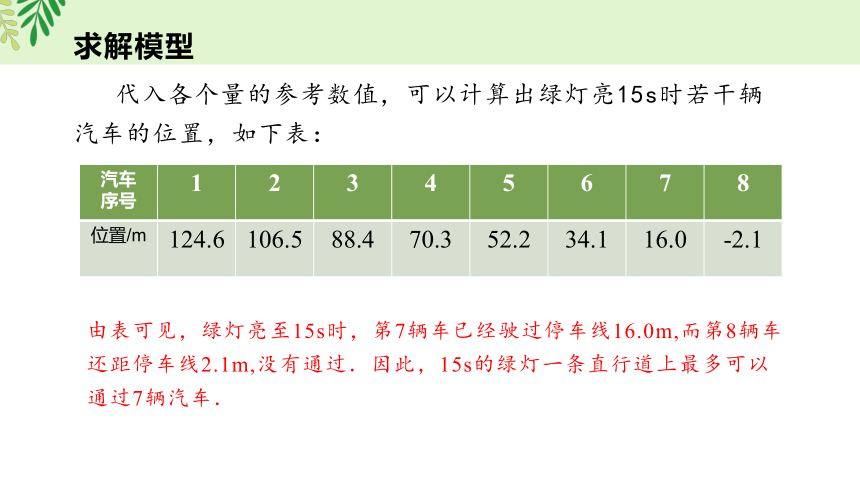
汽车 序号 1 2 3 4 5 6 7 8
位置/m 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
代入各个量的参考数值,可以计算出绿灯亮15s时若干辆汽车的位置,如下表:
由表可见,绿灯亮至15s时,第7辆车已经驶过停车线16.0m,而第8辆车还距停车线2.1m,没有通过.因此,15s的绿灯一条直行道上最多可以通过7辆汽车.
求解模型
课后,请同学们到十字路口实地调查,对结论做检验.若没有明显误差,就可以使用这个模型.否则,再修改假设,重新建模.
检验结果
思考交流
1.从小学到中学,在数学学习中,做过不少“应用题”,比较上述实际问题的解决,说明用数学建模的方法解决实际问题和做应用题有什么联系和区别.
2.总结数学建模的基本步骤.
做数学建模与做应用题的联系与区别
二者的联系:目的都是运用数学解决实际问题,都体现了从实际问题转化为数学问题并进行解决的过程,从局部的步骤上看也有相似之处.
二者的区别是:(1)问题的特征:应用题中的问题比较明确,涉及的数据和信息大多是经过数学专家和命题者加工提炼后,以文字或图的形式给出;条件清楚准确、不多不少,结论唯一确定.数学建模所面对的问题来源则更生活化,更贴近实际;条件和结论更模糊,数据一般需要同学们收集、挑选、整理后才能进一步运用.
(2)解决过程:应用题问题数学化的过程简单、清楚明了,解出的结论很少需要我们思考是否合乎实际、是否需要进一步调整和修改已有的模型.数学建模一般不会有现成的数据、陈述、关系等条件,需要同学们明确提出问题,对条件进行合理假设、数学化以及检验结果.
合乎实际
实际情境
提出问题
建立模型
求解模型
实际结果
检验结果
不合乎实际
数学建模一般步骤
合作探究
中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85 ℃的水泡制,再等到茶水温度降至60 ℃时饮用,可以产生最佳口感.那么在25 ℃室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感?
探究:1、解决这个问题需要搜集哪些数据?
2、可以利用哪些工具?
3、怎样排除干扰因素?
课堂小结
合乎实际
实际情境
提出问题
建立模型
求解模型
实际结果
检验结果
不合乎实际
数学建模一般步骤
课后作业
1、选择你熟悉的路口,具体调查它的通行能力(如待转线的车流量是多少?左转灯的绿灯设置多长时间合理?),采用本节的方法尝试数学建模.
2、在互联网上搜索一篇数学建模论文,并分析步骤,审视假设的合理性.
3、应在炒菜之前多长时间将冰箱里的肉拿出来解冻?请大家课后分小组合作探究.
教学阐释
目录
CONTENTS
教材解读
01
学情分析
02
目标定位
03
教学重难点
04
课程设计
05
教学评价
06
教材解读
必修第一册
选择性必修第一册
必修第二册
必修第一册
必修第二册
选择性必修第一册
本节课的主要内容是讲解数学建模的一般步骤.从一个生活中的实例“十字路口汽车问题”出发,说明了数学建模的四个步骤:提出问题-建立模型-求解模型-检验结果.由此让学生认识数学建模,并进一步理解数学建模的意义.教材突出了建立模型的过程,详细地展示了建模的重要环节-模型假设的过程.这是学生不熟悉的,也是十分重要的.从原始问题很难迅速得出数学模型,需要作相关因素的分析、假设、抽象的数学加工,进而选择适当的数学方法和模型,根据模型的需要开展有针对性的数据调查工作和数据整理工作.
学情分析
数学建模的主要步骤有着较丰富的内容.比如,“提出问题”怎么实现?很多学生找不到问题,这就需要教师引导学生发现问题,还能将问题表达清楚.另外,“建立模型”先要分析问题的相关因素,做合理的假设,这些都是不容易做到的,并且是学生比较陌生的,不能把建模步骤看得太简单了.就本章而言,课程要求只提到“了解”.
但我们仍然要尝试进行数学建模的实践.因为数学建模要在“做中学”,这仍然是教学的重点,只不过是“初步实践”.
目标定位
1.通过“十字路口汽车问题”的学习,了解数学建模的一般步骤.
2.理解做数学建模与做应用题的联系与区别,进一步理解数学建模的意义.
3.通过亲身参与实践活动,增强发现问题的意识,提高提出问题,分析、解决问题和构建模型的能力,提升数学建模核心素养.
教学重难点
重点:掌握数学建模的基本步骤,理解“数学建模”与“应用题”的区别.
难点:理解“建立模型”的过程.
对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题
提出问题
分析问题相关因素
筛选问题相关因素作出假设、确立参数、构建模型
建立模型
学生分工合作
求解数学问题
求解模型
实际场景调查,检验结果是否符合实际,如果不符合实际,改进或者重新建模.
检验结果
课程设计
走进数学建模
1.本节课结合实例把握数学建模的一般步骤.重点是让学生明确数学建模的整体过程,明确每一步的作用是什么,每一步具体做什么,“检验结果”如何进行.这是学生做数学建模的前提.让学生亲身实践,探讨合作,增强问题意识,提升数学建模素养.
2.详细分析“建立模型”这个重要步骤.“建立模型”其实要做四件事:第一件事是分析与问题相关的因素;第二件事是对各个相关因素作出假设,呈现从实际问题中筛选出来的条件;第三件事是选择适当的数学模型表达实际问题;第四件事是针对模型的参数进行调查研究,收集数据.这几件事是有顺序的,在本节课的实例中都有体现,只不过没有真正让学生去收集数据,而是根据教学的需要以“另据调查”给了出来,并向学生讲清楚,数据实际上应当是做建模的人自己去收集的.
3.重视澄清做应用题与做数学建模的区别,让学生进一步理解数学建模的意义.
教学评价
感谢观看
8 数学建模活动(一)
8.2 数学建模的主要步骤
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
提出问题
分析问题相关因素
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
这个问题涉及车长、车距、车速、堵塞的干扰等多种因素.而不同型号车的车长是不同的,驾驶员的习惯不同也会使车距、车速不同,行人和非机动车的干扰因素则复杂且不确定,面对这些不同和不确定,就需要进行梳理和筛选.
在一个十字路口,每次亮绿灯的时长为15s,那么,每次绿灯亮时,在一条直行道路上能有多少汽车通过十字路口?
思考影响因素:
1、车型不一样怎么处理?
2、等待绿灯时各个汽车的位置有什么特点?
3、按车头算距离还是车尾计算距离?
4、绿灯亮前后,汽车运动状态发生了什么变化?
5、绿灯亮后,司机会做出什么反应?
6、道路畅通状态如何?
筛选问题相关因素
(1)通过路口的车辆长度都相等;
(2)等待时,前后相邻两辆车的车距都相等;
(3)绿灯亮后,汽车都是在静止状态下匀加速启动;
(4)前一辆车启动后,下一辆车启动的延时时间相等;
(5)车辆行驶秩序良好,不会发生堵塞.
针对相关因素作出假设
这是建模的重要环节——假设
确立参数
车辆长度记作 , =5m
车距记作d,d=2m
汽车加速启动,加速度记作a,a=2
城市十字路口限速记作v*,v*=40km/h≈11.1m/s
延时时间记作T,T=1s
第n辆汽车开始启动的时间记作 ,则
第n辆车到达最高限速的时间记作
则汽车做匀加速运动的时间是
第n辆汽车在时刻t时所在的位置记作
停车线位置记作0,
建立模型
汽车 序号 1 2 3 4 5 6 7 8
位置/m 124.6 106.5 88.4 70.3 52.2 34.1 16.0 -2.1
代入各个量的参考数值,可以计算出绿灯亮15s时若干辆汽车的位置,如下表:
由表可见,绿灯亮至15s时,第7辆车已经驶过停车线16.0m,而第8辆车还距停车线2.1m,没有通过.因此,15s的绿灯一条直行道上最多可以通过7辆汽车.
求解模型
课后,请同学们到十字路口实地调查,对结论做检验.若没有明显误差,就可以使用这个模型.否则,再修改假设,重新建模.
检验结果
思考交流
1.从小学到中学,在数学学习中,做过不少“应用题”,比较上述实际问题的解决,说明用数学建模的方法解决实际问题和做应用题有什么联系和区别.
2.总结数学建模的基本步骤.
做数学建模与做应用题的联系与区别
二者的联系:目的都是运用数学解决实际问题,都体现了从实际问题转化为数学问题并进行解决的过程,从局部的步骤上看也有相似之处.
二者的区别是:(1)问题的特征:应用题中的问题比较明确,涉及的数据和信息大多是经过数学专家和命题者加工提炼后,以文字或图的形式给出;条件清楚准确、不多不少,结论唯一确定.数学建模所面对的问题来源则更生活化,更贴近实际;条件和结论更模糊,数据一般需要同学们收集、挑选、整理后才能进一步运用.
(2)解决过程:应用题问题数学化的过程简单、清楚明了,解出的结论很少需要我们思考是否合乎实际、是否需要进一步调整和修改已有的模型.数学建模一般不会有现成的数据、陈述、关系等条件,需要同学们明确提出问题,对条件进行合理假设、数学化以及检验结果.
合乎实际
实际情境
提出问题
建立模型
求解模型
实际结果
检验结果
不合乎实际
数学建模一般步骤
合作探究
中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85 ℃的水泡制,再等到茶水温度降至60 ℃时饮用,可以产生最佳口感.那么在25 ℃室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感?
探究:1、解决这个问题需要搜集哪些数据?
2、可以利用哪些工具?
3、怎样排除干扰因素?
课堂小结
合乎实际
实际情境
提出问题
建立模型
求解模型
实际结果
检验结果
不合乎实际
数学建模一般步骤
课后作业
1、选择你熟悉的路口,具体调查它的通行能力(如待转线的车流量是多少?左转灯的绿灯设置多长时间合理?),采用本节的方法尝试数学建模.
2、在互联网上搜索一篇数学建模论文,并分析步骤,审视假设的合理性.
3、应在炒菜之前多长时间将冰箱里的肉拿出来解冻?请大家课后分小组合作探究.
教学阐释
目录
CONTENTS
教材解读
01
学情分析
02
目标定位
03
教学重难点
04
课程设计
05
教学评价
06
教材解读
必修第一册
选择性必修第一册
必修第二册
必修第一册
必修第二册
选择性必修第一册
本节课的主要内容是讲解数学建模的一般步骤.从一个生活中的实例“十字路口汽车问题”出发,说明了数学建模的四个步骤:提出问题-建立模型-求解模型-检验结果.由此让学生认识数学建模,并进一步理解数学建模的意义.教材突出了建立模型的过程,详细地展示了建模的重要环节-模型假设的过程.这是学生不熟悉的,也是十分重要的.从原始问题很难迅速得出数学模型,需要作相关因素的分析、假设、抽象的数学加工,进而选择适当的数学方法和模型,根据模型的需要开展有针对性的数据调查工作和数据整理工作.
学情分析
数学建模的主要步骤有着较丰富的内容.比如,“提出问题”怎么实现?很多学生找不到问题,这就需要教师引导学生发现问题,还能将问题表达清楚.另外,“建立模型”先要分析问题的相关因素,做合理的假设,这些都是不容易做到的,并且是学生比较陌生的,不能把建模步骤看得太简单了.就本章而言,课程要求只提到“了解”.
但我们仍然要尝试进行数学建模的实践.因为数学建模要在“做中学”,这仍然是教学的重点,只不过是“初步实践”.
目标定位
1.通过“十字路口汽车问题”的学习,了解数学建模的一般步骤.
2.理解做数学建模与做应用题的联系与区别,进一步理解数学建模的意义.
3.通过亲身参与实践活动,增强发现问题的意识,提高提出问题,分析、解决问题和构建模型的能力,提升数学建模核心素养.
教学重难点
重点:掌握数学建模的基本步骤,理解“数学建模”与“应用题”的区别.
难点:理解“建立模型”的过程.
对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题
提出问题
分析问题相关因素
筛选问题相关因素作出假设、确立参数、构建模型
建立模型
学生分工合作
求解数学问题
求解模型
实际场景调查,检验结果是否符合实际,如果不符合实际,改进或者重新建模.
检验结果
课程设计
走进数学建模
1.本节课结合实例把握数学建模的一般步骤.重点是让学生明确数学建模的整体过程,明确每一步的作用是什么,每一步具体做什么,“检验结果”如何进行.这是学生做数学建模的前提.让学生亲身实践,探讨合作,增强问题意识,提升数学建模素养.
2.详细分析“建立模型”这个重要步骤.“建立模型”其实要做四件事:第一件事是分析与问题相关的因素;第二件事是对各个相关因素作出假设,呈现从实际问题中筛选出来的条件;第三件事是选择适当的数学模型表达实际问题;第四件事是针对模型的参数进行调查研究,收集数据.这几件事是有顺序的,在本节课的实例中都有体现,只不过没有真正让学生去收集数据,而是根据教学的需要以“另据调查”给了出来,并向学生讲清楚,数据实际上应当是做建模的人自己去收集的.
3.重视澄清做应用题与做数学建模的区别,让学生进一步理解数学建模的意义.
教学评价
感谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
