2022-2023学年高一上学期数学北师大版(2019)必修第一册8.1走近数学建模 课件(共22张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学北师大版(2019)必修第一册8.1走近数学建模 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
8.1 走近数学建模
陈琳娜
驻马店市第二高级中学
驻马店市第二高级中学
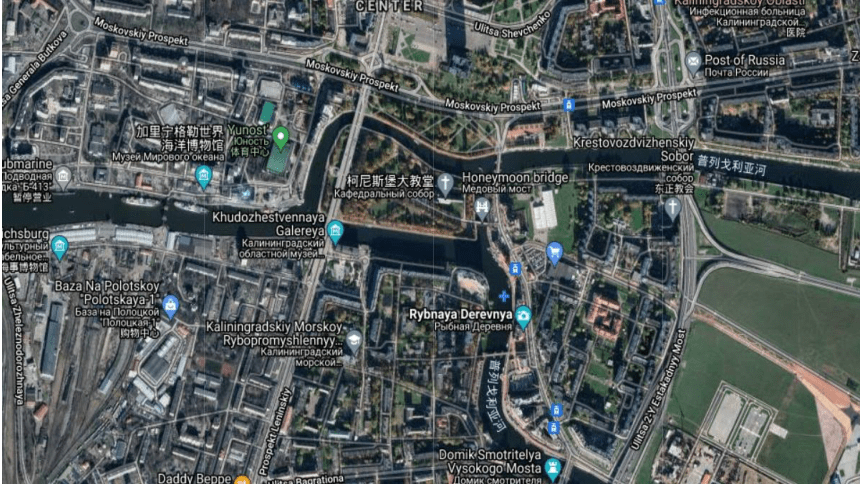
哥尼斯堡城
(今俄罗斯加里宁格勒)
康德
哥德巴赫
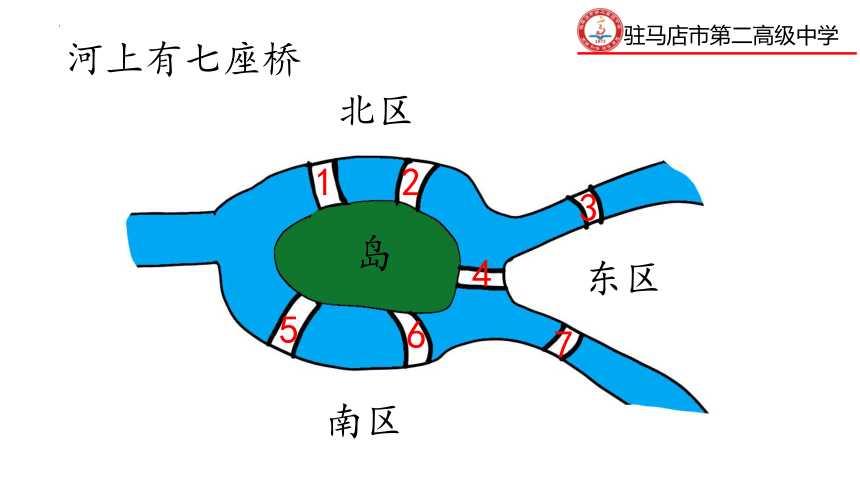
河上有七座桥
岛
北区
南区
东区
1
2
3
4
5
6
7
驻马店市第二高级中学
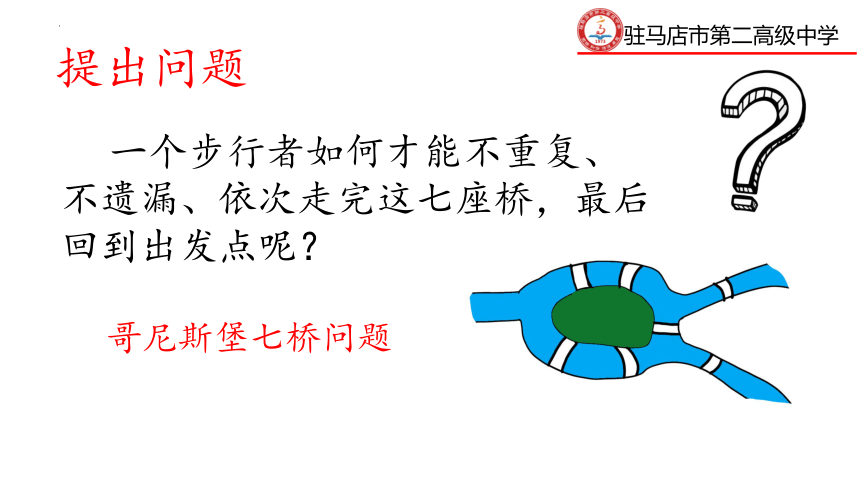
提出问题
一个步行者如何才能不重复、不遗漏、依次走完这七座桥,最后回到出发点呢?
哥尼斯堡七桥问题
驻马店市第二高级中学
莱昂哈德·欧拉(Leonhard Euler,1707年4月15日-1783年9月18日),瑞士数学家和物理学家,近代数学先驱之一。
驻马店市第二高级中学
数学抽象成排列组合问题
岛
北区
南区
东区
1
2
3
4
5
6
7
驻马店市第二高级中学
不同的走法
5040
种
驻马店市第二高级中学
实际问题的数学表述
1、岛的大小、形状影响结果吗?
2、桥的长短、宽窄影响结果吗?
不影响
不影响
驻马店市第二高级中学
陆地、桥与岛三者之间的位置关系影响结果
数学问题的解决
驻马店市第二高级中学
七桥问题数学模型
能否一笔画出此图形?
驻马店市第二高级中学
思考:“起点”、“终点”、“经过点”有什么特征?
偶点
偶点:以某一点为端点的线有偶数条
奇点:以某一点为端点的线有奇数条
驻马店市第二高级中学
一笔画定理(欧拉定理)
一个由点和线组成的图形能一笔画完,必须符合以下两个条件:
(1)图形是连在一起的,即是连通图形;
(2)图形中的奇点个数为0或2.
驻马店市第二高级中学
七桥问题中,四个点全是奇点,不能一笔画出,即不能一次无重复地走完七座桥。
用数学结论解答原问题
3
3
3
5
驻马店市第二高级中学
思考交流
1、实际问题是什么?
2、在转换成数学模型过程中,欧拉使用了哪些数学元素抽象地描述实际问题的元素?这种描述为什么不会对结果产生影响?
3、欧拉在求解模型的过程中研究出的“一笔画定理”是如何解决七桥问题的?
4、“一笔画定理”还可以用在哪些问题的解决中?
驻马店市第二高级中学
1、实际问题是:如何才能能一次无重复的走过哥尼斯堡城的七座桥,最后回到出发点。
2、在建立模型的过程中,欧拉用4个点表示被河隔开的4块陆地,用7条线表示连接陆地的七座桥,七桥问题就变成了由4个点和7条线组成的连通图形能否被一笔画出的问题,这种抽象对结果并不产生影响.起决定作用的仅是陆地、桥与岛这三者间的位置关系.
3、由一笔画定理可知连通图形中奇点个数为0个或2个。
七桥问题抽象出来的图形有4个奇点,不符合定理,不能一笔画出。
所以七座桥也不能一次不重复的走完。
4、一笔画问题在日常生活中有着广泛的应用.例如,快递员送快递怎样设计路线更省时?小区保安巡逻路线如何设计能提高效率?如何设计展厅最佳参观路线?
驻马店市第二高级中学
提出问题
建立模型
求解模型
检验结果
实际结果
数学建模
驻马店市第二高级中学
1、实际问题是:如何才能能一次无重复的走过哥尼斯堡城的七座桥,最后回到出发点。
2、在建立模型的过程中,欧拉用4个点表示被河隔开的4块陆地,用7条线表示连接陆地的七座桥,七桥问题就变成了由4个点和7条线组成的连通图形能否被一笔画出的问题,这种抽象对结果并不产生影响.起决定作用的仅是陆地、桥与岛这三者间的位置关系.
3、由一笔画定理可知连通图形中奇点个数为0个或2个。
七桥问题抽象出来的图形有4个奇点,不符合定理,不能一笔画出。
所以七座桥也不能一次不重复的走完。
4、一笔画问题在日常生活中有着广泛的应用.例如,快递员送快递怎样设计路线更省时?小区保安巡逻路线如何设计能提高效率?如何设计展厅最佳参观路线?
驻马店市第二高级中学
提出问题
建立模型
求解模型
检验结果
实际结果
课堂小结
1、感悟用数学解决实际问题的主要过程
2、了解数学建模的思想、步骤
3、通过哥尼斯堡七桥问题的数学模型感悟到数学家对人类科学发展的巨大贡献
4、学会了利用一笔画定理解决实际问题
驻马店市第二高级中学
课后作业
驻马店市第二高级中学
1、画出校园主干路图,尝试能否一笔画出.
2、观察驻马店市博物馆的结构布局,请你为参观者设计一条线路,既欣赏到所有展品,又使得走的路程最少.
3、完成课本习题8-1.
感谢观看
8.1 走近数学建模
陈琳娜
驻马店市第二高级中学
驻马店市第二高级中学
哥尼斯堡城
(今俄罗斯加里宁格勒)
康德
哥德巴赫
河上有七座桥
岛
北区
南区
东区
1
2
3
4
5
6
7
驻马店市第二高级中学
提出问题
一个步行者如何才能不重复、不遗漏、依次走完这七座桥,最后回到出发点呢?
哥尼斯堡七桥问题
驻马店市第二高级中学
莱昂哈德·欧拉(Leonhard Euler,1707年4月15日-1783年9月18日),瑞士数学家和物理学家,近代数学先驱之一。
驻马店市第二高级中学
数学抽象成排列组合问题
岛
北区
南区
东区
1
2
3
4
5
6
7
驻马店市第二高级中学
不同的走法
5040
种
驻马店市第二高级中学
实际问题的数学表述
1、岛的大小、形状影响结果吗?
2、桥的长短、宽窄影响结果吗?
不影响
不影响
驻马店市第二高级中学
陆地、桥与岛三者之间的位置关系影响结果
数学问题的解决
驻马店市第二高级中学
七桥问题数学模型
能否一笔画出此图形?
驻马店市第二高级中学
思考:“起点”、“终点”、“经过点”有什么特征?
偶点
偶点:以某一点为端点的线有偶数条
奇点:以某一点为端点的线有奇数条
驻马店市第二高级中学
一笔画定理(欧拉定理)
一个由点和线组成的图形能一笔画完,必须符合以下两个条件:
(1)图形是连在一起的,即是连通图形;
(2)图形中的奇点个数为0或2.
驻马店市第二高级中学
七桥问题中,四个点全是奇点,不能一笔画出,即不能一次无重复地走完七座桥。
用数学结论解答原问题
3
3
3
5
驻马店市第二高级中学
思考交流
1、实际问题是什么?
2、在转换成数学模型过程中,欧拉使用了哪些数学元素抽象地描述实际问题的元素?这种描述为什么不会对结果产生影响?
3、欧拉在求解模型的过程中研究出的“一笔画定理”是如何解决七桥问题的?
4、“一笔画定理”还可以用在哪些问题的解决中?
驻马店市第二高级中学
1、实际问题是:如何才能能一次无重复的走过哥尼斯堡城的七座桥,最后回到出发点。
2、在建立模型的过程中,欧拉用4个点表示被河隔开的4块陆地,用7条线表示连接陆地的七座桥,七桥问题就变成了由4个点和7条线组成的连通图形能否被一笔画出的问题,这种抽象对结果并不产生影响.起决定作用的仅是陆地、桥与岛这三者间的位置关系.
3、由一笔画定理可知连通图形中奇点个数为0个或2个。
七桥问题抽象出来的图形有4个奇点,不符合定理,不能一笔画出。
所以七座桥也不能一次不重复的走完。
4、一笔画问题在日常生活中有着广泛的应用.例如,快递员送快递怎样设计路线更省时?小区保安巡逻路线如何设计能提高效率?如何设计展厅最佳参观路线?
驻马店市第二高级中学
提出问题
建立模型
求解模型
检验结果
实际结果
数学建模
驻马店市第二高级中学
1、实际问题是:如何才能能一次无重复的走过哥尼斯堡城的七座桥,最后回到出发点。
2、在建立模型的过程中,欧拉用4个点表示被河隔开的4块陆地,用7条线表示连接陆地的七座桥,七桥问题就变成了由4个点和7条线组成的连通图形能否被一笔画出的问题,这种抽象对结果并不产生影响.起决定作用的仅是陆地、桥与岛这三者间的位置关系.
3、由一笔画定理可知连通图形中奇点个数为0个或2个。
七桥问题抽象出来的图形有4个奇点,不符合定理,不能一笔画出。
所以七座桥也不能一次不重复的走完。
4、一笔画问题在日常生活中有着广泛的应用.例如,快递员送快递怎样设计路线更省时?小区保安巡逻路线如何设计能提高效率?如何设计展厅最佳参观路线?
驻马店市第二高级中学
提出问题
建立模型
求解模型
检验结果
实际结果
课堂小结
1、感悟用数学解决实际问题的主要过程
2、了解数学建模的思想、步骤
3、通过哥尼斯堡七桥问题的数学模型感悟到数学家对人类科学发展的巨大贡献
4、学会了利用一笔画定理解决实际问题
驻马店市第二高级中学
课后作业
驻马店市第二高级中学
1、画出校园主干路图,尝试能否一笔画出.
2、观察驻马店市博物馆的结构布局,请你为参观者设计一条线路,既欣赏到所有展品,又使得走的路程最少.
3、完成课本习题8-1.
感谢观看
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
