新人教八年级级上册14.1.1同底数幂的乘法.ppt
文档属性
| 名称 | 新人教八年级级上册14.1.1同底数幂的乘法.ppt |

|
|
| 格式 | zip | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-10 23:41:59 | ||
图片预览






文档简介
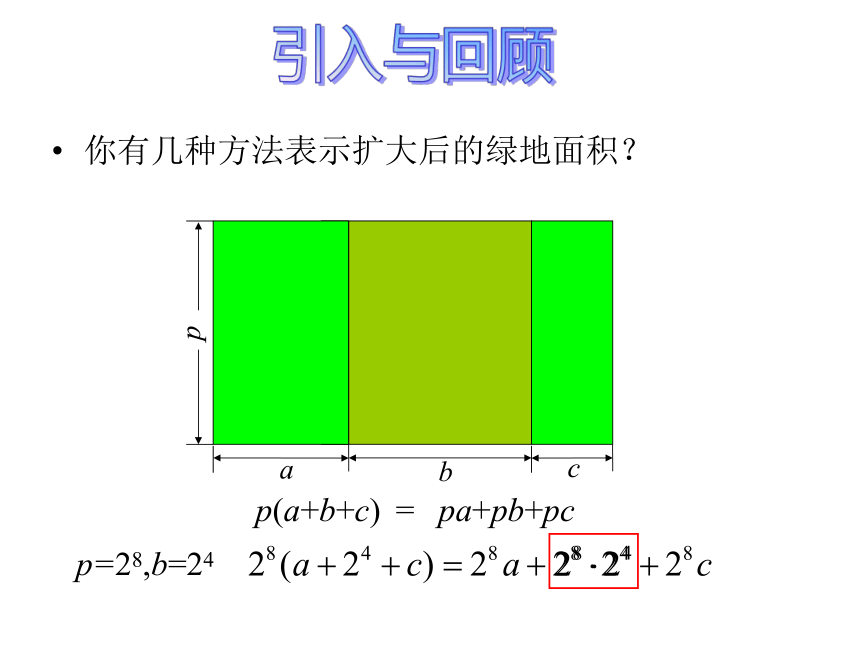
课件15张PPT。14.1.1 同底数幂的乘法第1课时你有几种方法表示扩大后的绿地面积?bacp(a+b+c)pa+pb+pc=p=28,b=24引入与回顾交流与发现根据幂的意义,计算下列各式,并用适当的方式表示结果 探究1277a72102182m+n探究23、你能用符号表示你发现的规律吗? 2、它们的积都是什么形式?积的各部分与乘数有什么关系? 1、三个乘法运算的乘数有什么共同的特征? 猜想: am · an= (当m、n都是正整数)am+n am · an =(aa…a)m个a(aa…a)n个a(乘方的意义)= aa…a(m+n)个a(乘法结合律)=am+n(乘方的意义)即am · an = am+n (当m、n都是正整数)非常好,你的猜想是正确的!交流与发现 想一想: 当三个或三个以上同底数幂相乘时,是否也 具有这一性质呢? 怎样用公式表示?同底数幂的乘法性质:am · an = am+n (m、n都是正整数) 请你尝试用文字概括这个结论。 我们可以直接利用它进行计算.同底数幂相乘,底数 ,指数 。不变相加 运算形式运算方法(同底、乘法) (底不变、指加法) 幂的底数必须相同,相乘时指数才能相加.如 43×45=43+5=48 如 am·an·ap = am+n+p (m、n、p都是正整数)例1.计算: (1)28 · 25 ;例题讲解(2)x8 · x5 ;(3)22a · 23b ;(4)x2a · x3b ;(5)(-x)8 · x5 ;(6)x8 · (- x)5 ;(7)(a-b)8 · (a-b)5 ;(8)(a-b)8 · (b-a)5 .练习1 辨一辨
判断下列计算是否正确,并简要说明理由(2) a3 +a5 = a8(3) y5 ·y4 = y20(4) x · x2 = x2(1) n3 ·n7 = n10(5) b4 · b4 = 2b4√××y9 ×x3 ×b8 课堂练习(1)x2 · x5 ;
(2)a · a6 ; (3)(-2)×(-2)4×(-2)3 ;
(4)xm · x3m+1课堂练习练习2 练一练
计算(2)已知 ,求 的值.练习3 变一变:
已知 ,用含 的代数式表示 . 例题讲解(1)在括号内用适当的正整数填空:
x6=x( )·x( ) .例2.完成下列各题 :(1)本节课学习了哪些主要内容?
(2)同底数幂的乘法运算性质是怎么探究推导出来的?在运用时要注意什么?归纳小结题型一 应用同底数幂的乘法法则进行计算课堂反馈题型二 判断并改正√×a5×x2m×课堂反馈题型三 同底数幂知识的灵活应用 (1) 可以写成( )A. B. C. D.(2)若 , 则 的值是( )A.5 B.6 C.-5 D.-6(3)若 , 则 的值是BB5课堂反馈 (2)已知 , 求a、b、c 之间的关系.(1)已知 ,求 的值. 课后思考 必做题:教科书P96,练习(2)(4),
P104,习题14.1第1(1)(2)题(2)若 , 则 . 选做题:
(1)已知 ,求 的值.布置作业
判断下列计算是否正确,并简要说明理由(2) a3 +a5 = a8(3) y5 ·y4 = y20(4) x · x2 = x2(1) n3 ·n7 = n10(5) b4 · b4 = 2b4√××y9 ×x3 ×b8 课堂练习(1)x2 · x5 ;
(2)a · a6 ; (3)(-2)×(-2)4×(-2)3 ;
(4)xm · x3m+1课堂练习练习2 练一练
计算(2)已知 ,求 的值.练习3 变一变:
已知 ,用含 的代数式表示 . 例题讲解(1)在括号内用适当的正整数填空:
x6=x( )·x( ) .例2.完成下列各题 :(1)本节课学习了哪些主要内容?
(2)同底数幂的乘法运算性质是怎么探究推导出来的?在运用时要注意什么?归纳小结题型一 应用同底数幂的乘法法则进行计算课堂反馈题型二 判断并改正√×a5×x2m×课堂反馈题型三 同底数幂知识的灵活应用 (1) 可以写成( )A. B. C. D.(2)若 , 则 的值是( )A.5 B.6 C.-5 D.-6(3)若 , 则 的值是BB5课堂反馈 (2)已知 , 求a、b、c 之间的关系.(1)已知 ,求 的值. 课后思考 必做题:教科书P96,练习(2)(4),
P104,习题14.1第1(1)(2)题(2)若 , 则 . 选做题:
(1)已知 ,求 的值.布置作业
