期末综合练习卷(试题) 小学数学四年级上册青岛版(含答案)
文档属性
| 名称 | 期末综合练习卷(试题) 小学数学四年级上册青岛版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 11:37:34 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末综合练习卷(试题)-小学数学四年级上册青岛版
一、选择题
1.用竖式计算638÷22时,把22看成20进行试商,试商结果( )。
A.偏大 B.偏小 C.正好
2.623÷89×(407-168)的运算顺序是( )。
A.-、×、÷ B.-、÷、× C.÷、×、-
3.34个15相加的和除以15的12倍,商是多少?列式为( )。
A. B. C.
4.修路时,遇到大山我们通常要开凿隧道以缩短距离,这是运用了数学上( )的道理。
A.两点确定一条直线 B.点到直线的垂直线段最短 C.两点之间线段最短
5.由6个千万,5个十万,2个万和9个一组成的数是( )。
A.60502009 B.60520009 C.65200009
6.学校篮球队员的平均身高是168厘米,最近又有一位队员参加,他的身高是176厘米,现在篮球队员的平均身高( )。
A.比168厘米高 B.比168厘米矮 C.正好168厘米
7.5厘米长的线段向两端各延长3米,得到的是一条( )。
A.直线 B.射线 C.线段
8.我们在探究“积的变化规律”和“商不变的性质”时,都经历了怎样的探究过程?( )。
A.老师直接告诉结论,我们应用结论解决问题
B.提供素材—初步发现—举例验证—总结规律
C.提供素材—举例验证—初步发现—总结规律
二、填空题
9.290265<□00265,□里最小填( );4206050>420□982,□里最大填( )。
10.在43097600这个数中,“3”在( )位上,万位上的数是( ),改写成用万作单位的数是( )万,省略万位后面的尾数约是( )万。
11.一个两位数与150相乘,积的末尾只有三个0,这个两位数最小是( ),最大是( )。
12.一个长方形水池长是50米,宽20米,在周围每隔5米种一棵树,一共种了( )棵树。现在要把水池的宽增加8米,长不变,水池的占地面积增加了( )平方米。
13.传统的十二生肖是这样一次排列的:鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2022年是虎年,那么2050年应该是( )年。
14.同一平面内,两条直线的位置关系有( )和( )。
15.两列火车分别从甲、乙两地同时相对开出,6小时后两车相遇。甲车速度是156千米/时,乙车速度是144千米/时。甲、乙两地相距( )千米。
16.把125+144÷12×8的运算顺序改变为先求商,再求和,最后求积,则原式变为( )。
三、判断题
17.A÷B=7……1,如果A和B同时扩大到原数的100倍,这时余数还是1。( )
18.如果两个乘数的末尾没有0,则积的末尾一定也没有0。( )
19.在数位顺序表中,任何两个计数单位间的进率都是10。( )
20.角的两边越长,这个角就越大。( )
21.两条直线不相交就平行。( )
四、计算题
22.直接写得数。
400×80= 230×30= 70×900= 50×140=
270÷90= 390÷13= 202×39≈ 350÷71≈
23.用竖式计算,带★要验算。
★
★
24.计算。
62+992÷(426-394) (1254-78×12)÷53 15×[12+(36-18)]
五、解答题
25.甲、乙两地相距360千米。—辆汽车从甲地开往乙地,计划8小时到达,因天气变化,实际每小时比计划少行5千米,实际多少小时到达乙地?
26.甲、乙两个工程队分别从两端开凿一条隧道。甲队每天凿8米,乙队每天凿10米,110天后凿完。求这条隧道的长。
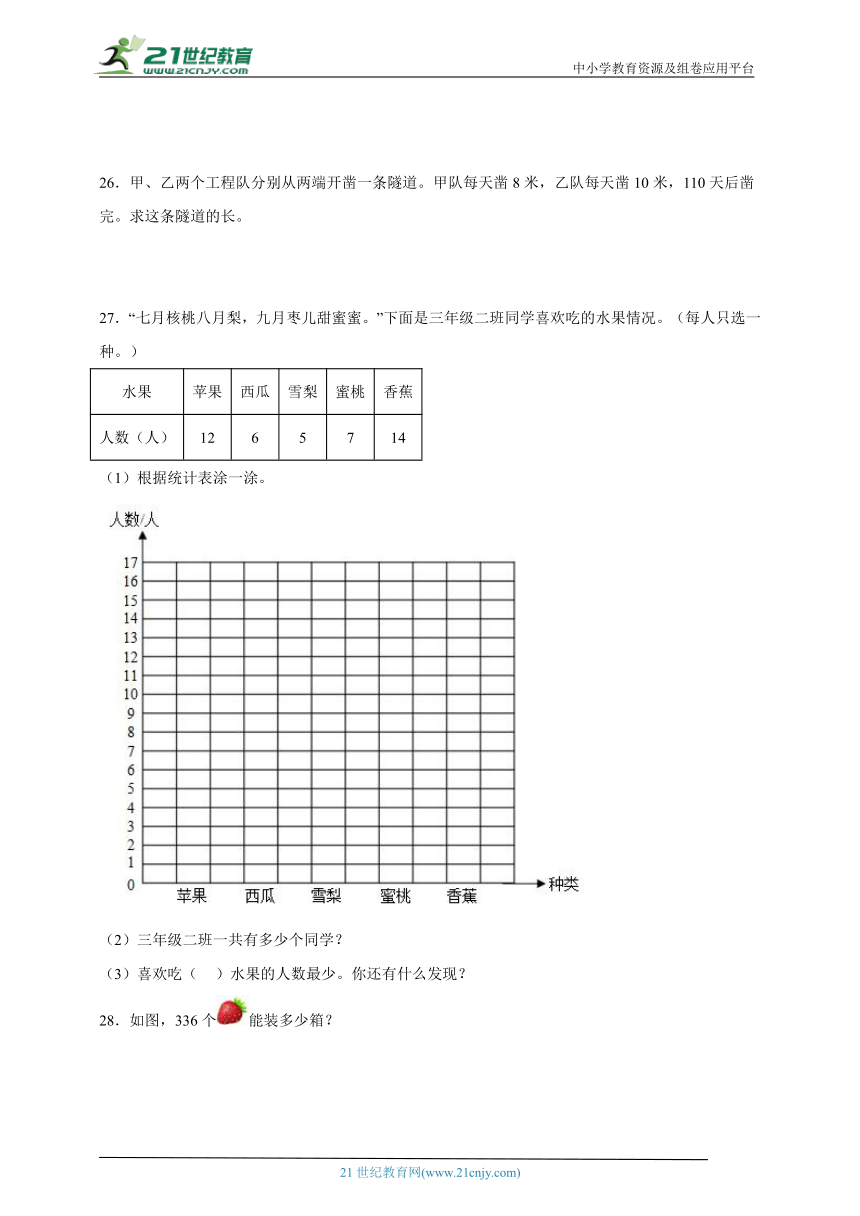
27.“七月核桃八月梨,九月枣儿甜蜜蜜。”下面是三年级二班同学喜欢吃的水果情况。(每人只选一种。)
水果 苹果 西瓜 雪梨 蜜桃 香蕉
人数(人) 12 6 5 7 14
(1)根据统计表涂一涂。
(2)三年级二班一共有多少个同学?
(3)喜欢吃( )水果的人数最少。你还有什么发现?
28.如图,336个能装多少箱?
29.小红家平均每月的水电费是203元。
(1)小红的妈妈准备了2000元来付一年的水电费,请你估一估,够吗?
(2)为倡导节约精神,小红家更换了节能水龙头和节能灯,现在平均每月水电费是154元,请你计算一下现在一年的水电费是多少钱?
30.今年学校买来72套课桌椅,学校买课桌椅花了多少元?
参考答案:
1.A
【分析】计算638÷22时,将22看成20进行试商,被除数不变,除数变小,则初商可能偏大。据此解答。
【详解】把22看成20进行试商,试商结果偏大。
故答案为:A。
【点睛】本题考查除数是两位数的试商,除数变小,初商可能偏大。除数变大,初商可能偏小。
2.B
【分析】根据整数的四则混合运算法则:有括号的先算括号里面的,然后是先乘除后加减。
【详解】根据整数的四则混合运算法则:先算小括号,再算除法,最后算乘法,
故答案为:B。
【点睛】本题考查了整数的四则混合运算,熟练掌握整数四则混合运算法则是解题的关键。
3.B
【分析】根据题意可知,要求34个15相加的和是多少,用乘法计算,本题的计算顺序是,先算15与12的积,再算15与34 的积,最后与15与34的积除以15与12的积;据此列式为:15×34÷(15×12)。
【详解】根据分析可知,
34个15相加的和除以15的12倍,商是多少?列式为15×34÷(15×12)。
故答案为:B
【点睛】熟练掌握整数四则混合运算的计算方法,是解答此题的关键。
4.C
【分析】直线上任意两点之间的一段叫做线段,连接两点的线段的长度叫做两点间的距离,两点之间,线段最短,据此即可解答。
【详解】根据分析可知,修路时,遇到大山我们通常要开凿隧道以缩短距离,这是运用了数学上两点之间线段最短的道理。
故答案为:C
【点睛】本题主要考查学生对线段的概念和特征的掌握。
5.B
【分析】整数的写法:从高位到低位,一级一级地写,哪个数位上一个单位也没有,就在那个数位上写0,据此写出整数即可。
【详解】由6个千万,5个十万,2个万和9个一组成的数是60520009。
故答案为:B
【点睛】熟练掌握整数的读写知识是解答本题的关键。
6.A
【分析】总数÷份数=平均数,据此可知,新加入的队员身高大于篮球队员的平均身高,则现在篮球队员的平均身高应比原来篮球队员的平均身高要高。据此解答。
【详解】由分析得:
现在篮球队员的平均身高比168厘米高。
故答案为:A。
【点睛】解答此题应根据平均数的意义进行分析、解答,注意新的数据大于平均数,会提高整组数据的平均数,而当新的数据小于平均数,会拉低整组数据的平均数。
7.C
【分析】把这条线段向两端各延长3米,得到的图形长6米5厘米,是有限长的。根据直线、射线和线段的特性可知,线段是有限长的,也就是可以得到一条线段。
【详解】由分析得:
5厘米长的线段向两端各延长3米,得到的是一条线段。
故答案为:C
【点睛】本题考查直线、射线和线段的特性,线段是有限长的,直线和射线都是无限长的。
8.B
【分析】由题可知,我们在探究积的变化规律和商不变的性质时,按照教材和思维逻辑,我们应先提供素材,再初步发现,然后举例验证,最后从发现中总结规律。
【详解】我们在探究积的变化规律和商不变的性质时,都经历了:提供素材—初步发现一举例验证一总结规律四个研究过程。
故答案为:B
【点睛】探究积的变化规律和商不变的性质的过程,是解答此题的关键。
9. 3 5
【分析】整数比较大小时,要看它们的位数。位数多的那个数就大;如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,下一位上的数大的那个数就大。以此类推。据此解答。
【详解】290265<□00265,两个数都是六位数,要使290265<□00265,□里面的数要比2大,□里面可以填3、4、5、6、7、8、9,□里面最小能填3;
4206050>420□982,两个数都是七位数,并且前三位数都相同,要使4206050>420□982,则□里面的数要比6小,□里面可以填5、4、3、2、1、0,□里面最大能填5。
【点睛】本题考查学生对大数比较方法的掌握。牢记大数的比较方法是解决此题的关键。
10. 百万 9 4309.76 4310
【分析】按照我国的计数习惯,从右边起,每四个数位是一级。把整万的数改写成以“万”为单位的数,就是把万位后面的0去掉,同时在后面加一个“万”字;省略万位后面的尾数就要看省略的尾数部分的最高位是小于5还是等于或大于5。小于5,把它和右面的数全部舍去,改写成0;大于或等于5,向前一位进1,再把它和右面的数全部舍去,改写成0。
【详解】在43097600这个数中,“3”在百万位上,万位上的数是9;改写成用万作单位的数是4309.76万;省略万位后面的尾数约是4310万。
【点睛】解答本题的关键是要掌握“四舍五入”法求近似数,需要强调的是数的改写时要带单位。
11. 20 80
【分析】150末尾只有一个0,150与这个两位数乘积的末尾只有3个0,则这个两位数的个位数字为0,求出100以内整十数与150的乘积,找出符合条件的最小和最大两位数,据此解答。
【详解】150×10=1500,不符合题意;
150×20=3000,符合题意;
150×30=4500,不符合题意;
150×40=6000,符合题意;
150×50=7500,不符合题意;
150×60=9000,符合题意;
150×70=10500,不符合题意;
150×80=12000,符合题意;
150×90=13500,不符合题意。
由上可知,这个两位数最小是20,最大是80。
【点睛】根据积的特征确定这个两位数的个位数字为0是解答题目的关键。
12. 28 400
【分析】根据植树问题,在封闭的图形的周围植树,相当于一端植,另一端不植的情况,也就是植树棵数等于间隔数,根据长方形周长公式:周长=(长+宽)×2,代入数据,求出长方形水池的周长,再用水池的周长除以两棵数之间的间隔距离,即可求出中植多少棵树;水池增加的面积就是一个长是50米,宽是8米的长方形的面积,根据长方形面积公式:面积=长×宽,代入数据,即可解答。
【详解】(50+20)×2÷5
=70×2÷5
=140÷5
=28(棵)
50×8=400(平方米)
【点睛】利用长方形周长公式、面积公式的应用以及植树问题进行解答,关键是熟记公式。
13.马
【分析】2050年到2022年经过2050-2022+1=29年,12年为一周期,所以29÷12=2还多5年,第一年是虎年,那么2050年是马年。
【详解】2050-2022+1=29(年)
29÷12=2(周)……5(年)
第一年是虎年,第五年是马年,即2050年是马年。
【点睛】本题主要考查周期问题和有余数除法的实际应用。
14. 相交 平行
【详解】在同一平面内的两条的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
15.1800
【分析】根据路程=速度×时间,分别求出甲车和乙车行驶的路程,再将两个路程相加,求出甲、乙两地的距离。
【详解】156×6+144×6
=936+864
=1800(千米)
则甲、乙两地相距1800千米。
【点睛】本题考查行程问题,关键是根据路程、速度和时间三者之间的关系解决问题。
16.[125+(144÷12)]×8
【分析】根据题意可知,改变后的计算顺序为先算除法,再算加法,最后算乘法,根据混合运算的计算顺序写出改变后的算式即可。
【详解】四则混合运算的计算顺序是先算乘除法,再算加减法;当有中括号时,应先算小括号里面的,再算中括号里面的,最后算中括号外面的。因此原式变为:[125+(144÷12)]×8
【点睛】熟练掌握混合运算的计算顺序是解答此题的关键。
17.×
【分析】在有余数的除法里,被除数和除数都乘相同的数或都除以相同的数(0除外),商不变,但余数也随着乘或除以相同的数,据此解答即可。
【详解】A÷B=7……1,如果A和B同时扩大到原数的100倍,这时余数也随之扩大到原来的100倍,是100。
故答案为:×
【点睛】解答本题关键是要熟练掌握商不变的性质。
18.×
【分析】例如:25乘8得200,乘数的末尾没有0,但是乘积的末尾有0,据此解答。
【详解】如果两个乘数的末尾没有0,则积的末尾可能有0,可能没有0。
故答案为:×
【点睛】熟练掌握乘数的计算方法并灵活运用是解答本题的关键。
19.×
【分析】根据数位顺序表,可知每相邻两个计数单位之间的进率都是10。
【详解】数位顺序表中,每相邻两个计数单位之间的进率都是10;不相邻的两个计数单位之间的进率不是10,例如个和百,它们的计数单位是100;整数数位顺序表中,任何两个计数单位之间的进率都是10,这种说法错误。
故答案为:×
【点睛】本题主要考查数位顺序表,注意每“相邻”两个计数单位之间的进率都是10。
20.×
【解析】略
21.×
【详解】在同一平面内的两条直线,不相交就平行,垂直是相交的特殊情况,原说法错误。
故答案为:×
22.32000;6900;63000;7000
3;30;8000;5
【解析】略
23.19600;14147
5……22;7……49
【分析】三位数乘两位数:先用第2个因数个位上的数去乘第1个因数的每一位,得数的末位和第2个因数的个位对齐;再用第2个因数十位上的数去乘第1个因数的每一位,得数的末位和第2个因数的十位对齐;然后把两次乘得的数加起来。
整数除法的计算法则:先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。如果哪一位上不够商1,要补“0”占位;每次除得的余数要小于除数。
【详解】★19600 14147
验算:
5……22 ★7……49
验算:
24.93;6;450
【分析】(1)先算小括号里面的减法,再算小括号外面的除法,最后算小括号外面的加法。
(2)先算小括号里面的乘法,再算小括号里面的减法,最后算小括号外面的除法。
(3)先算小括号里面的减法,再算中括号里面的加法,最后算中括号外面的乘法。
【详解】62+992÷(426-394)
=62+992÷32
=62+31
=93
(1254-78×12)÷53
=(1254-936)÷53
=318÷53
=6
15×[12+(36-18)]
=15×[12+18]
=15×30
=450
25.9
【分析】已知甲、乙两地相距360千米,计划时间是8小时,根据路程÷时间=速度,求出计划每小时行多少千米,减去5,求出实际每小时行驶的千米数,再根据路程÷速度=时间,代入数据,即可求出实际到达所需要的时间。
【详解】360÷(360÷8-5)
=360÷(45-5)
=360÷40
=9(小时)
答:实际9小时到达乙地。
【点睛】此题的解题关键是根据路程、时间、速度三者之间的关系,利用整数的四则混合运算,求出结果。
26.1980米
【分析】用甲队每天凿隧道长度加上乙队每天凿隧道长度,求出两队每天凿隧道长度,再乘工作天数,求出这条隧道的总长。
【详解】(8+10)×110
=18×110
=1980(米)
答:这条隧道长1980米。
【点睛】本题考查工程问题,关键是根据工作总量=工作效率×工作时间解答。
27.(1)见详解
(2)44人
(3)雪梨;喜欢吃香蕉的人数最多。(答案不唯一)
【分析】(1)整理统计表数据,填入统计图中即可。
(2)把每种水果的人数相加,即可求出共有多少个同学。
(3)观察统计图即可直接获取信息;分析统计图,只要是通过统计图数据得出的结论即可(答案不唯一,合理即可)
【详解】(1)
(2)12+6+5+7+14=44(人)
答:三年级二班一共有44个同学。
(3)观察统计图可知,喜欢吃雪梨的人数最少;我还发现喜欢吃香蕉的人数最多。(答案不唯一,合理即可)
【点睛】此题主要考查的是如何根据统计表所提供的数据绘制条形统计图、观察条形统计图并从图中获取信息,然后解决有关问题。注意绘制条形统计图时要写上标题,标上数据及绘图时间等,直条宽度相同,分布均匀,美观大方。
28.7箱
【分析】根据每盒装6个,每箱装8盒装了8个6,即6×8=48个,再据除法的意义用总的个数除以每箱装的个数即可。
【详解】6×8=48(个)
336÷48=7(箱)
答:能装7箱。
【点睛】本题的关键是根据整数乘法的意义,求出每箱装的个数,然后再根据整数除法的意义进行解答。
29.(1)不够
(2)1848元
【分析】(1)实际费用与估算费用进行比较即可解答。
(2)现在平均每月水电费乘12即等于现在一年的水电费。
【详解】(1)203>200,12>10
203×12>200×10=2000,所以不够。
答:准备2000元不够。
(2)154×12=1848(元)
答:现在一年的水电费是1848元钱。
【点睛】本题主要考查学生对整数乘法及估算方法的掌握。
30.9360元
【分析】85加45等于一套课桌椅的价钱,再乘套数即可解答。
【详解】(85+45)×72
=130×72
=9360(元)
答:学校买课桌椅花了9360元。
【点睛】先求出一套课桌椅的价钱,再作进一步解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末综合练习卷(试题)-小学数学四年级上册青岛版
一、选择题
1.用竖式计算638÷22时,把22看成20进行试商,试商结果( )。
A.偏大 B.偏小 C.正好
2.623÷89×(407-168)的运算顺序是( )。
A.-、×、÷ B.-、÷、× C.÷、×、-
3.34个15相加的和除以15的12倍,商是多少?列式为( )。
A. B. C.
4.修路时,遇到大山我们通常要开凿隧道以缩短距离,这是运用了数学上( )的道理。
A.两点确定一条直线 B.点到直线的垂直线段最短 C.两点之间线段最短
5.由6个千万,5个十万,2个万和9个一组成的数是( )。
A.60502009 B.60520009 C.65200009
6.学校篮球队员的平均身高是168厘米,最近又有一位队员参加,他的身高是176厘米,现在篮球队员的平均身高( )。
A.比168厘米高 B.比168厘米矮 C.正好168厘米
7.5厘米长的线段向两端各延长3米,得到的是一条( )。
A.直线 B.射线 C.线段
8.我们在探究“积的变化规律”和“商不变的性质”时,都经历了怎样的探究过程?( )。
A.老师直接告诉结论,我们应用结论解决问题
B.提供素材—初步发现—举例验证—总结规律
C.提供素材—举例验证—初步发现—总结规律
二、填空题
9.290265<□00265,□里最小填( );4206050>420□982,□里最大填( )。
10.在43097600这个数中,“3”在( )位上,万位上的数是( ),改写成用万作单位的数是( )万,省略万位后面的尾数约是( )万。
11.一个两位数与150相乘,积的末尾只有三个0,这个两位数最小是( ),最大是( )。
12.一个长方形水池长是50米,宽20米,在周围每隔5米种一棵树,一共种了( )棵树。现在要把水池的宽增加8米,长不变,水池的占地面积增加了( )平方米。
13.传统的十二生肖是这样一次排列的:鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪。2022年是虎年,那么2050年应该是( )年。
14.同一平面内,两条直线的位置关系有( )和( )。
15.两列火车分别从甲、乙两地同时相对开出,6小时后两车相遇。甲车速度是156千米/时,乙车速度是144千米/时。甲、乙两地相距( )千米。
16.把125+144÷12×8的运算顺序改变为先求商,再求和,最后求积,则原式变为( )。
三、判断题
17.A÷B=7……1,如果A和B同时扩大到原数的100倍,这时余数还是1。( )
18.如果两个乘数的末尾没有0,则积的末尾一定也没有0。( )
19.在数位顺序表中,任何两个计数单位间的进率都是10。( )
20.角的两边越长,这个角就越大。( )
21.两条直线不相交就平行。( )
四、计算题
22.直接写得数。
400×80= 230×30= 70×900= 50×140=
270÷90= 390÷13= 202×39≈ 350÷71≈
23.用竖式计算,带★要验算。
★
★
24.计算。
62+992÷(426-394) (1254-78×12)÷53 15×[12+(36-18)]
五、解答题
25.甲、乙两地相距360千米。—辆汽车从甲地开往乙地,计划8小时到达,因天气变化,实际每小时比计划少行5千米,实际多少小时到达乙地?
26.甲、乙两个工程队分别从两端开凿一条隧道。甲队每天凿8米,乙队每天凿10米,110天后凿完。求这条隧道的长。
27.“七月核桃八月梨,九月枣儿甜蜜蜜。”下面是三年级二班同学喜欢吃的水果情况。(每人只选一种。)
水果 苹果 西瓜 雪梨 蜜桃 香蕉
人数(人) 12 6 5 7 14
(1)根据统计表涂一涂。
(2)三年级二班一共有多少个同学?
(3)喜欢吃( )水果的人数最少。你还有什么发现?
28.如图,336个能装多少箱?
29.小红家平均每月的水电费是203元。
(1)小红的妈妈准备了2000元来付一年的水电费,请你估一估,够吗?
(2)为倡导节约精神,小红家更换了节能水龙头和节能灯,现在平均每月水电费是154元,请你计算一下现在一年的水电费是多少钱?
30.今年学校买来72套课桌椅,学校买课桌椅花了多少元?
参考答案:
1.A
【分析】计算638÷22时,将22看成20进行试商,被除数不变,除数变小,则初商可能偏大。据此解答。
【详解】把22看成20进行试商,试商结果偏大。
故答案为:A。
【点睛】本题考查除数是两位数的试商,除数变小,初商可能偏大。除数变大,初商可能偏小。
2.B
【分析】根据整数的四则混合运算法则:有括号的先算括号里面的,然后是先乘除后加减。
【详解】根据整数的四则混合运算法则:先算小括号,再算除法,最后算乘法,
故答案为:B。
【点睛】本题考查了整数的四则混合运算,熟练掌握整数四则混合运算法则是解题的关键。
3.B
【分析】根据题意可知,要求34个15相加的和是多少,用乘法计算,本题的计算顺序是,先算15与12的积,再算15与34 的积,最后与15与34的积除以15与12的积;据此列式为:15×34÷(15×12)。
【详解】根据分析可知,
34个15相加的和除以15的12倍,商是多少?列式为15×34÷(15×12)。
故答案为:B
【点睛】熟练掌握整数四则混合运算的计算方法,是解答此题的关键。
4.C
【分析】直线上任意两点之间的一段叫做线段,连接两点的线段的长度叫做两点间的距离,两点之间,线段最短,据此即可解答。
【详解】根据分析可知,修路时,遇到大山我们通常要开凿隧道以缩短距离,这是运用了数学上两点之间线段最短的道理。
故答案为:C
【点睛】本题主要考查学生对线段的概念和特征的掌握。
5.B
【分析】整数的写法:从高位到低位,一级一级地写,哪个数位上一个单位也没有,就在那个数位上写0,据此写出整数即可。
【详解】由6个千万,5个十万,2个万和9个一组成的数是60520009。
故答案为:B
【点睛】熟练掌握整数的读写知识是解答本题的关键。
6.A
【分析】总数÷份数=平均数,据此可知,新加入的队员身高大于篮球队员的平均身高,则现在篮球队员的平均身高应比原来篮球队员的平均身高要高。据此解答。
【详解】由分析得:
现在篮球队员的平均身高比168厘米高。
故答案为:A。
【点睛】解答此题应根据平均数的意义进行分析、解答,注意新的数据大于平均数,会提高整组数据的平均数,而当新的数据小于平均数,会拉低整组数据的平均数。
7.C
【分析】把这条线段向两端各延长3米,得到的图形长6米5厘米,是有限长的。根据直线、射线和线段的特性可知,线段是有限长的,也就是可以得到一条线段。
【详解】由分析得:
5厘米长的线段向两端各延长3米,得到的是一条线段。
故答案为:C
【点睛】本题考查直线、射线和线段的特性,线段是有限长的,直线和射线都是无限长的。
8.B
【分析】由题可知,我们在探究积的变化规律和商不变的性质时,按照教材和思维逻辑,我们应先提供素材,再初步发现,然后举例验证,最后从发现中总结规律。
【详解】我们在探究积的变化规律和商不变的性质时,都经历了:提供素材—初步发现一举例验证一总结规律四个研究过程。
故答案为:B
【点睛】探究积的变化规律和商不变的性质的过程,是解答此题的关键。
9. 3 5
【分析】整数比较大小时,要看它们的位数。位数多的那个数就大;如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,下一位上的数大的那个数就大。以此类推。据此解答。
【详解】290265<□00265,两个数都是六位数,要使290265<□00265,□里面的数要比2大,□里面可以填3、4、5、6、7、8、9,□里面最小能填3;
4206050>420□982,两个数都是七位数,并且前三位数都相同,要使4206050>420□982,则□里面的数要比6小,□里面可以填5、4、3、2、1、0,□里面最大能填5。
【点睛】本题考查学生对大数比较方法的掌握。牢记大数的比较方法是解决此题的关键。
10. 百万 9 4309.76 4310
【分析】按照我国的计数习惯,从右边起,每四个数位是一级。把整万的数改写成以“万”为单位的数,就是把万位后面的0去掉,同时在后面加一个“万”字;省略万位后面的尾数就要看省略的尾数部分的最高位是小于5还是等于或大于5。小于5,把它和右面的数全部舍去,改写成0;大于或等于5,向前一位进1,再把它和右面的数全部舍去,改写成0。
【详解】在43097600这个数中,“3”在百万位上,万位上的数是9;改写成用万作单位的数是4309.76万;省略万位后面的尾数约是4310万。
【点睛】解答本题的关键是要掌握“四舍五入”法求近似数,需要强调的是数的改写时要带单位。
11. 20 80
【分析】150末尾只有一个0,150与这个两位数乘积的末尾只有3个0,则这个两位数的个位数字为0,求出100以内整十数与150的乘积,找出符合条件的最小和最大两位数,据此解答。
【详解】150×10=1500,不符合题意;
150×20=3000,符合题意;
150×30=4500,不符合题意;
150×40=6000,符合题意;
150×50=7500,不符合题意;
150×60=9000,符合题意;
150×70=10500,不符合题意;
150×80=12000,符合题意;
150×90=13500,不符合题意。
由上可知,这个两位数最小是20,最大是80。
【点睛】根据积的特征确定这个两位数的个位数字为0是解答题目的关键。
12. 28 400
【分析】根据植树问题,在封闭的图形的周围植树,相当于一端植,另一端不植的情况,也就是植树棵数等于间隔数,根据长方形周长公式:周长=(长+宽)×2,代入数据,求出长方形水池的周长,再用水池的周长除以两棵数之间的间隔距离,即可求出中植多少棵树;水池增加的面积就是一个长是50米,宽是8米的长方形的面积,根据长方形面积公式:面积=长×宽,代入数据,即可解答。
【详解】(50+20)×2÷5
=70×2÷5
=140÷5
=28(棵)
50×8=400(平方米)
【点睛】利用长方形周长公式、面积公式的应用以及植树问题进行解答,关键是熟记公式。
13.马
【分析】2050年到2022年经过2050-2022+1=29年,12年为一周期,所以29÷12=2还多5年,第一年是虎年,那么2050年是马年。
【详解】2050-2022+1=29(年)
29÷12=2(周)……5(年)
第一年是虎年,第五年是马年,即2050年是马年。
【点睛】本题主要考查周期问题和有余数除法的实际应用。
14. 相交 平行
【详解】在同一平面内的两条的直线,只有两种位置关系,不是相交就是平行,垂直是相交的特殊情况。
15.1800
【分析】根据路程=速度×时间,分别求出甲车和乙车行驶的路程,再将两个路程相加,求出甲、乙两地的距离。
【详解】156×6+144×6
=936+864
=1800(千米)
则甲、乙两地相距1800千米。
【点睛】本题考查行程问题,关键是根据路程、速度和时间三者之间的关系解决问题。
16.[125+(144÷12)]×8
【分析】根据题意可知,改变后的计算顺序为先算除法,再算加法,最后算乘法,根据混合运算的计算顺序写出改变后的算式即可。
【详解】四则混合运算的计算顺序是先算乘除法,再算加减法;当有中括号时,应先算小括号里面的,再算中括号里面的,最后算中括号外面的。因此原式变为:[125+(144÷12)]×8
【点睛】熟练掌握混合运算的计算顺序是解答此题的关键。
17.×
【分析】在有余数的除法里,被除数和除数都乘相同的数或都除以相同的数(0除外),商不变,但余数也随着乘或除以相同的数,据此解答即可。
【详解】A÷B=7……1,如果A和B同时扩大到原数的100倍,这时余数也随之扩大到原来的100倍,是100。
故答案为:×
【点睛】解答本题关键是要熟练掌握商不变的性质。
18.×
【分析】例如:25乘8得200,乘数的末尾没有0,但是乘积的末尾有0,据此解答。
【详解】如果两个乘数的末尾没有0,则积的末尾可能有0,可能没有0。
故答案为:×
【点睛】熟练掌握乘数的计算方法并灵活运用是解答本题的关键。
19.×
【分析】根据数位顺序表,可知每相邻两个计数单位之间的进率都是10。
【详解】数位顺序表中,每相邻两个计数单位之间的进率都是10;不相邻的两个计数单位之间的进率不是10,例如个和百,它们的计数单位是100;整数数位顺序表中,任何两个计数单位之间的进率都是10,这种说法错误。
故答案为:×
【点睛】本题主要考查数位顺序表,注意每“相邻”两个计数单位之间的进率都是10。
20.×
【解析】略
21.×
【详解】在同一平面内的两条直线,不相交就平行,垂直是相交的特殊情况,原说法错误。
故答案为:×
22.32000;6900;63000;7000
3;30;8000;5
【解析】略
23.19600;14147
5……22;7……49
【分析】三位数乘两位数:先用第2个因数个位上的数去乘第1个因数的每一位,得数的末位和第2个因数的个位对齐;再用第2个因数十位上的数去乘第1个因数的每一位,得数的末位和第2个因数的十位对齐;然后把两次乘得的数加起来。
整数除法的计算法则:先从被除数的高位除起,除数是几位数,就看被除数的前几位;如果不够除,就多看一位,除到被除数的哪一位,商就写在哪一位的上面。如果哪一位上不够商1,要补“0”占位;每次除得的余数要小于除数。
【详解】★19600 14147
验算:
5……22 ★7……49
验算:
24.93;6;450
【分析】(1)先算小括号里面的减法,再算小括号外面的除法,最后算小括号外面的加法。
(2)先算小括号里面的乘法,再算小括号里面的减法,最后算小括号外面的除法。
(3)先算小括号里面的减法,再算中括号里面的加法,最后算中括号外面的乘法。
【详解】62+992÷(426-394)
=62+992÷32
=62+31
=93
(1254-78×12)÷53
=(1254-936)÷53
=318÷53
=6
15×[12+(36-18)]
=15×[12+18]
=15×30
=450
25.9
【分析】已知甲、乙两地相距360千米,计划时间是8小时,根据路程÷时间=速度,求出计划每小时行多少千米,减去5,求出实际每小时行驶的千米数,再根据路程÷速度=时间,代入数据,即可求出实际到达所需要的时间。
【详解】360÷(360÷8-5)
=360÷(45-5)
=360÷40
=9(小时)
答:实际9小时到达乙地。
【点睛】此题的解题关键是根据路程、时间、速度三者之间的关系,利用整数的四则混合运算,求出结果。
26.1980米
【分析】用甲队每天凿隧道长度加上乙队每天凿隧道长度,求出两队每天凿隧道长度,再乘工作天数,求出这条隧道的总长。
【详解】(8+10)×110
=18×110
=1980(米)
答:这条隧道长1980米。
【点睛】本题考查工程问题,关键是根据工作总量=工作效率×工作时间解答。
27.(1)见详解
(2)44人
(3)雪梨;喜欢吃香蕉的人数最多。(答案不唯一)
【分析】(1)整理统计表数据,填入统计图中即可。
(2)把每种水果的人数相加,即可求出共有多少个同学。
(3)观察统计图即可直接获取信息;分析统计图,只要是通过统计图数据得出的结论即可(答案不唯一,合理即可)
【详解】(1)
(2)12+6+5+7+14=44(人)
答:三年级二班一共有44个同学。
(3)观察统计图可知,喜欢吃雪梨的人数最少;我还发现喜欢吃香蕉的人数最多。(答案不唯一,合理即可)
【点睛】此题主要考查的是如何根据统计表所提供的数据绘制条形统计图、观察条形统计图并从图中获取信息,然后解决有关问题。注意绘制条形统计图时要写上标题,标上数据及绘图时间等,直条宽度相同,分布均匀,美观大方。
28.7箱
【分析】根据每盒装6个,每箱装8盒装了8个6,即6×8=48个,再据除法的意义用总的个数除以每箱装的个数即可。
【详解】6×8=48(个)
336÷48=7(箱)
答:能装7箱。
【点睛】本题的关键是根据整数乘法的意义,求出每箱装的个数,然后再根据整数除法的意义进行解答。
29.(1)不够
(2)1848元
【分析】(1)实际费用与估算费用进行比较即可解答。
(2)现在平均每月水电费乘12即等于现在一年的水电费。
【详解】(1)203>200,12>10
203×12>200×10=2000,所以不够。
答:准备2000元不够。
(2)154×12=1848(元)
答:现在一年的水电费是1848元钱。
【点睛】本题主要考查学生对整数乘法及估算方法的掌握。
30.9360元
【分析】85加45等于一套课桌椅的价钱,再乘套数即可解答。
【详解】(85+45)×72
=130×72
=9360(元)
答:学校买课桌椅花了9360元。
【点睛】先求出一套课桌椅的价钱,再作进一步解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
