2021-2022学年山东省菏泽市鄄城县七年级(上)期末数学试卷(含解析)
文档属性
| 名称 | 2021-2022学年山东省菏泽市鄄城县七年级(上)期末数学试卷(含解析) | 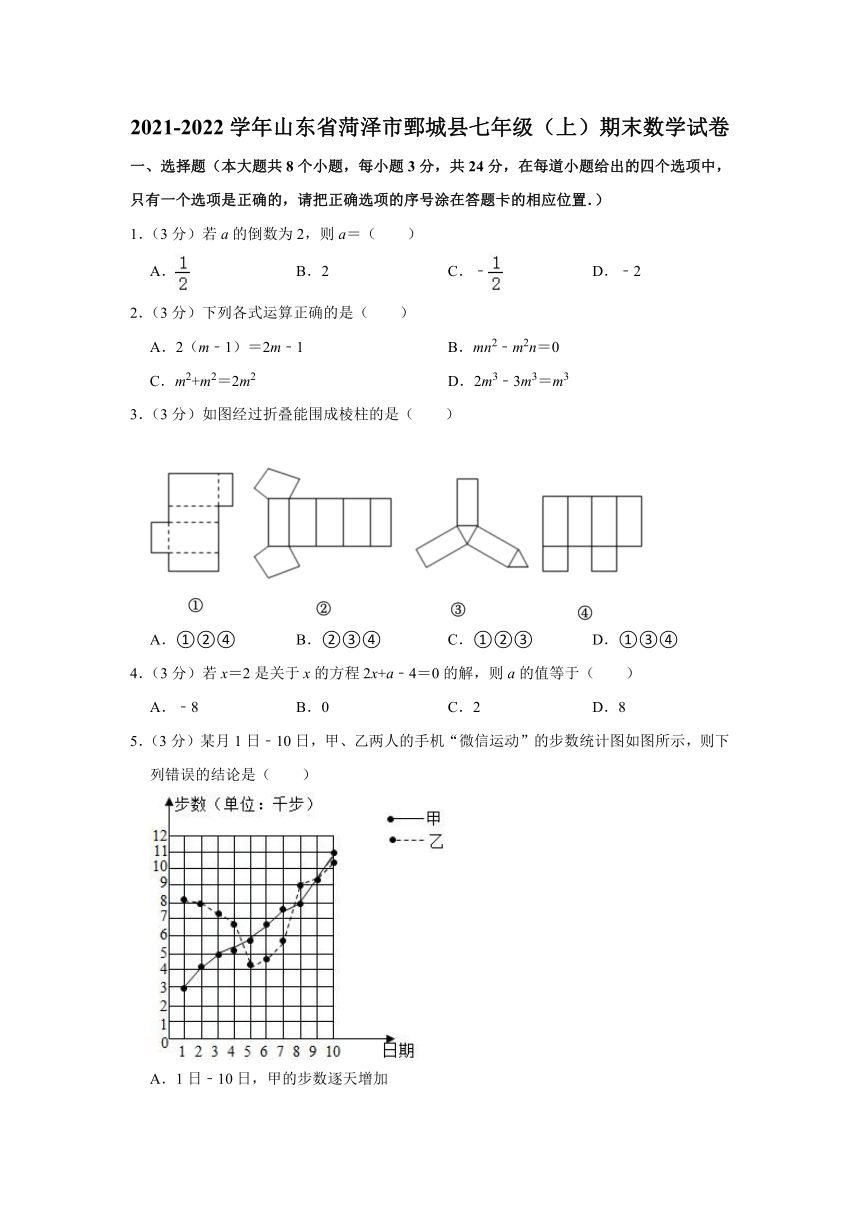 | |
| 格式 | doc | ||
| 文件大小 | 428.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 08:10:23 | ||
图片预览





文档简介
2021-2022学年山东省菏泽市鄄城县七年级(上)期末数学试卷
一、选择题(本大题共8个小题,每小题3分,共24分,在每道小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.(3分)若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
2.(3分)下列各式运算正确的是( )
A.2(m﹣1)=2m﹣1 B.mn2﹣m2n=0
C.m2+m2=2m2 D.2m3﹣3m3=m3
3.(3分)如图经过折叠能围成棱柱的是( )
A.①②④ B.②③④ C.①②③ D.①③④
4.(3分)若x=2是关于x的方程2x+a﹣4=0的解,则a的值等于( )
A.﹣8 B.0 C.2 D.8
5.(3分)某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多
6.(3分)当时钟指向晚上7:30时,时针和分针之间较小的夹角是( )
A.30° B.45° C.50° D.60°
7.(3分)若(m+2)x2|m|﹣3=5是一元一次方程,则m的值为( )
A.2 B.﹣2 C.±2 D.4
8.(3分)若线段A1A2=2,在线段A1A2的延长线上取一点A3,使A2是A1A3的中点;在线段A1A3的延长线上取一点A4,使A3是A1A4的中点;在线段A1A4的延长线上取一点A5,使A4是A1A5的中…,按这样操作下去,线段A20A21的长度为( )
A.218 B.219 C.220 D.221
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
9.(3分)2021年5月15日07时18分,我国首个火星探测器“天问一号“经过470000000公里旅程成功着陆在火星上.从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为 .
10.(3分)等于 分,1.25'等于 秒,5400″等于 度.
11.(3分)下列调查方式合适的是 .(填序号)
①要调查一批灯管的使用寿命采取普查的方式;
②了解菏泽市市民垃圾分类意识采取抽样调查方式;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人;
④发射前对“天文一号”探测器零部件的检测,采用抽样调查方式.
12.(3分)有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为a千克,再从中截出10米长的钢筋,称出这10米的质量为b千克,那么这捆钢筋的总长度为 (用含有a、b的代数式表示).
13.(3分)如图,甲从点A出发向北偏东70°的方向走到点B,乙从点A出发向南偏西15°的方向走到点C,则∠BAC的度数是 .
14.(3分)用“☆”定义一种新运算:对于任意实数a,b,都有a☆b=2a﹣3b+1.
例如:2☆1=2×2﹣3×1+1.若x☆(﹣3)=2,则x= .
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)
15.(6分)计算:
(1);
(2).
16.(6分)解下列方程:
(1)﹣2x+8=8x﹣2.
(2).
17.(6分)作图题:用尺规作图,不作法,但要保留作图痕迹
已知:线段a,b(a>b)
求作:一条线段AM,使AM=a﹣2b
18.(7分)已知A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a.
(1)求A﹣3B.
(2)求当a=2,b=﹣1时,A﹣3B的值.
19.(8分)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 名,参加剪纸的学生有 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 %;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
20.(8分)如图,O为直线AB上一点,∠AOE=126°,OF是∠AOE的平分线,∠COE是直角,求∠AOC和∠COF的度数.
21.(8分)台湾是中国领土不可分割的一部分,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的还少25万件,求北京故宫博物院约有多少万件藏品?
22.(9分)把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
23.(10分)如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6cm,BC=4cm,试求线段DE的长;
(2)如果AB=acm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,D、E分别为AC、BC的中点,试求线段DE的长度.
24.(10分)如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A、B表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
2021-2022学年山东省菏泽市鄄城县七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题3分,共24分,在每道小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.(3分)若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
【分析】根据倒数的定义:乘积是1的两数互为倒数,即可得出答案.
【解答】解:∵a的倒数为2,
∴a=.
故选:A.
2.(3分)下列各式运算正确的是( )
A.2(m﹣1)=2m﹣1 B.mn2﹣m2n=0
C.m2+m2=2m2 D.2m3﹣3m3=m3
【分析】根据去括号法则可以判断A;根据合并同类项的方法和同类项的定义可以判断B、C、D.
【解答】解:2(m﹣1)=2m﹣2,故选项A错误,不符合题意;
mmn2﹣m2n不能合并,故选项B错误,不符合题意;
m2+m2=2m2,故选项C正确,符合题意;
2m3﹣3m3=﹣m3,故选项D错误,不符合题意;
故选:C.
3.(3分)如图经过折叠能围成棱柱的是( )
A.①②④ B.②③④ C.①②③ D.①③④
【分析】根据棱柱的展开图得出结论即可.
【解答】解:由题意知,①可以围成四棱柱,②可以围成五棱柱,③可以围成三棱柱,
故选:C.
4.(3分)若x=2是关于x的方程2x+a﹣4=0的解,则a的值等于( )
A.﹣8 B.0 C.2 D.8
【分析】把x=2代入方程计算即可求出a的值,
【解答】解:把x=2代入方程得:4+a﹣4=0,
解得:a=0,
故选:B.
5.(3分)某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多
【分析】根据图中给出的甲乙两人这10天的数据,依次判断A,B,C,D选项即可.
【解答】解:A.1日﹣10日,甲的步数逐天增加;故A中结论正确,不符合题意;
B.1日﹣5日,乙的步数逐天减少;6日的步数比5日的步数多,故B中结论错误,符合题意;
C.第9日,甲、乙两人的步数正好相等;故C中结论正确,不符合题意;
D.第11日,甲的步数不一定比乙的步数多;故D中结论正确,不符合题意;
故选:B.
6.(3分)当时钟指向晚上7:30时,时针和分针之间较小的夹角是( )
A.30° B.45° C.50° D.60°
【分析】利用钟表表盘的特征解答即可.
【解答】解:7:30时,时针和分针中间相差1.5个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴7:30时分针与时针的夹角是1.5×30°=45°,
故选:B.
7.(3分)若(m+2)x2|m|﹣3=5是一元一次方程,则m的值为( )
A.2 B.﹣2 C.±2 D.4
【分析】根据一元一次方程的定义列出方程,解方程即可.
【解答】解:由题意得,2|m|﹣3=1,m+2≠0,
解得,m=2,
故选:A.
8.(3分)若线段A1A2=2,在线段A1A2的延长线上取一点A3,使A2是A1A3的中点;在线段A1A3的延长线上取一点A4,使A3是A1A4的中点;在线段A1A4的延长线上取一点A5,使A4是A1A5的中…,按这样操作下去,线段A20A21的长度为( )
A.218 B.219 C.220 D.221
【分析】利用线段中点的定义分别计算A1A3,A1A4,A1A5,…,A1An的长度,通过比较结果找到规律,依据规律解答即可得出结论.
【解答】解:∵A1A2=2,A2是A1A3的中点,
∴A1A3=2A1A2=4=22,
∵A1A3=22,A3是A1A4的中点,
∴A1A4=2A1A3=23,
∵A4是A1A5的中点,
∴A1A5=2A1A4=24,
……,
∴A1An=2n﹣1,
∴A1A21=220,
∵A20是A1A21的中点,
∴A20A21=A1A21=220=219,
故选:B.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
9.(3分)2021年5月15日07时18分,我国首个火星探测器“天问一号“经过470000000公里旅程成功着陆在火星上.从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为 4.7×108 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:470000000=4.7×108.
故答案为:4.7×108.
10.(3分)等于 24 分,1.25'等于 75 秒,5400″等于 1.5 度.
【分析】根据度分秒的进制,进行计算即可解答.
【解答】解:∵1°=60′,
∴=24′;
∵1′=60″,
∴1.25'=75″;
∵1°=3600″,
∴5400″=1.5°;
故答案为:24;75;1.5.
11.(3分)下列调查方式合适的是 ② .(填序号)
①要调查一批灯管的使用寿命采取普查的方式;
②了解菏泽市市民垃圾分类意识采取抽样调查方式;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人;
④发射前对“天文一号”探测器零部件的检测,采用抽样调查方式.
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断即可.
【解答】解:①要调查一批灯管的使用寿命,适合作抽样调查,故①不合题意;
②了解菏泽市市民垃圾分类意识,适合采取抽样调查方式,故②符合题意;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人,样本不具有代表性,故③不合题意;
④发射前对“天文一号”探测器零部件的检测,适合全面调查,故④不合题意.
故答案为:②.
12.(3分)有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为a千克,再从中截出10米长的钢筋,称出这10米的质量为b千克,那么这捆钢筋的总长度为 米 (用含有a、b的代数式表示).
【分析】根据“这10米的质量为b千克”可得1米长的钢筋质量为千克,再利用这捆钢筋的总质量除以即可解答.
【解答】解:由题意得,
1米长的钢筋质量为千克,
则这捆钢筋的总质量为:
a=(米).
故答案为:米.
13.(3分)如图,甲从点A出发向北偏东70°的方向走到点B,乙从点A出发向南偏西15°的方向走到点C,则∠BAC的度数是 125° .
【分析】首先求得AB与正东方向的夹角的度数,即可求解.
【解答】解:AB于正东方向的夹角的度数是:90°﹣70°=20°,
则∠BAC=20°+90°+15°=125°.
故答案为:125°.
14.(3分)用“☆”定义一种新运算:对于任意实数a,b,都有a☆b=2a﹣3b+1.
例如:2☆1=2×2﹣3×1+1.若x☆(﹣3)=2,则x= ﹣4 .
【分析】直接利用已知得出关于x的方程,进而得出答案.
【解答】解:由题意可得:x☆(﹣3)=2=2x﹣3×(﹣3)+1=2x+10,
解得:x=﹣4.
故答案为:﹣4.
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)
15.(6分)计算:
(1);
(2).
【分析】(1)将除法变为乘法,再根据乘法分配律计算;
(2)先算乘方,再算乘法,最后算加法;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算.
【解答】解:(1)
=(﹣+﹣)×(﹣60)
=×(﹣60)﹣×(﹣60)+×(﹣60)﹣×(﹣60)
=﹣40+6﹣10+24
=﹣20;
(2)
=﹣1﹣8×(﹣)﹣6
=﹣1+4﹣6
=﹣3.
16.(6分)解下列方程:
(1)﹣2x+8=8x﹣2.
(2).
【分析】(1)先移项,再合并同类项、x的系数化为1即可;
(2)先去分母,再去括号、移项、合并同类项、x的系数化为1即可.
【解答】解:(1)移项得,﹣2x﹣8x=﹣2﹣8,
合并同类项得,﹣10x=﹣10,
x的系数化为1得,x=1;
(2)去分母得,5(x﹣3)﹣10=2(4x+1)
去括号得,5x﹣15﹣10=8x+2,
移项得,5x﹣8x=2+15+10,
合并同类项得,﹣3x=27,
x的系数化为1得,x=﹣9.
17.(6分)作图题:用尺规作图,不作法,但要保留作图痕迹
已知:线段a,b(a>b)
求作:一条线段AM,使AM=a﹣2b
【分析】作一射线,在射线上截取AB=a,再分别截取BC=CM=b,据此可得AM=a﹣2b.
【解答】解:如图所示,AM即为所求.
18.(7分)已知A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a.
(1)求A﹣3B.
(2)求当a=2,b=﹣1时,A﹣3B的值.
【分析】(1)先把A、B表示的代数式代入,然后化简求值;
(2)把a、b的值代入化简的代数式,计算得结果.
【解答】解:(1)∵A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a,
∴A﹣3B=2a2b﹣5ab2﹣3(a2b﹣2ab2﹣a)
=2a2b﹣5ab2﹣3a2b+6ab2+3a
=﹣a2b+ab2+3a.
(2)当a=2,b=﹣1时,
A﹣3B=﹣22×(﹣1)+2×(﹣1)2+3×2
=4+2+6
=12.
19.(8分)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 50 名,参加剪纸的学生有 20 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 10 %;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
【分析】(1)根据折扇的人数和所占的百分比,求出调查的学生总人数,再用总人数减去其它课程的人数,求出剪纸的人数,从而补全统计图;
(2)用选择“陶艺”课程的学生数除以总人数即可;
(3)用八年级的总人数乘以选择“刺绣”课程的学生所占的百分比即可.
【解答】解:(1)参加问卷调查的学生人数为=50(名),
剪纸的人数有:50﹣15﹣10﹣5=20(名),
补全统计图如下:
故答案为:50,20;
(2)(2)在扇形统计图中,选择“陶艺”课程的学生所占的百分比是:×100%=10%.
故答案为:10;
(3)(名),
答:估计选择“刺绣”课程的学生有200名.
20.(8分)如图,O为直线AB上一点,∠AOE=126°,OF是∠AOE的平分线,∠COE是直角,求∠AOC和∠COF的度数.
【分析】由角平分线的定义得出∠AOF=∠EOF=∠AOE=63°,由∠COE=90°,则∠COF=∠COE﹣∠EOF=27°,∠AOC=∠AOF﹣∠COF=36°.
【解答】解:∵∠AOE=126°,OF是∠AOE的平分线,
∴∠AOF=∠EOF=∠AOE=×126°=63°,
∵∠COE是直角,
∴∠COE=90°,
∴∠COF=∠COE﹣∠EOF=90°﹣63°=27°,
∴∠AOC=∠AOF﹣∠COF=63°﹣27°=36°.
21.(8分)台湾是中国领土不可分割的一部分,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的还少25万件,求北京故宫博物院约有多少万件藏品?
【分析】先设北京故宫博物院约有x万件藏品,然后根据北京故宫博物院藏品数+台北故宫博物院藏品数=245万件,可以列出相应的方程,再求解即可
【解答】解:设北京故宫博物院约有x万件藏品,则台北故宫博物院约有(x﹣25)万件藏品.
由题意可得:x+(x﹣25)=245,
解得x=180.
答:北京故宫博物院约有180万件藏品.
22.(9分)把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 14个 小正方体?
(2)其中两面被涂到的有 4 个小正方体;没被涂到的有 1 个小正方体;
(3)求出涂上颜色部分的总面积.
【分析】(1)根据题意和图形可以得到该几何体中有多少个小正方体;
(2)根据题意和图形可以看出两面被涂到的有几个和没被涂到的有几个;
(3)根据图形可以得到涂上颜色部分的总面积.
【解答】解;(1)由图可得,
该几何体中有:1+4+9=14(个)小正方体,
故答案为:14个;
(2)由图可得,
中两面被涂到的有4个小正方体;没被涂到的有1个小正方体,
故答案为:4,1;
(3)涂上颜色部分的总面积为:1×1×(12+9+8+4)=33cm2,
即涂上颜色部分的总面积为33cm2.
23.(10分)如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6cm,BC=4cm,试求线段DE的长;
(2)如果AB=acm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,D、E分别为AC、BC的中点,试求线段DE的长度.
【分析】(1)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(3)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案.
【解答】解:(1)因为D是线段AC的中点,E是线段CB的中点,
所以DC=AC,CE=BC,
又因为AB=6cm,BC=4cm,
所以CE=2cm,DC=(AB﹣BC)=1(cm),
所以DE=DC+CE=3(cm).
(2)因为D,E是线段AC,CB的中点,
所以DC=AC,CE=BC,
所以DE=DC+CE=AC+BC=AB=a(cm).
(3)∵点D,E分别是AC,BC的中点,AC﹣BC=bcm,
∴CD=AC=(AB+BC),CE=BC,
∴DE=CD﹣CE=AC﹣BC=(AC﹣BC )=b(cm).
24.(10分)如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A、B表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
【分析】(1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②此题有两种情况:当点P在点O的左侧,点Q在点O的右侧时;当P在点O的右侧,点Q在点O的左侧时,分别画出图形进行计算即可.
【解答】解:(1)∵C表示的数为6,BC=4,
∴OB=6﹣4=2,
∴B点表示2.
∵AB=12,
∴AO=12﹣2=10,
∴A点表示﹣10;
(2)①由题意得:AP=6t,CQ=3t,如图1所示:
∵M为AP中点,
∴AM=AP=3t,
∴在数轴上点M表示的数是﹣10+3t,
∵点N在CQ上,CN=CQ,
∴CN=t,
∴在数轴上点N表示的数是6﹣t;
②如图2所示:由题意得,AP=6t,CQ=3t,分两种情况:
i)当点P在点O的左侧,点Q在点O的右侧时,OP=10﹣6t,OQ=6﹣3t,
∵O为PQ的中点,
∴OP=OQ,
∴10﹣6t=6﹣3t,
解得:t=,
当t=秒时,O为PQ的中点;
ii)当P在点O的右侧,点Q在点O的左侧时,OP=6t﹣10,OQ=3t﹣6,
∵O为PQ的中点,
∴OP=OQ,
∴6t﹣10=3t﹣6,
解得:t=,
此时AP=8<10,
∴t=不合题意舍去,
综上所述:当t=秒时,O为PQ的中点.
一、选择题(本大题共8个小题,每小题3分,共24分,在每道小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.(3分)若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
2.(3分)下列各式运算正确的是( )
A.2(m﹣1)=2m﹣1 B.mn2﹣m2n=0
C.m2+m2=2m2 D.2m3﹣3m3=m3
3.(3分)如图经过折叠能围成棱柱的是( )
A.①②④ B.②③④ C.①②③ D.①③④
4.(3分)若x=2是关于x的方程2x+a﹣4=0的解,则a的值等于( )
A.﹣8 B.0 C.2 D.8
5.(3分)某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多
6.(3分)当时钟指向晚上7:30时,时针和分针之间较小的夹角是( )
A.30° B.45° C.50° D.60°
7.(3分)若(m+2)x2|m|﹣3=5是一元一次方程,则m的值为( )
A.2 B.﹣2 C.±2 D.4
8.(3分)若线段A1A2=2,在线段A1A2的延长线上取一点A3,使A2是A1A3的中点;在线段A1A3的延长线上取一点A4,使A3是A1A4的中点;在线段A1A4的延长线上取一点A5,使A4是A1A5的中…,按这样操作下去,线段A20A21的长度为( )
A.218 B.219 C.220 D.221
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
9.(3分)2021年5月15日07时18分,我国首个火星探测器“天问一号“经过470000000公里旅程成功着陆在火星上.从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为 .
10.(3分)等于 分,1.25'等于 秒,5400″等于 度.
11.(3分)下列调查方式合适的是 .(填序号)
①要调查一批灯管的使用寿命采取普查的方式;
②了解菏泽市市民垃圾分类意识采取抽样调查方式;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人;
④发射前对“天文一号”探测器零部件的检测,采用抽样调查方式.
12.(3分)有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为a千克,再从中截出10米长的钢筋,称出这10米的质量为b千克,那么这捆钢筋的总长度为 (用含有a、b的代数式表示).
13.(3分)如图,甲从点A出发向北偏东70°的方向走到点B,乙从点A出发向南偏西15°的方向走到点C,则∠BAC的度数是 .
14.(3分)用“☆”定义一种新运算:对于任意实数a,b,都有a☆b=2a﹣3b+1.
例如:2☆1=2×2﹣3×1+1.若x☆(﹣3)=2,则x= .
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)
15.(6分)计算:
(1);
(2).
16.(6分)解下列方程:
(1)﹣2x+8=8x﹣2.
(2).
17.(6分)作图题:用尺规作图,不作法,但要保留作图痕迹
已知:线段a,b(a>b)
求作:一条线段AM,使AM=a﹣2b
18.(7分)已知A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a.
(1)求A﹣3B.
(2)求当a=2,b=﹣1时,A﹣3B的值.
19.(8分)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 名,参加剪纸的学生有 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 %;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
20.(8分)如图,O为直线AB上一点,∠AOE=126°,OF是∠AOE的平分线,∠COE是直角,求∠AOC和∠COF的度数.
21.(8分)台湾是中国领土不可分割的一部分,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的还少25万件,求北京故宫博物院约有多少万件藏品?
22.(9分)把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 小正方体?
(2)其中两面被涂到的有 个小正方体;没被涂到的有 个小正方体;
(3)求出涂上颜色部分的总面积.
23.(10分)如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6cm,BC=4cm,试求线段DE的长;
(2)如果AB=acm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,D、E分别为AC、BC的中点,试求线段DE的长度.
24.(10分)如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A、B表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
2021-2022学年山东省菏泽市鄄城县七年级(上)期末数学试卷
参考答案与试题解析
一、选择题(本大题共8个小题,每小题3分,共24分,在每道小题给出的四个选项中,只有一个选项是正确的,请把正确选项的序号涂在答题卡的相应位置.)
1.(3分)若a的倒数为2,则a=( )
A. B.2 C.﹣ D.﹣2
【分析】根据倒数的定义:乘积是1的两数互为倒数,即可得出答案.
【解答】解:∵a的倒数为2,
∴a=.
故选:A.
2.(3分)下列各式运算正确的是( )
A.2(m﹣1)=2m﹣1 B.mn2﹣m2n=0
C.m2+m2=2m2 D.2m3﹣3m3=m3
【分析】根据去括号法则可以判断A;根据合并同类项的方法和同类项的定义可以判断B、C、D.
【解答】解:2(m﹣1)=2m﹣2,故选项A错误,不符合题意;
mmn2﹣m2n不能合并,故选项B错误,不符合题意;
m2+m2=2m2,故选项C正确,符合题意;
2m3﹣3m3=﹣m3,故选项D错误,不符合题意;
故选:C.
3.(3分)如图经过折叠能围成棱柱的是( )
A.①②④ B.②③④ C.①②③ D.①③④
【分析】根据棱柱的展开图得出结论即可.
【解答】解:由题意知,①可以围成四棱柱,②可以围成五棱柱,③可以围成三棱柱,
故选:C.
4.(3分)若x=2是关于x的方程2x+a﹣4=0的解,则a的值等于( )
A.﹣8 B.0 C.2 D.8
【分析】把x=2代入方程计算即可求出a的值,
【解答】解:把x=2代入方程得:4+a﹣4=0,
解得:a=0,
故选:B.
5.(3分)某月1日﹣10日,甲、乙两人的手机“微信运动”的步数统计图如图所示,则下列错误的结论是( )
A.1日﹣10日,甲的步数逐天增加
B.1日﹣6日,乙的步数逐天减少
C.第9日,甲、乙两人的步数正好相等
D.第11日,甲的步数不一定比乙的步数多
【分析】根据图中给出的甲乙两人这10天的数据,依次判断A,B,C,D选项即可.
【解答】解:A.1日﹣10日,甲的步数逐天增加;故A中结论正确,不符合题意;
B.1日﹣5日,乙的步数逐天减少;6日的步数比5日的步数多,故B中结论错误,符合题意;
C.第9日,甲、乙两人的步数正好相等;故C中结论正确,不符合题意;
D.第11日,甲的步数不一定比乙的步数多;故D中结论正确,不符合题意;
故选:B.
6.(3分)当时钟指向晚上7:30时,时针和分针之间较小的夹角是( )
A.30° B.45° C.50° D.60°
【分析】利用钟表表盘的特征解答即可.
【解答】解:7:30时,时针和分针中间相差1.5个大格.
∵钟表12个数字,每相邻两个数字之间的夹角为30°,
∴7:30时分针与时针的夹角是1.5×30°=45°,
故选:B.
7.(3分)若(m+2)x2|m|﹣3=5是一元一次方程,则m的值为( )
A.2 B.﹣2 C.±2 D.4
【分析】根据一元一次方程的定义列出方程,解方程即可.
【解答】解:由题意得,2|m|﹣3=1,m+2≠0,
解得,m=2,
故选:A.
8.(3分)若线段A1A2=2,在线段A1A2的延长线上取一点A3,使A2是A1A3的中点;在线段A1A3的延长线上取一点A4,使A3是A1A4的中点;在线段A1A4的延长线上取一点A5,使A4是A1A5的中…,按这样操作下去,线段A20A21的长度为( )
A.218 B.219 C.220 D.221
【分析】利用线段中点的定义分别计算A1A3,A1A4,A1A5,…,A1An的长度,通过比较结果找到规律,依据规律解答即可得出结论.
【解答】解:∵A1A2=2,A2是A1A3的中点,
∴A1A3=2A1A2=4=22,
∵A1A3=22,A3是A1A4的中点,
∴A1A4=2A1A3=23,
∵A4是A1A5的中点,
∴A1A5=2A1A4=24,
……,
∴A1An=2n﹣1,
∴A1A21=220,
∵A20是A1A21的中点,
∴A20A21=A1A21=220=219,
故选:B.
二、填空题(本大题共6个小题,每小题3分,共18分,只要求把最后结果填写在答题卡的相应区域内)
9.(3分)2021年5月15日07时18分,我国首个火星探测器“天问一号“经过470000000公里旅程成功着陆在火星上.从此,火星上留下中国的脚印,同时也为我国的宇宙探测之路迈出重要一步.将470000000用科学记数法表示为 4.7×108 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:470000000=4.7×108.
故答案为:4.7×108.
10.(3分)等于 24 分,1.25'等于 75 秒,5400″等于 1.5 度.
【分析】根据度分秒的进制,进行计算即可解答.
【解答】解:∵1°=60′,
∴=24′;
∵1′=60″,
∴1.25'=75″;
∵1°=3600″,
∴5400″=1.5°;
故答案为:24;75;1.5.
11.(3分)下列调查方式合适的是 ② .(填序号)
①要调查一批灯管的使用寿命采取普查的方式;
②了解菏泽市市民垃圾分类意识采取抽样调查方式;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人;
④发射前对“天文一号”探测器零部件的检测,采用抽样调查方式.
【分析】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断即可.
【解答】解:①要调查一批灯管的使用寿命,适合作抽样调查,故①不合题意;
②了解菏泽市市民垃圾分类意识,适合采取抽样调查方式,故②符合题意;
③了解60岁以上的老人一年生病的次数在公园随机调查了30名老人,样本不具有代表性,故③不合题意;
④发射前对“天文一号”探测器零部件的检测,适合全面调查,故④不合题意.
故答案为:②.
12.(3分)有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为a千克,再从中截出10米长的钢筋,称出这10米的质量为b千克,那么这捆钢筋的总长度为 米 (用含有a、b的代数式表示).
【分析】根据“这10米的质量为b千克”可得1米长的钢筋质量为千克,再利用这捆钢筋的总质量除以即可解答.
【解答】解:由题意得,
1米长的钢筋质量为千克,
则这捆钢筋的总质量为:
a=(米).
故答案为:米.
13.(3分)如图,甲从点A出发向北偏东70°的方向走到点B,乙从点A出发向南偏西15°的方向走到点C,则∠BAC的度数是 125° .
【分析】首先求得AB与正东方向的夹角的度数,即可求解.
【解答】解:AB于正东方向的夹角的度数是:90°﹣70°=20°,
则∠BAC=20°+90°+15°=125°.
故答案为:125°.
14.(3分)用“☆”定义一种新运算:对于任意实数a,b,都有a☆b=2a﹣3b+1.
例如:2☆1=2×2﹣3×1+1.若x☆(﹣3)=2,则x= ﹣4 .
【分析】直接利用已知得出关于x的方程,进而得出答案.
【解答】解:由题意可得:x☆(﹣3)=2=2x﹣3×(﹣3)+1=2x+10,
解得:x=﹣4.
故答案为:﹣4.
三、解答题(本题共78分,把解答或证明过程写在答题卡的相应区域内)
15.(6分)计算:
(1);
(2).
【分析】(1)将除法变为乘法,再根据乘法分配律计算;
(2)先算乘方,再算乘法,最后算加法;同级运算,应按从左到右的顺序进行计算;如果有绝对值,要先做绝对值内的运算.
【解答】解:(1)
=(﹣+﹣)×(﹣60)
=×(﹣60)﹣×(﹣60)+×(﹣60)﹣×(﹣60)
=﹣40+6﹣10+24
=﹣20;
(2)
=﹣1﹣8×(﹣)﹣6
=﹣1+4﹣6
=﹣3.
16.(6分)解下列方程:
(1)﹣2x+8=8x﹣2.
(2).
【分析】(1)先移项,再合并同类项、x的系数化为1即可;
(2)先去分母,再去括号、移项、合并同类项、x的系数化为1即可.
【解答】解:(1)移项得,﹣2x﹣8x=﹣2﹣8,
合并同类项得,﹣10x=﹣10,
x的系数化为1得,x=1;
(2)去分母得,5(x﹣3)﹣10=2(4x+1)
去括号得,5x﹣15﹣10=8x+2,
移项得,5x﹣8x=2+15+10,
合并同类项得,﹣3x=27,
x的系数化为1得,x=﹣9.
17.(6分)作图题:用尺规作图,不作法,但要保留作图痕迹
已知:线段a,b(a>b)
求作:一条线段AM,使AM=a﹣2b
【分析】作一射线,在射线上截取AB=a,再分别截取BC=CM=b,据此可得AM=a﹣2b.
【解答】解:如图所示,AM即为所求.
18.(7分)已知A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a.
(1)求A﹣3B.
(2)求当a=2,b=﹣1时,A﹣3B的值.
【分析】(1)先把A、B表示的代数式代入,然后化简求值;
(2)把a、b的值代入化简的代数式,计算得结果.
【解答】解:(1)∵A=2a2b﹣5ab2,B=a2b﹣2ab2﹣a,
∴A﹣3B=2a2b﹣5ab2﹣3(a2b﹣2ab2﹣a)
=2a2b﹣5ab2﹣3a2b+6ab2+3a
=﹣a2b+ab2+3a.
(2)当a=2,b=﹣1时,
A﹣3B=﹣22×(﹣1)+2×(﹣1)2+3×2
=4+2+6
=12.
19.(8分)某学校计划在七年级开设“折扇”、“刺绣”、“剪纸”、“陶艺”四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的条形统计图和扇形统计图(部分信息未给出),其中参加折扇对应的扇形圆心角度数为108°.
请你根据以上信息解决下列问题:
(1)参加问卷调查的学生有 50 名,参加剪纸的学生有 20 名,补全条形统计图(画图并标注相应数据);
(2)在扇形统计图中,选择“陶艺”课程的学生占 10 %;
(3)若该校八年级一共有1000名学生,试估计选择“刺绣”课程的学生有多少名?
【分析】(1)根据折扇的人数和所占的百分比,求出调查的学生总人数,再用总人数减去其它课程的人数,求出剪纸的人数,从而补全统计图;
(2)用选择“陶艺”课程的学生数除以总人数即可;
(3)用八年级的总人数乘以选择“刺绣”课程的学生所占的百分比即可.
【解答】解:(1)参加问卷调查的学生人数为=50(名),
剪纸的人数有:50﹣15﹣10﹣5=20(名),
补全统计图如下:
故答案为:50,20;
(2)(2)在扇形统计图中,选择“陶艺”课程的学生所占的百分比是:×100%=10%.
故答案为:10;
(3)(名),
答:估计选择“刺绣”课程的学生有200名.
20.(8分)如图,O为直线AB上一点,∠AOE=126°,OF是∠AOE的平分线,∠COE是直角,求∠AOC和∠COF的度数.
【分析】由角平分线的定义得出∠AOF=∠EOF=∠AOE=63°,由∠COE=90°,则∠COF=∠COE﹣∠EOF=27°,∠AOC=∠AOF﹣∠COF=36°.
【解答】解:∵∠AOE=126°,OF是∠AOE的平分线,
∴∠AOF=∠EOF=∠AOE=×126°=63°,
∵∠COE是直角,
∴∠COE=90°,
∴∠COF=∠COE﹣∠EOF=90°﹣63°=27°,
∴∠AOC=∠AOF﹣∠COF=63°﹣27°=36°.
21.(8分)台湾是中国领土不可分割的一部分,在北京故宫博物院成立90周年院庆时,两岸故宫同根同源,合作举办了多项纪念活动据统计,北京故宫博物院与台北故宫博物院现共有藏品约245万件,其中台北故宫博物院藏品数量比北京故宫博物院藏品数量的还少25万件,求北京故宫博物院约有多少万件藏品?
【分析】先设北京故宫博物院约有x万件藏品,然后根据北京故宫博物院藏品数+台北故宫博物院藏品数=245万件,可以列出相应的方程,再求解即可
【解答】解:设北京故宫博物院约有x万件藏品,则台北故宫博物院约有(x﹣25)万件藏品.
由题意可得:x+(x﹣25)=245,
解得x=180.
答:北京故宫博物院约有180万件藏品.
22.(9分)把棱长为1cm的若干个小正方体摆放成如图所示的几何体,然后在露出的表面上涂上颜色(不含底面)
(1)该几何体中有 14个 小正方体?
(2)其中两面被涂到的有 4 个小正方体;没被涂到的有 1 个小正方体;
(3)求出涂上颜色部分的总面积.
【分析】(1)根据题意和图形可以得到该几何体中有多少个小正方体;
(2)根据题意和图形可以看出两面被涂到的有几个和没被涂到的有几个;
(3)根据图形可以得到涂上颜色部分的总面积.
【解答】解;(1)由图可得,
该几何体中有:1+4+9=14(个)小正方体,
故答案为:14个;
(2)由图可得,
中两面被涂到的有4个小正方体;没被涂到的有1个小正方体,
故答案为:4,1;
(3)涂上颜色部分的总面积为:1×1×(12+9+8+4)=33cm2,
即涂上颜色部分的总面积为33cm2.
23.(10分)如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6cm,BC=4cm,试求线段DE的长;
(2)如果AB=acm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,D、E分别为AC、BC的中点,试求线段DE的长度.
【分析】(1)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案;
(3)根据线段中点的性质,可得CD、CE的长,根据线段的和差,可得答案.
【解答】解:(1)因为D是线段AC的中点,E是线段CB的中点,
所以DC=AC,CE=BC,
又因为AB=6cm,BC=4cm,
所以CE=2cm,DC=(AB﹣BC)=1(cm),
所以DE=DC+CE=3(cm).
(2)因为D,E是线段AC,CB的中点,
所以DC=AC,CE=BC,
所以DE=DC+CE=AC+BC=AB=a(cm).
(3)∵点D,E分别是AC,BC的中点,AC﹣BC=bcm,
∴CD=AC=(AB+BC),CE=BC,
∴DE=CD﹣CE=AC﹣BC=(AC﹣BC )=b(cm).
24.(10分)如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
(1)写出数轴上点A、B表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒6个单位长度的速度沿数轴向右匀速运动,点Q以每秒3个单位长度的速度沿数轴向左匀速运动,M为AP的中点,点N在线段CQ上,且CN=CQ,设运动时间为t(t>0)秒.
①求数轴上点M、N表示的数(用含t的式子表示);
②t为何值时,原点O恰为线段PQ的中点.
【分析】(1)根据点C所表示的数,以及BC、AB的长度,即可写出点A、B表示的数;
(2)①根据题意画出图形,表示出AP=6t,CQ=3t,再根据线段的中点定义可得AM=3t,根据线段之间的和差关系进而可得到点M表示的数;根据CN=CQ可得CN=t,根据线段的和差关系可得到点N表示的数;
②此题有两种情况:当点P在点O的左侧,点Q在点O的右侧时;当P在点O的右侧,点Q在点O的左侧时,分别画出图形进行计算即可.
【解答】解:(1)∵C表示的数为6,BC=4,
∴OB=6﹣4=2,
∴B点表示2.
∵AB=12,
∴AO=12﹣2=10,
∴A点表示﹣10;
(2)①由题意得:AP=6t,CQ=3t,如图1所示:
∵M为AP中点,
∴AM=AP=3t,
∴在数轴上点M表示的数是﹣10+3t,
∵点N在CQ上,CN=CQ,
∴CN=t,
∴在数轴上点N表示的数是6﹣t;
②如图2所示:由题意得,AP=6t,CQ=3t,分两种情况:
i)当点P在点O的左侧,点Q在点O的右侧时,OP=10﹣6t,OQ=6﹣3t,
∵O为PQ的中点,
∴OP=OQ,
∴10﹣6t=6﹣3t,
解得:t=,
当t=秒时,O为PQ的中点;
ii)当P在点O的右侧,点Q在点O的左侧时,OP=6t﹣10,OQ=3t﹣6,
∵O为PQ的中点,
∴OP=OQ,
∴6t﹣10=3t﹣6,
解得:t=,
此时AP=8<10,
∴t=不合题意舍去,
综上所述:当t=秒时,O为PQ的中点.
同课章节目录
