2022-2023学年高一上学期数学人教A版(2019)必修第一册5.7 第2课时 三角函数的应用(二)课件(20张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册5.7 第2课时 三角函数的应用(二)课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 789.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 22:42:18 | ||
图片预览






文档简介
匀速圆周运动、简谐振动和交变电流都是理想化的运动变化现象,可以用三角函数模型准确地描述他们的运动变化规律。
在生活中也有大量运动变化现象,仅有一定范围内呈现出近似圆周变化的特点。
这些现象也可以借助三角函数近似描述。
三角函数的应用(二)
学习目标
1.通过构建三角函数模型解决生活中一些简单的问题.
2.体会三角函数是描述周期变化现象的重要函数模型.
三角函数图象类问题
一
例1
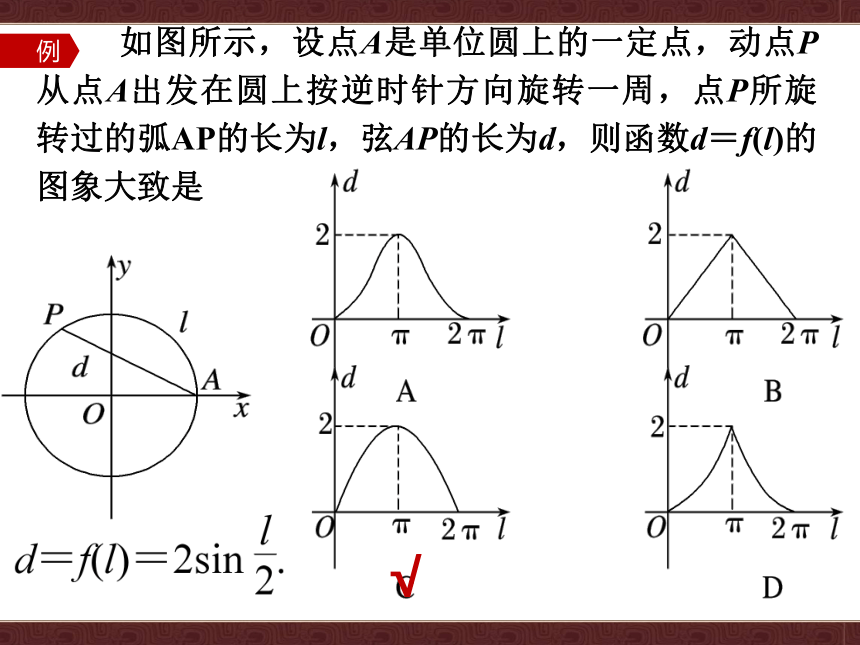
如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧AP的长为l,弦AP的长为d,则函数d=f(l)的图象大致是
√
反思感悟
解决函数图象与实际问题对应问题的策略:一般方法是根据已知所反映出来的性质解决,充分利用图象中的几何关系.此外特殊点也可以作为判断的好方法.
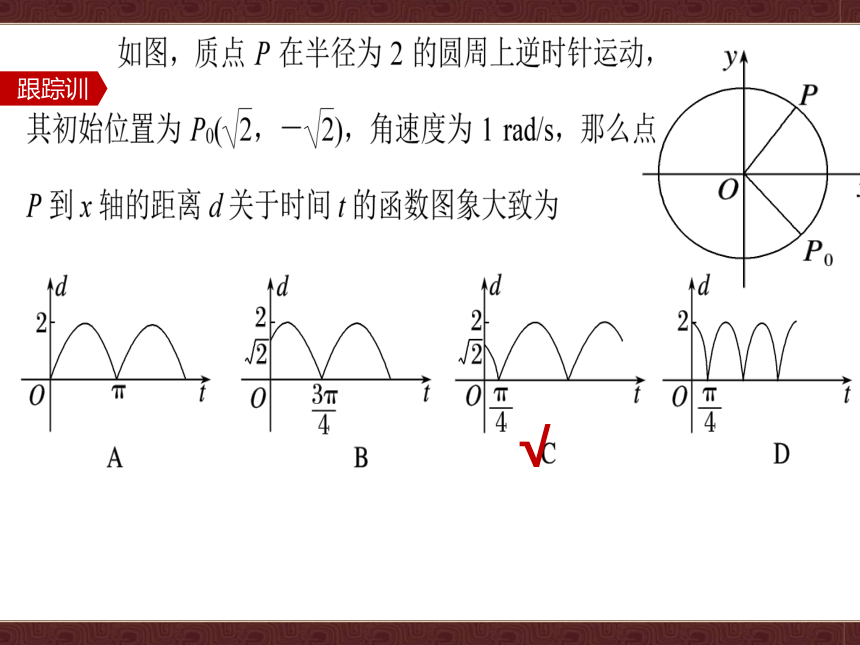
跟踪训练1
√
三角函数在生活中的应用
二
一般地,所求出的函数模型只能近似刻画这天某个时段的温度变化情况,因此应当特别注意自变量的变化范围.
反思感悟
解三角函数应用问题的基本步骤
跟踪训练2
健康成年人的收缩压和舒张压一般为120~140 mmHg和60~90 mmHg.心脏跳动时,血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.记某人的血压满足函数式p(t)=25sin 160πt+115,其中p(t)为血压(mmHg),t为时间(min),试回答下列问题:
(1)求函数p(t)的周期;
(2)求此人每分钟心跳的次数;
即此人每分钟心跳的次数为80.
(3)求出此人的血压在血压计上的读数,并与正常值比较.
p(t)max=115+25=140(mmHg),
p(t)min=115-25=90(mmHg),
即收缩压为140 mmHg,舒张压为90 mmHg.此人的血压在血压计上的读数为140/90 mmHg,在正常值范围内.
三角函数在几何中的应用
三
例3
甲同学从一个半径为r的半圆形铁板中截取一块矩形ABCD,记其最大面积为S甲,乙同学从一个半径为R的圆形铁板中截取一块矩形EFGH,记其最大面积为S乙,试问r和R满足什么关系时,S甲=S乙?说明理由.
如图所示,甲图中,O是半圆圆心,设∠COD=θ,
则CD=rsin θ,OC=rcos θ,
S矩形ABCD=2OC·CD
=2rcos θ·rsin θ=r2sin 2θ,
乙图中,设∠EGF=α,则EF=2Rsin α,则FG=2Rcos α,
S矩形EFGH=EF·FG=2Rcos α·2Rsin α=2R2sin 2α,
反思感悟
利用三角函数解决几何问题,首先要审清题意,然后要明确角的取值范围,最后一定要回归到实际问题当中去.
跟踪训练3
如图,在矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为___________.
则PM=1-sin α,PN=2-cos α,
周长C=6-2(sin α+cos α)
=6 - ????????????????????(∝+????????)
又????≤∝则 ????????≤∝+?????????
课堂
小结
1.知识清单:
(1)三角函数在生活中的应用.
(2)三角函数在几何中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际问题.
在生活中也有大量运动变化现象,仅有一定范围内呈现出近似圆周变化的特点。
这些现象也可以借助三角函数近似描述。
三角函数的应用(二)
学习目标
1.通过构建三角函数模型解决生活中一些简单的问题.
2.体会三角函数是描述周期变化现象的重要函数模型.
三角函数图象类问题
一
例1
如图所示,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧AP的长为l,弦AP的长为d,则函数d=f(l)的图象大致是
√
反思感悟
解决函数图象与实际问题对应问题的策略:一般方法是根据已知所反映出来的性质解决,充分利用图象中的几何关系.此外特殊点也可以作为判断的好方法.
跟踪训练1
√
三角函数在生活中的应用
二
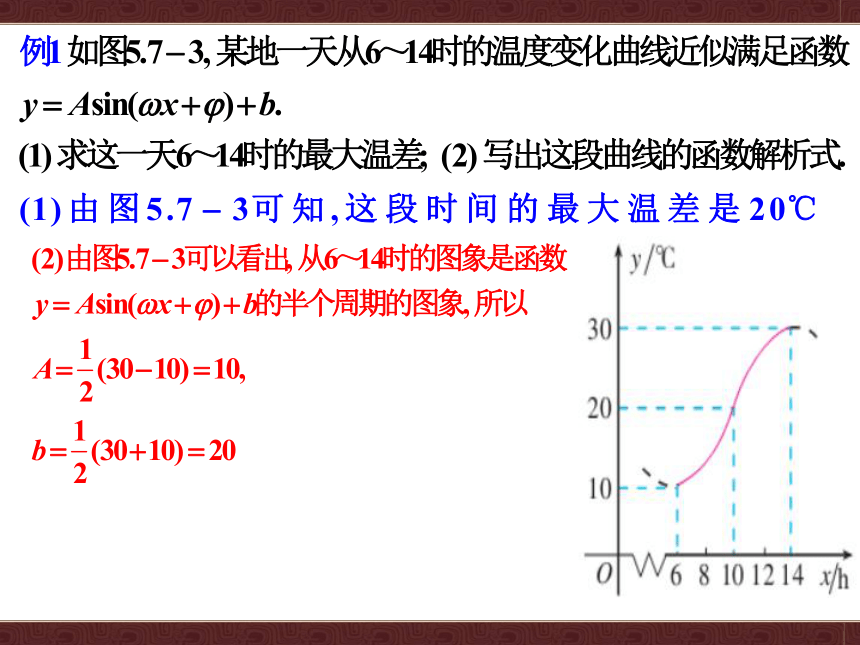
一般地,所求出的函数模型只能近似刻画这天某个时段的温度变化情况,因此应当特别注意自变量的变化范围.
反思感悟
解三角函数应用问题的基本步骤
跟踪训练2
健康成年人的收缩压和舒张压一般为120~140 mmHg和60~90 mmHg.心脏跳动时,血压在增加或减小.血压的最大值、最小值分别称为收缩压和舒张压,血压计上的读数就是收缩压和舒张压,读数120/80 mmHg为标准值.记某人的血压满足函数式p(t)=25sin 160πt+115,其中p(t)为血压(mmHg),t为时间(min),试回答下列问题:
(1)求函数p(t)的周期;
(2)求此人每分钟心跳的次数;
即此人每分钟心跳的次数为80.
(3)求出此人的血压在血压计上的读数,并与正常值比较.
p(t)max=115+25=140(mmHg),
p(t)min=115-25=90(mmHg),
即收缩压为140 mmHg,舒张压为90 mmHg.此人的血压在血压计上的读数为140/90 mmHg,在正常值范围内.
三角函数在几何中的应用
三
例3
甲同学从一个半径为r的半圆形铁板中截取一块矩形ABCD,记其最大面积为S甲,乙同学从一个半径为R的圆形铁板中截取一块矩形EFGH,记其最大面积为S乙,试问r和R满足什么关系时,S甲=S乙?说明理由.
如图所示,甲图中,O是半圆圆心,设∠COD=θ,
则CD=rsin θ,OC=rcos θ,
S矩形ABCD=2OC·CD
=2rcos θ·rsin θ=r2sin 2θ,
乙图中,设∠EGF=α,则EF=2Rsin α,则FG=2Rcos α,
S矩形EFGH=EF·FG=2Rcos α·2Rsin α=2R2sin 2α,
反思感悟
利用三角函数解决几何问题,首先要审清题意,然后要明确角的取值范围,最后一定要回归到实际问题当中去.
跟踪训练3
如图,在矩形OABC中,AB=1,OA=2,以B为圆心、BA为半径在矩形内部作弧,点P是弧上一动点,PM⊥OA,垂足为M,PN⊥OC,垂足为N,则四边形OMPN的周长的最小值为___________.
则PM=1-sin α,PN=2-cos α,
周长C=6-2(sin α+cos α)
=6 - ????????????????????(∝+????????)
又????≤∝则 ????????≤∝+?????????
课堂
小结
1.知识清单:
(1)三角函数在生活中的应用.
(2)三角函数在几何中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际问题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
