2013---2014学年度上学期数学期末质量检测模拟试题(青岛版)(附答案)
文档属性
| 名称 | 2013---2014学年度上学期数学期末质量检测模拟试题(青岛版)(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 210.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-10 16:10:19 | ||
图片预览


文档简介
2013-2014学年九年级数学期末考试模拟试题
一.选择题(共16小题)
1.(2013 营口)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
2.(2013 雅安)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.
A.2 B. 3 C. 4 D. 5
(2) (3) (4) (5)
3.(2013 曲靖)如图,在 ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A. 梯形 B. 矩形 C. 菱形 D. 正方形
4.(2013 玉溪)如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A. 30° B. 45° C. 90° D. 135°
5.(2013 烟台)如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
A. (6,1) B. (0,1) C. (0,﹣3) D. (6,﹣3)
6.(2013 泸州)若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A. k>﹣1 B.k<1且k≠0 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
7.(2013 铜仁地区)⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
A. 相切 B. 相交 C. 相离 D. 不能确定
8.(2013 柳州)下列四个图中,∠x是圆周角的是( )
A. B. C. D.
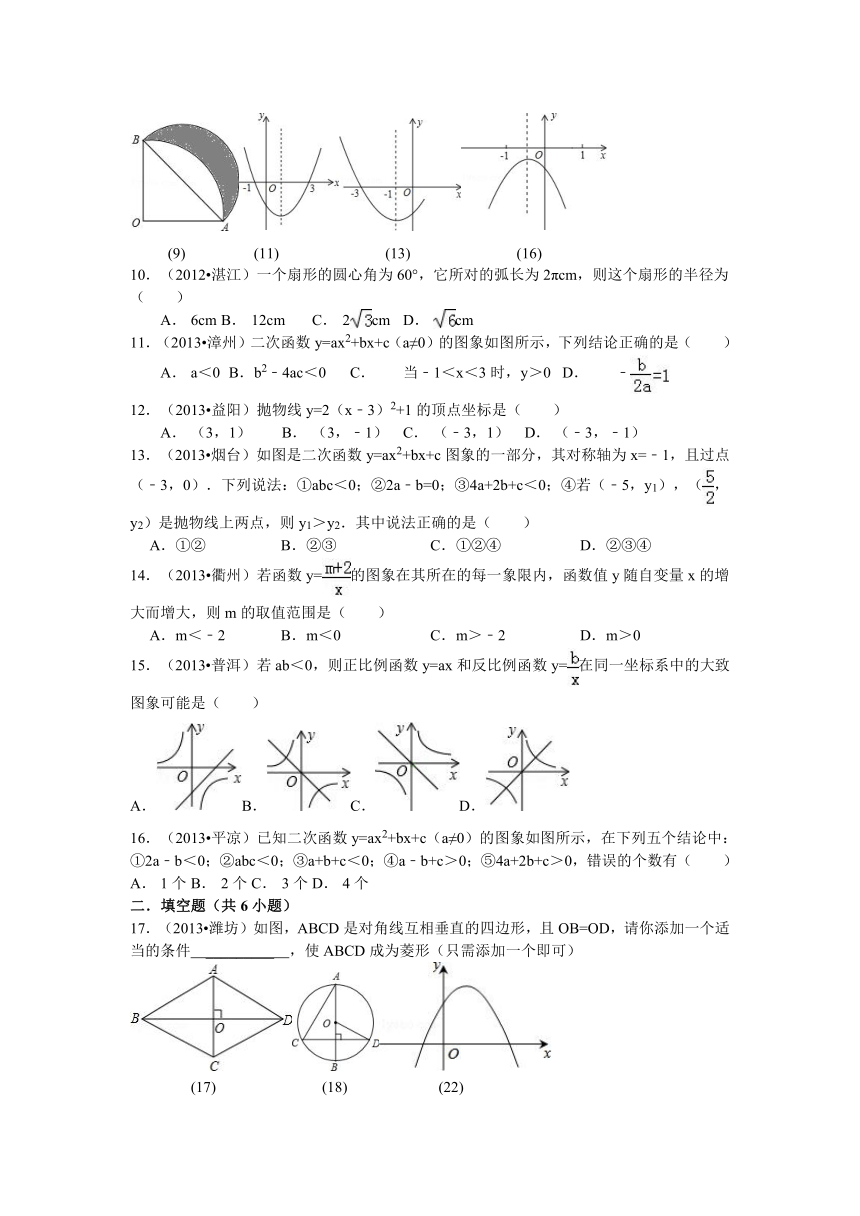
9.(2013 德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A. B. C. D.
(9) (11) (13) (16)
10.(2012 湛江)一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为( )
A. 6cm B. 12cm C. 2cm D. cm
11.(2013 漳州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
A. a<0 B.b2﹣4ac<0 C. 当﹣1<x<3时,y>0 D. ﹣
12.(2013 益阳)抛物线y=2(x﹣3)2+1的顶点坐标是( )
A. (3,1) B. (3,﹣1) C. (﹣3,1) D. (﹣3,﹣1)
13.(2013 烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A.①② B. ②③ C. ①②④ D. ②③④
14.(2013 衢州)若函数y=的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
A.m<﹣2 B. m<0 C. m>﹣2 D. m>0
15.(2013 普洱)若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
A.B.C.D.
16.(2013 平凉)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,错误的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
二.填空题(共6小题)
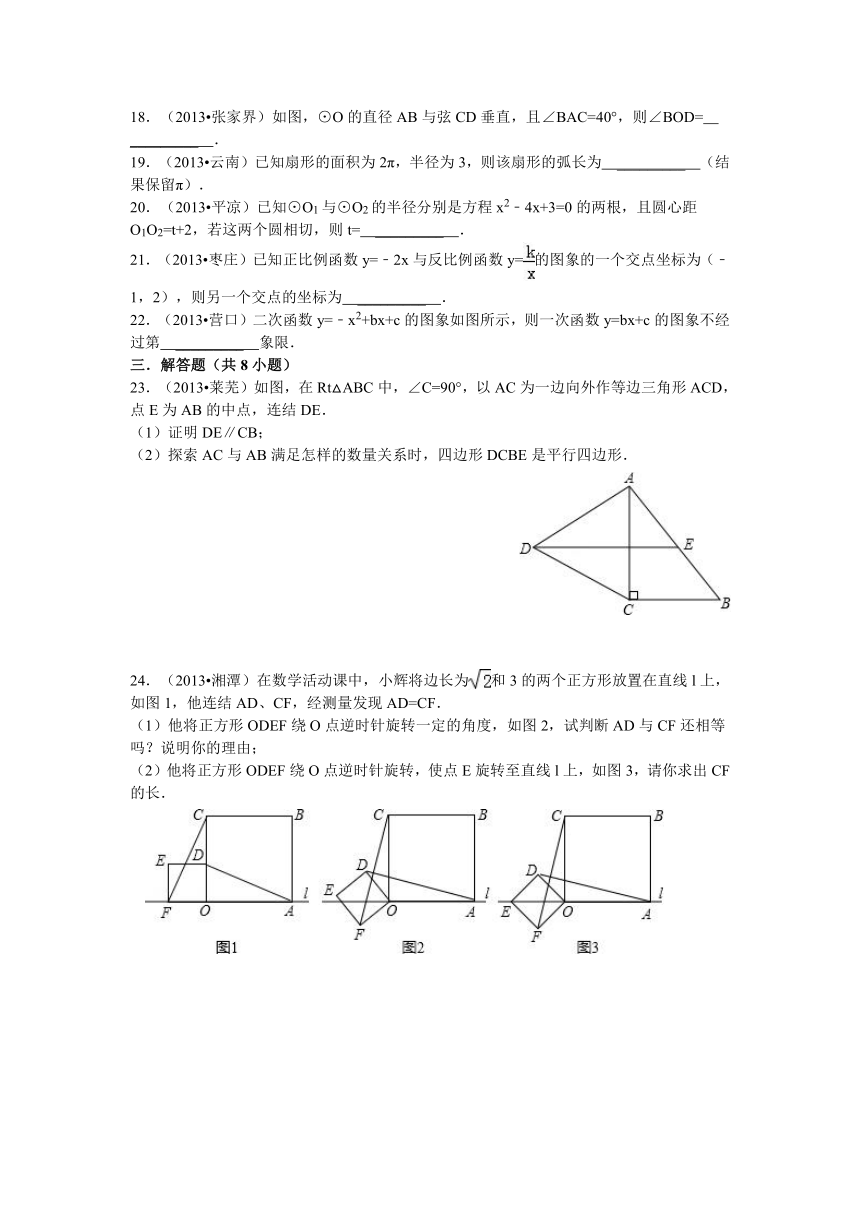
17.(2013 潍坊)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 _________ ,使ABCD成为菱形(只需添加一个即可)
(17) (18) (22)
18.(2013 张家界)如图,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD= _________ .
19.(2013 云南)已知扇形的面积为2π,半径为3,则该扇形的弧长为 _________ (结果保留π).
20.(2013 平凉)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t= _________ .
21.(2013 枣庄)已知正比例函数y=﹣2x与反比例函数y=的图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为 _________ .
22.(2013 营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第 _________ 象限.
三.解答题(共8小题)
23.(2013 莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
24.(2013 湘潭)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
25.(2012 山西)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
26.(2013 钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
27.(2013 东营)如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
28.(2013 营口)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
29.(2013 湘西州)如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=的图象有一个交点A(m,2).
(1)求m的值;
(2)求正比例函数y=kx的解析式;
(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
30.(2013 铜仁地区)如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
2013-2014学年九年级数学期末考试模拟试题
参考答案与试题解析
一.选择题(共16小题)
1.A2.C3.C4.C5.B6.D7.B8.C9.C10.A11.D 12.A13.C14.A15.C16.B
二.填空题(共6小题)
17. OA=OC 18. 80° .19. 20. 2或0 .21.(1,﹣2) .22. 四 .
三.解答题(共8小题)
23.解答: (1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD.
在△ADE与△CDE中,,∴△ADE≌△CDE(SSS),∴∠ADE=∠CDE=30°.
∵∠DCB=150°,∴∠EDC+∠DCB=180°.∴DE∥CB.
(2)解:∵∠DCB=150°,若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.
∴∠B=30°.
在Rt△ACB中,sinB=,sin30°==,AC=或AB=2AC.
∴当AC=或AB=2AC时,四边形DCBE是平行四边形.
24. 解答: 解:(1)AD=CF.
理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF,
在△AOD和△COF中,,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,
如图,连接DF交OE于G,则DF⊥OE,DG=OG=OE,
∵正方形ODEF的边长为,∴OE=×=2,
∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4,
在Rt△ADG中,AD===,
∴CF=AD=.
25.解答:(1)解:设每千克核桃应降价x元.
根据题意,得 (60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),
答:该店应按原售价的九折出售. …10分
26. 解答: 解:(1)∵AB与圆O相切,∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,∴AD∥EO,
∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AC为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=×2×3+×3×4.5﹣=3+﹣=.
27. 解答: 解:(1)直线CD与⊙O相切.
理由如下:连接OC.∵OA=OC,∴∠BAC=∠OCA,
∵∠BAC=∠CAM,∴∠OCA=∠CAM,∴OC∥AM,
∵CD⊥AM,∴OC⊥CD,∵OC为半径,
∴直线CD与⊙O相切.
(2)∵OC=OA,∴∠BAC=∠ACO,
∵∠CAB=30°,∴∠COE=2∠CAB=60°,∴在Rt△COE中,OC=3,CE=OC tan60°=.
28. 解答: 解:(1)由题意得出:w=(x﹣20) y=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600,
故w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程﹣2(x﹣30)2+200=150.
解得 x1=25,x2=35.
∵35>28,
∴x2=35不符合题意,应舍去.
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
29. 解答: 解:(1)∵反比例函数y=的图象过点A(m,2),∴2=,解得m=1;
(2)∵正比例函数y=kx的图象过点A(1,2),∴2=k×1,解得k=2,
∴正比例函数解析式为y=2x;
(3)点B(2,3)不在正比例函数图象上,理由如下:
将x=2代入y=2x,得y=2×2=4≠3,
所以点B(2,3)不在正比例函数y=2x的图象上.
30. 解答: 解:(1)∵直线y=3x﹣3分别交x轴、y轴于A、B两点,
∴可得A(1,0),B(0,﹣3),
把A、B两点的坐标分别代入y=x2+bx+c得:,解得:.
∴抛物线解析式为:y=x2+2x﹣3.
(2)令y=0得:0=x2+2x﹣3,解得:x1=1,x2=﹣3,则C点坐标为:(﹣3,0),AC=4,
故可得S△ABC=AC×OB=×4×3=6.
(3)抛物线的对称轴为:x=﹣1,假设存在M(﹣1,m)满足题意:
讨论:
①当MA=AB时,,解得:,
∴M1(﹣1,),M2(﹣1,﹣);
②当MB=BA时,,解得:M3=0,M4=﹣6,
∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去),
③当MB=MA时,,解得:m=﹣1,
∴M5(﹣1,﹣1),
答:共存在4个点M1(﹣1,),M2(﹣1,﹣),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.
一.选择题(共16小题)
1.(2013 营口)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.B.C.D.
2.(2013 雅安)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.
A.2 B. 3 C. 4 D. 5
(2) (3) (4) (5)
3.(2013 曲靖)如图,在 ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A. 梯形 B. 矩形 C. 菱形 D. 正方形
4.(2013 玉溪)如图,点A、B、C、D都在方格纸的格点上,若△AOB绕点O按逆时针方向旋转到△COD的位置,则旋转的角度为( )
A. 30° B. 45° C. 90° D. 135°
5.(2013 烟台)如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A′的坐标是( )
A. (6,1) B. (0,1) C. (0,﹣3) D. (6,﹣3)
6.(2013 泸州)若关于x的一元二次方程kx2﹣2x﹣1=0有两个不相等的实数根,则实数k的取值范围是( )
A. k>﹣1 B.k<1且k≠0 C.k≥﹣1且k≠0 D.k>﹣1且k≠0
7.(2013 铜仁地区)⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
A. 相切 B. 相交 C. 相离 D. 不能确定
8.(2013 柳州)下列四个图中,∠x是圆周角的是( )
A. B. C. D.
9.(2013 德州)如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中阴影部分的面积为( )
A. B. C. D.
(9) (11) (13) (16)
10.(2012 湛江)一个扇形的圆心角为60°,它所对的弧长为2πcm,则这个扇形的半径为( )
A. 6cm B. 12cm C. 2cm D. cm
11.(2013 漳州)二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论正确的是( )
A. a<0 B.b2﹣4ac<0 C. 当﹣1<x<3时,y>0 D. ﹣
12.(2013 益阳)抛物线y=2(x﹣3)2+1的顶点坐标是( )
A. (3,1) B. (3,﹣1) C. (﹣3,1) D. (﹣3,﹣1)
13.(2013 烟台)如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(,y2)是抛物线上两点,则y1>y2.其中说法正确的是( )
A.①② B. ②③ C. ①②④ D. ②③④
14.(2013 衢州)若函数y=的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
A.m<﹣2 B. m<0 C. m>﹣2 D. m>0
15.(2013 普洱)若ab<0,则正比例函数y=ax和反比例函数y=在同一坐标系中的大致图象可能是( )
A.B.C.D.
16.(2013 平凉)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:
①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,错误的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
二.填空题(共6小题)
17.(2013 潍坊)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 _________ ,使ABCD成为菱形(只需添加一个即可)
(17) (18) (22)
18.(2013 张家界)如图,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD= _________ .
19.(2013 云南)已知扇形的面积为2π,半径为3,则该扇形的弧长为 _________ (结果保留π).
20.(2013 平凉)已知⊙O1与⊙O2的半径分别是方程x2﹣4x+3=0的两根,且圆心距O1O2=t+2,若这两个圆相切,则t= _________ .
21.(2013 枣庄)已知正比例函数y=﹣2x与反比例函数y=的图象的一个交点坐标为(﹣1,2),则另一个交点的坐标为 _________ .
22.(2013 营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第 _________ 象限.
三.解答题(共8小题)
23.(2013 莱芜)如图,在Rt△ABC中,∠C=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE.
(1)证明DE∥CB;
(2)探索AC与AB满足怎样的数量关系时,四边形DCBE是平行四边形.
24.(2013 湘潭)在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.
25.(2012 山西)山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
26.(2013 钦州)如图,在Rt△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆与AB边相切于点D,与AC、BC边分别交于点E、F、G,连接OD,已知BD=2,AE=3,tan∠BOD=.
(1)求⊙O的半径OD;
(2)求证:AE是⊙O的切线;
(3)求图中两部分阴影面积的和.
27.(2013 东营)如图,AB为⊙O的直径,点C为⊙O上一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若直线l与AB的延长线相交于点E,⊙O的半径为3,并且∠CAB=30°,求CE的长.
28.(2013 营口)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
29.(2013 湘西州)如图,在平面直角坐标系xOy中,正比例函数y=kx的图象与反比例函数y=的图象有一个交点A(m,2).
(1)求m的值;
(2)求正比例函数y=kx的解析式;
(3)试判断点B(2,3)是否在正比例函数图象上,并说明理由.
30.(2013 铜仁地区)如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
2013-2014学年九年级数学期末考试模拟试题
参考答案与试题解析
一.选择题(共16小题)
1.A2.C3.C4.C5.B6.D7.B8.C9.C10.A11.D 12.A13.C14.A15.C16.B
二.填空题(共6小题)
17. OA=OC 18. 80° .19. 20. 2或0 .21.(1,﹣2) .22. 四 .
三.解答题(共8小题)
23.解答: (1)证明:连结CE.
∵点E为Rt△ACB的斜边AB的中点,∴CE=AB=AE.
∵△ACD是等边三角形,∴AD=CD.
在△ADE与△CDE中,,∴△ADE≌△CDE(SSS),∴∠ADE=∠CDE=30°.
∵∠DCB=150°,∴∠EDC+∠DCB=180°.∴DE∥CB.
(2)解:∵∠DCB=150°,若四边形DCBE是平行四边形,则DC∥BE,∠DCB+∠B=180°.
∴∠B=30°.
在Rt△ACB中,sinB=,sin30°==,AC=或AB=2AC.
∴当AC=或AB=2AC时,四边形DCBE是平行四边形.
24. 解答: 解:(1)AD=CF.
理由如下:在正方形ABCO和正方形ODEF中,AO=CO,OD=OF,∠AOC=∠DOF=90°,
∴∠AOC+∠COD=∠DOF+∠COD,即∠AOD=∠COF,
在△AOD和△COF中,,∴△AOD≌△COF(SAS),∴AD=CF;
(2)与(1)同理求出CF=AD,
如图,连接DF交OE于G,则DF⊥OE,DG=OG=OE,
∵正方形ODEF的边长为,∴OE=×=2,
∴DG=OG=OE=×2=1,∴AG=AO+OG=3+1=4,
在Rt△ADG中,AD===,
∴CF=AD=.
25.解答:(1)解:设每千克核桃应降价x元.
根据题意,得 (60﹣x﹣40)(100+×20)=2240.
化简,得 x2﹣10x+24=0 解得x1=4,x2=6.
答:每千克核桃应降价4元或6元.
(2)解:由(1)可知每千克核桃可降价4元或6元.
因为要尽可能让利于顾客,所以每千克核桃应降价6元.
此时,售价为:60﹣6=54(元),
答:该店应按原售价的九折出售. …10分
26. 解答: 解:(1)∵AB与圆O相切,∴OD⊥AB,
在Rt△BDO中,BD=2,tan∠BOD==,∴OD=3;
(2)连接OE,∵AE=OD=3,AE∥OD,∴四边形AEOD为平行四边形,∴AD∥EO,
∵DA⊥AE,∴OE⊥AC,又∵OE为圆的半径,∴AC为圆O的切线;
(3)∵OD∥AC,∴=,即=,∴AC=7.5,∴EC=AC﹣AE=7.5﹣3=4.5,
∴S阴影=S△BDO+S△OEC﹣S扇形FOD﹣S扇形EOG
=×2×3+×3×4.5﹣=3+﹣=.
27. 解答: 解:(1)直线CD与⊙O相切.
理由如下:连接OC.∵OA=OC,∴∠BAC=∠OCA,
∵∠BAC=∠CAM,∴∠OCA=∠CAM,∴OC∥AM,
∵CD⊥AM,∴OC⊥CD,∵OC为半径,
∴直线CD与⊙O相切.
(2)∵OC=OA,∴∠BAC=∠ACO,
∵∠CAB=30°,∴∠COE=2∠CAB=60°,∴在Rt△COE中,OC=3,CE=OC tan60°=.
28. 解答: 解:(1)由题意得出:w=(x﹣20) y=(x﹣20)(﹣2x+80)=﹣2x2+120x﹣1600,
故w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润200元.
(3)当w=150时,可得方程﹣2(x﹣30)2+200=150.
解得 x1=25,x2=35.
∵35>28,
∴x2=35不符合题意,应舍去.
答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.
29. 解答: 解:(1)∵反比例函数y=的图象过点A(m,2),∴2=,解得m=1;
(2)∵正比例函数y=kx的图象过点A(1,2),∴2=k×1,解得k=2,
∴正比例函数解析式为y=2x;
(3)点B(2,3)不在正比例函数图象上,理由如下:
将x=2代入y=2x,得y=2×2=4≠3,
所以点B(2,3)不在正比例函数y=2x的图象上.
30. 解答: 解:(1)∵直线y=3x﹣3分别交x轴、y轴于A、B两点,
∴可得A(1,0),B(0,﹣3),
把A、B两点的坐标分别代入y=x2+bx+c得:,解得:.
∴抛物线解析式为:y=x2+2x﹣3.
(2)令y=0得:0=x2+2x﹣3,解得:x1=1,x2=﹣3,则C点坐标为:(﹣3,0),AC=4,
故可得S△ABC=AC×OB=×4×3=6.
(3)抛物线的对称轴为:x=﹣1,假设存在M(﹣1,m)满足题意:
讨论:
①当MA=AB时,,解得:,
∴M1(﹣1,),M2(﹣1,﹣);
②当MB=BA时,,解得:M3=0,M4=﹣6,
∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去),
③当MB=MA时,,解得:m=﹣1,
∴M5(﹣1,﹣1),
答:共存在4个点M1(﹣1,),M2(﹣1,﹣),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.
同课章节目录
